45 Is 30 Of What Number
faraar
Sep 20, 2025 · 6 min read
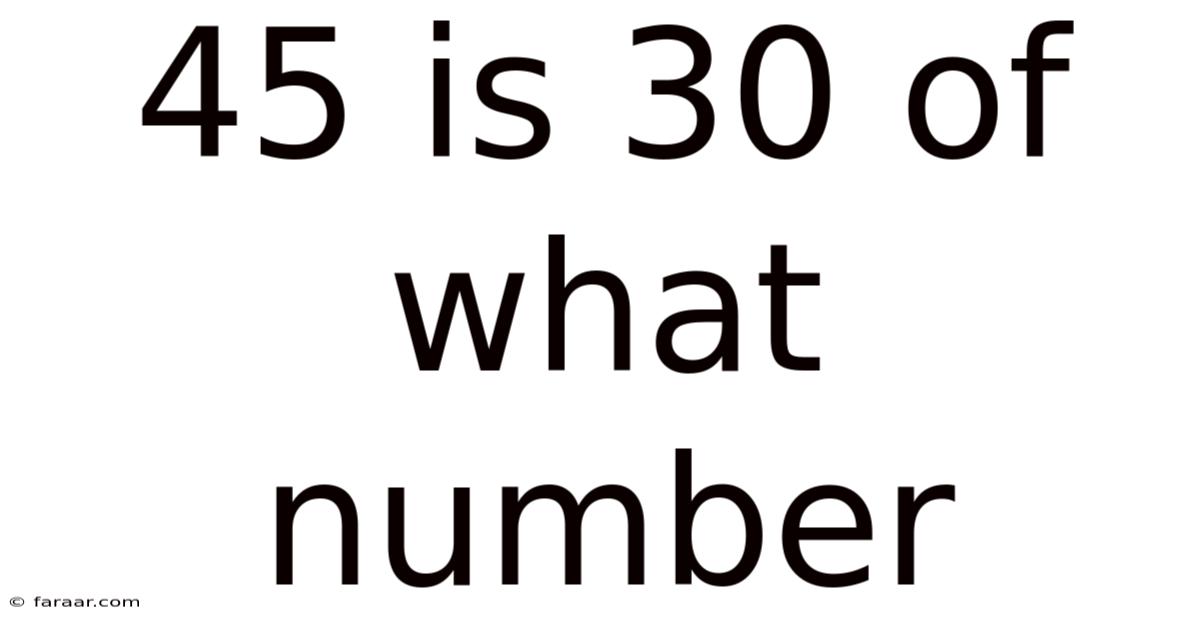
Table of Contents
45 is 30% of What Number? Unlocking the Power of Percentages
This article will delve into the seemingly simple question, "45 is 30% of what number?" While the answer might seem readily calculable, exploring the solution reveals a deeper understanding of percentages, their applications in everyday life, and the various methods used to solve such problems. We'll explore not just the immediate solution but also the underlying mathematical principles, providing you with the tools to confidently tackle similar percentage problems. This will equip you with practical skills applicable in various fields, from finance and business to everyday budgeting and problem-solving.
Understanding Percentages: A Foundation
Before diving into the solution, let's establish a firm grasp of what percentages represent. A percentage is simply a fraction expressed as a part of 100. The symbol "%" signifies "per hundred" or "out of 100". For example, 30% means 30 out of 100, which can also be expressed as the fraction 30/100 or the decimal 0.3. This fundamental understanding forms the bedrock of all percentage calculations.
Method 1: The Algebraic Approach
This is the most common and arguably the most elegant method for solving percentage problems. We can represent the problem algebraically using an equation. Let's say the unknown number is 'x'. The problem "45 is 30% of what number?" translates to the following equation:
45 = 0.3 * x
To solve for 'x', we need to isolate it. We can achieve this by dividing both sides of the equation by 0.3:
x = 45 / 0.3
Performing the division:
x = 150
Therefore, 45 is 30% of 150.
Method 2: The Proportion Method
The proportion method offers another powerful approach to solving percentage problems. It leverages the concept of equivalent ratios. We can set up a proportion as follows:
30/100 = 45/x
This equation states that the ratio of 30 to 100 (representing 30%) is equivalent to the ratio of 45 to the unknown number 'x'. To solve for 'x', we can cross-multiply:
30 * x = 45 * 100
30x = 4500
Now, divide both sides by 30:
x = 4500 / 30
x = 150
Again, we arrive at the solution: 45 is 30% of 150.
Method 3: The Percentage Formula
The percentage formula offers a more direct approach. The formula is:
Percentage = (Part / Whole) * 100
In our problem, we know the percentage (30%) and the part (45). We need to find the whole (x). Let's rearrange the formula to solve for the whole:
Whole = (Part / Percentage) * 100
Substituting the known values:
Whole = (45 / 30) * 100
Whole = 1.5 * 100
Whole = 150
Once more, the answer is 150.
Why Different Methods? Understanding the Underlying Principles
While all three methods lead to the same correct answer, understanding the different approaches allows for flexibility in solving a wider range of percentage problems. The algebraic method is generally preferred for its conciseness and efficiency. The proportion method highlights the relationship between ratios, offering a visual representation of the problem. The percentage formula provides a more direct approach, especially helpful when dealing with complex scenarios involving multiple percentages or variables. Choosing the most suitable method depends on personal preference and the specific context of the problem.
Practical Applications: Where Percentages Matter
Understanding percentage calculations is crucial in numerous real-life situations. Here are a few examples:
- Finance: Calculating interest rates, discounts, tax amounts, and investment returns all rely heavily on percentage calculations. For example, understanding how much a 30% discount reduces the original price of an item.
- Business: Analyzing sales figures, profit margins, market share, and growth rates all involve percentage calculations. A business might want to determine what percentage of its total sales comes from a specific product line.
- Everyday Life: Calculating tips in restaurants, understanding sale prices in stores, determining the percentage of a completed task, or calculating nutritional information all utilize percentage calculations. For example, calculating the percentage of daily calories consumed from carbohydrates.
- Science: Many scientific calculations, such as those involving concentrations of solutions or statistical analysis, use percentages.
- Data Analysis: Percentages are extensively used to represent proportions and trends within data sets.
Expanding Your Understanding: More Complex Percentage Problems
While the example problem "45 is 30% of what number?" is relatively straightforward, the principles we've discussed can be applied to more complex scenarios. For example:
- Finding the percentage increase or decrease: If a price increases from $100 to $130, what is the percentage increase? (Answer: 30%)
- Calculating multiple percentages: If a product is discounted by 20% and then by an additional 10%, what is the overall percentage discount? (Answer: 28%, not 30%)
- Solving problems involving unknown percentages: What percentage of 200 is 80? (Answer: 40%)
Mastering the fundamental concepts and approaches outlined in this article will provide you with the tools to tackle these and even more complex problems.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator for these problems?
A: Absolutely! Calculators can significantly simplify the calculations, particularly in more complex problems. However, understanding the underlying mathematical principles is crucial to choosing the correct operations and interpreting the results.
Q: What if the percentage is greater than 100%?
A: A percentage greater than 100% simply means that the "part" is larger than the "whole." This is common in contexts where growth or increase is involved. For instance, if a company's profits increase by 120%, it means the profits are now 220% of their original value.
Q: Are there any online tools or resources to help with percentage calculations?
A: Yes, numerous online calculators and resources are available to assist with percentage calculations. These tools can be helpful for verifying your answers or solving more complex problems. However, it's crucial to understand the underlying concepts to correctly use these tools and interpret their results.
Q: How can I improve my understanding of percentages further?
A: Practice is key. Try solving various percentage problems of increasing complexity. You can find practice problems in textbooks, online resources, or even create your own based on real-life scenarios. Focus on understanding the logic behind the different solution methods, and don't hesitate to seek clarification when needed.
Conclusion: Mastering Percentages for a Brighter Future
The ability to solve percentage problems is a valuable skill applicable across numerous aspects of life. Understanding the different methods – algebraic, proportion, and formula-based approaches – empowers you with flexibility and efficiency in tackling various percentage calculations. By mastering these methods and practicing regularly, you equip yourself not only with the ability to solve percentage problems accurately but also with a deeper understanding of the underlying mathematical concepts. This will undoubtedly prove beneficial in academic pursuits, professional endeavors, and navigating the intricacies of everyday life. So, embrace the power of percentages, and watch your problem-solving abilities soar!
Latest Posts
Latest Posts
-
How Many Hours Is 800 Miles
Sep 20, 2025
-
Gold Has A Density Of 19 3 G Cm3
Sep 20, 2025
-
General Formula To Describe The Variation
Sep 20, 2025
-
The Product Of A Number And 9
Sep 20, 2025
-
What Is The Molar Mass Of Ne
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 45 Is 30 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.