0 2 4 6 8 10
faraar
Sep 16, 2025 · 5 min read
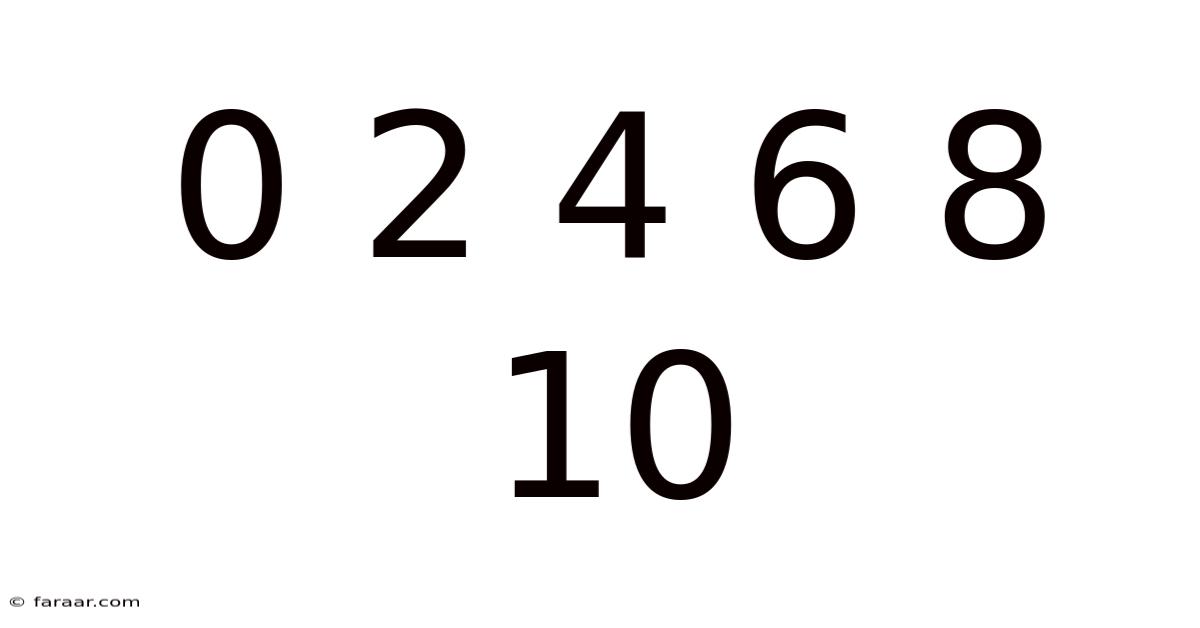
Table of Contents
Decoding the Sequence: Exploring the Pattern and Applications of 0, 2, 4, 6, 8, 10...
This article delves into the seemingly simple sequence of even numbers: 0, 2, 4, 6, 8, 10, and so on. While the pattern might appear basic at first glance, understanding its underlying structure unlocks a surprising range of mathematical concepts and practical applications across various fields. We'll explore the sequence's properties, its relationship to other mathematical concepts, and its relevance in everyday life and advanced studies. This exploration will cover its generation, applications in computer science, its connection to number theory, and address common questions about this fundamental sequence.
Understanding the Even Number Sequence
The sequence 0, 2, 4, 6, 8, 10... represents the set of even numbers. Even numbers are integers (whole numbers) that are perfectly divisible by 2, leaving no remainder. This fundamental property distinguishes them from odd numbers, which leave a remainder of 1 when divided by 2. The sequence's defining characteristic is its consistent increment of 2. This simple addition forms the basis of many mathematical operations and patterns.
Generating the Even Number Sequence
Generating this sequence is straightforward. We can express it using a simple arithmetic progression formula:
- a<sub>n</sub> = 2n
Where:
- a<sub>n</sub> represents the nth term in the sequence.
- n represents the position of the term (starting from n=0).
For example:
- a<sub>0</sub> = 2 * 0 = 0
- a<sub>1</sub> = 2 * 1 = 2
- a<sub>2</sub> = 2 * 2 = 4
- a<sub>3</sub> = 2 * 3 = 6
- and so on...
This formula provides a concise and efficient method for determining any term within the infinite sequence of even numbers.
Applications in Computer Science
The even number sequence, despite its simplicity, finds significant use in various aspects of computer science.
-
Iteration and Loops: Even numbers are frequently used to control loops in programming. For example, a program might process only even-indexed elements in an array or iterate through a loop with a step size of 2. This optimization technique can enhance program efficiency.
-
Bit Manipulation: At the lowest level, computers operate using binary code (0s and 1s). Even numbers are directly related to the concept of even numbers of bits. Understanding even and odd numbers of bits is crucial for tasks such as memory allocation, data structure design, and cryptographic operations.
-
Data Structures: Certain data structures, like linked lists or trees, might utilize even numbers for indexing or node identification, particularly in scenarios requiring optimized memory management or traversal algorithms.
-
Algorithms: Several algorithms leverage even numbers for their core logic. For instance, certain sorting algorithms or graph traversal algorithms might make use of even/odd distinctions to improve efficiency or handle specific problem constraints.
Connection to Number Theory
The sequence of even numbers is deeply intertwined with fundamental concepts in number theory.
-
Divisibility Rules: The divisibility rule for 2 is a direct consequence of the even number definition: A number is divisible by 2 if its last digit is an even number (0, 2, 4, 6, or 8).
-
Prime Numbers: Even numbers (excluding 2) are composite numbers, meaning they can be factored into smaller integers greater than 1. The study of prime numbers is closely related to even numbers as prime numbers are often defined as numbers not divisible by 2 (except for 2 itself).
-
Modular Arithmetic: Modular arithmetic involves performing arithmetic operations within a specific range (modulo). Even numbers play a significant role in understanding and applying modular arithmetic concepts, especially in cryptography and other fields that rely on number theory.
-
Perfect Numbers: A perfect number is a positive integer that is equal to the sum of its proper divisors (excluding itself). The study of perfect numbers reveals fascinating connections with even numbers. All known perfect numbers are even, although it remains an open question whether odd perfect numbers exist.
Even Numbers in Everyday Life
While the mathematical applications are important, even numbers also have practical relevance in our daily lives:
-
Counting: From counting pairs of shoes to organizing items in pairs, even numbers are implicitly used in our everyday routines.
-
Measurement: Many measurement systems use even numbers. For example, measurements in inches, centimeters, and other units often involve even number increments.
-
Calendars: The number of days in certain months are even, influencing scheduling and planning activities.
-
Games and Puzzles: Many games and puzzles utilize even numbers in their design and rules, often relating to turns, scoring systems, or strategic decision-making.
Frequently Asked Questions (FAQs)
Q1: Is zero an even number?
A1: Yes, zero is an even number because it's divisible by 2 with a remainder of 0.
Q2: What is the difference between even and odd numbers?
A2: Even numbers are integers divisible by 2 without any remainder, while odd numbers leave a remainder of 1 when divided by 2.
Q3: Are all even numbers divisible by 4?
A3: No, only even numbers that are multiples of 4 (such as 4, 8, 12, etc.) are divisible by 4.
Q4: How can I determine if a large number is even or odd?
A4: You only need to check its last digit. If the last digit is 0, 2, 4, 6, or 8, the number is even; otherwise, it's odd.
Q5: What is the significance of the even number sequence in advanced mathematics?
A5: The even number sequence serves as a foundation for many more advanced mathematical concepts, impacting fields like number theory, abstract algebra, and analysis. Its properties and relationships with other number sets provide insights into the structure of numbers and mathematical systems.
Conclusion
The sequence 0, 2, 4, 6, 8, 10... might seem simple, but its significance extends far beyond its apparent simplicity. From its fundamental role in arithmetic progressions to its practical applications in computer science and its deep connections to number theory, the sequence of even numbers reveals a rich tapestry of mathematical concepts and real-world relevance. Understanding this sequence is not just about recognizing a pattern; it’s about appreciating the foundational building blocks that underpin more complex mathematical structures and applications across various fields of study and daily life. Its seemingly simple nature belies a profound influence on our understanding of numbers and their utility in the world around us. Further exploration into its properties and applications will continue to reveal new and insightful connections within the broader landscape of mathematics.
Latest Posts
Latest Posts
-
How Did The Colonist React To The Sugar Act
Sep 17, 2025
-
How Do You Find The Sides Of A Polygon
Sep 17, 2025
-
Best Breakfast For A Test Day
Sep 17, 2025
-
How Many Grams Is 200 Ml
Sep 17, 2025
-
What Is The Product Of 3x X2 4
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 0 2 4 6 8 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.