What Is The Product Of 3x X2 4
faraar
Sep 17, 2025 · 5 min read
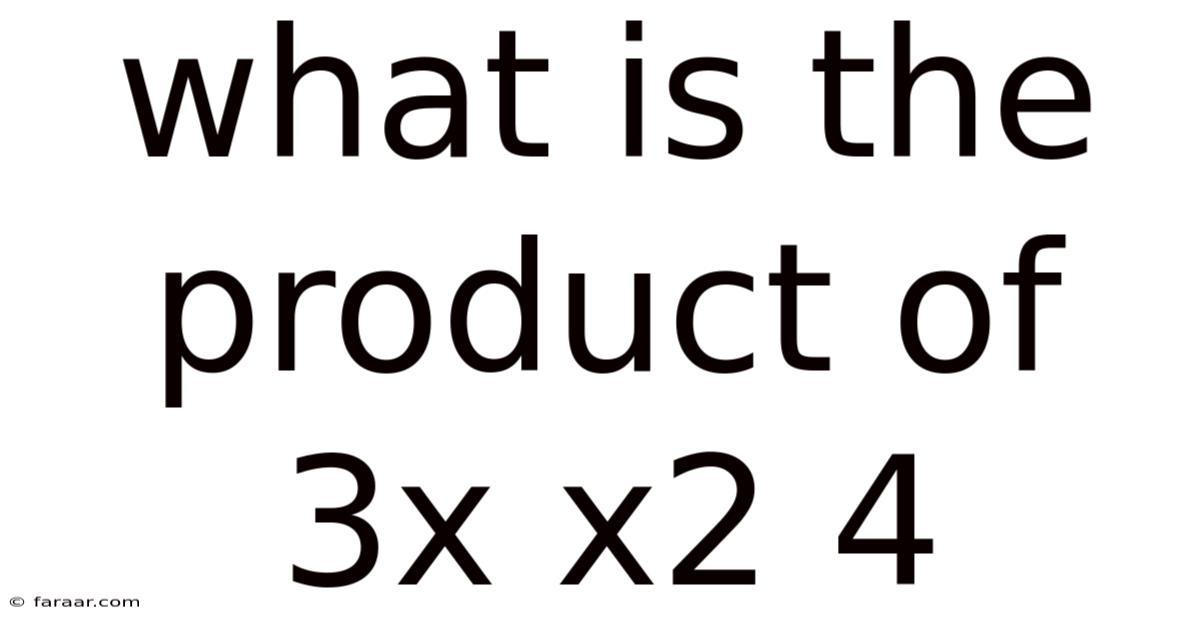
Table of Contents
Decoding the Expression: What is the Product of 3x, x², and 4?
Understanding algebraic expressions is fundamental to success in mathematics and related fields. This article will thoroughly explore the seemingly simple question: "What is the product of 3x, x², and 4?" We'll break down the problem step-by-step, providing a clear explanation suitable for all levels, from beginners to those looking to refresh their algebraic skills. We'll cover the core concepts, delve into the process of simplification, and address frequently asked questions. This comprehensive guide aims to not only solve the problem but also enhance your overall understanding of algebraic manipulation and the properties of exponents.
Understanding the Terms
Before tackling the multiplication, let's clarify the individual components of the expression:
-
3x: This term represents the product of 3 and x. The 'x' is a variable, representing an unknown value. The '3' is a coefficient, a numerical factor multiplying the variable.
-
x²: This term represents x multiplied by itself (x * x). The '2' is an exponent, indicating the number of times the base (x) is multiplied by itself. This is also known as 'x squared'.
-
4: This is a constant, a numerical value that doesn't change.
The Multiplication Process: Step-by-Step
To find the product of 3x, x², and 4, we simply multiply these terms together. We can rearrange the terms for easier calculation, utilizing the commutative property of multiplication, which states that the order of factors doesn't affect the product (a x b = b x a).
-
Rearrange the terms: Let's group the numerical coefficients and the variables together: (3 x 4) x (x x x²)
-
Multiply the coefficients: 3 multiplied by 4 equals 12.
-
Multiply the variables: This involves understanding the rules of exponents. When multiplying variables with the same base (in this case, 'x'), we add their exponents. Therefore, x multiplied by x² is x¹⁺² = x³.
-
Combine the results: Combining the results from steps 2 and 3, we get the final answer: 12x³.
Therefore, the product of 3x, x², and 4 is 12x³.
Expanding the Understanding: Properties of Exponents
The multiplication of variables with exponents is a crucial aspect of algebra. Let's delve deeper into the underlying principle:
- Product of Powers Property: When multiplying two exponential terms with the same base, you add their exponents: xᵃ * xᵇ = x⁽ᵃ⁺ᵇ⁾.
This property is fundamental to simplifying algebraic expressions. In our example, x¹ * x² = x⁽¹⁺²⁾ = x³. Understanding this property allows you to efficiently simplify more complex algebraic expressions involving variables raised to various powers.
-
Power of a Power Property: When raising an exponential term to a power, you multiply the exponents: (xᵃ)ᵇ = x⁽ᵃᵇ⁾. For example, (x²)³ = x⁽²³⁾ = x⁶.
-
Power of a Product Property: When raising a product to a power, you raise each factor to that power: (ab)ⁿ = aⁿbⁿ. For instance, (2x)³ = 2³x³ = 8x³.
Illustrative Examples: Expanding the Concept
Let's consider a few more examples to solidify your understanding:
-
Example 1: Find the product of 2y, y³, and 5. (2y)(y³)(5) = (2 x 5)(y x y³) = 10y⁴
-
Example 2: Find the product of -3a², 4a, and 2a⁴. (-3a²)(4a)(2a⁴) = (-3 x 4 x 2)(a² x a x a⁴) = -24a⁷
-
Example 3: Find the product of ½x³, 6x², and 4x. (½x³)(6x²)(4x) = (½ x 6 x 4)(x³ x x² x x) = 12x⁶
These examples illustrate the consistent application of the rules of exponents and the commutative property of multiplication in simplifying algebraic expressions.
Addressing Frequently Asked Questions (FAQ)
Q1: What if the expression contains different variables?
A1: If the expression involves different variables (e.g., 2x, 3y, and 4z), you can still multiply the coefficients, but you cannot combine the variables through exponent addition. The result would be a product of the variables: 24xyz.
Q2: What happens if there are negative coefficients?
A2: Negative coefficients are treated like any other number during multiplication. Remember the rules of multiplying signed numbers: a positive multiplied by a positive is positive; a negative multiplied by a positive is negative; and a negative multiplied by a negative is positive.
Q3: Can I simplify the expression further after finding the product?
A3: In this specific case (12x³), there's no further simplification possible unless a value is assigned to 'x'. However, in more complex expressions, you might be able to factor or further simplify the result.
Q4: Why is understanding this concept important?
A4: Mastering algebraic manipulation, including the multiplication of terms with exponents, is crucial for solving equations, simplifying complex formulas, and progressing to more advanced mathematical concepts in algebra, calculus, and beyond. It forms the backbone of numerous scientific and engineering calculations.
Conclusion: Mastering Algebraic Manipulation
This article provided a detailed explanation of how to find the product of 3x, x², and 4. We not only solved the problem (resulting in 12x³) but also delved into the fundamental principles underlying algebraic manipulation, including the properties of exponents and the commutative property of multiplication. By understanding these principles and practicing various examples, you'll build a strong foundation in algebra, setting you up for success in more complex mathematical endeavors. Remember, consistent practice is key to mastering these concepts. Work through additional problems and challenge yourself to tackle increasingly complex expressions. With dedication and practice, you'll become proficient in manipulating algebraic expressions and confidently solving a wide range of mathematical problems.
Latest Posts
Latest Posts
-
Express As A Product Of Linear Factors
Sep 17, 2025
-
What Is The Relationship Between Concentration And Absorbance
Sep 17, 2025
-
A Comparison Of Two Unlike Things Using Like Or As
Sep 17, 2025
-
Domains And Ranges From Word Problems
Sep 17, 2025
-
Do You Have To Straighten Hair Before Curling
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is The Product Of 3x X2 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.