Z Varies Jointly As X And Y
faraar
Sep 14, 2025 · 6 min read
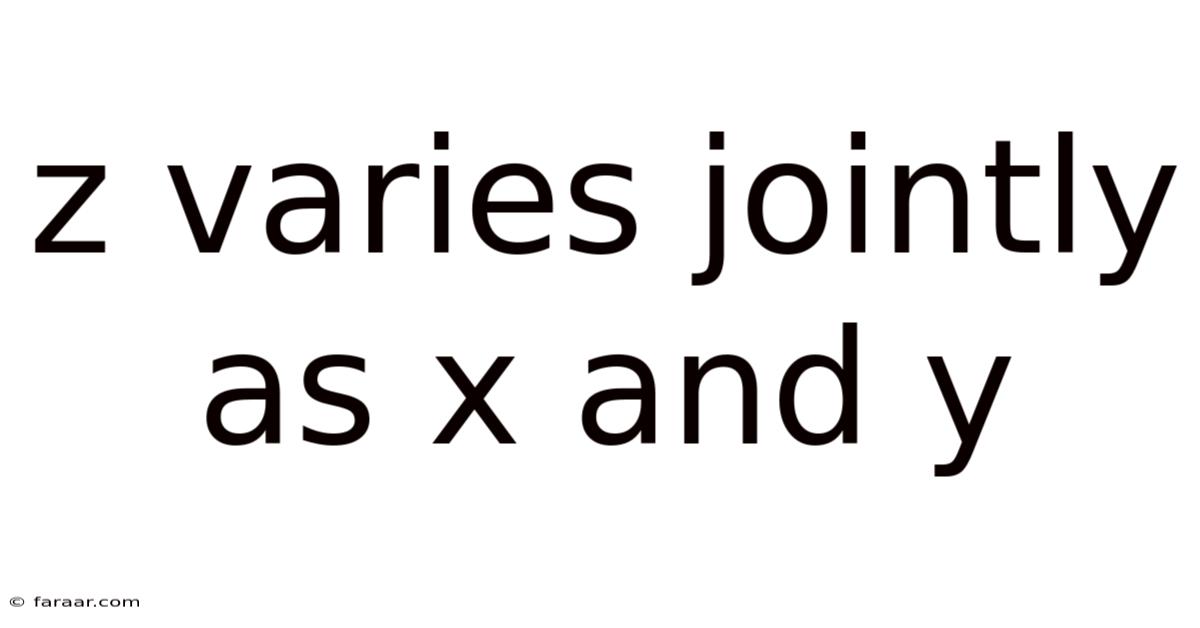
Table of Contents
Understanding Joint Variation: When Z Varies Jointly as X and Y
Joint variation is a fundamental concept in algebra that describes the relationship between three or more variables where one variable depends on the product of two or more other variables. This article delves deep into the concept of "z varies jointly as x and y," exploring its mathematical representation, practical applications, and problem-solving techniques. We will unravel the intricacies of this concept, providing clear explanations and examples to solidify your understanding. Understanding joint variation is crucial for various fields, from physics and engineering to economics and statistics.
Introduction to Joint Variation
In simple terms, when we say "z varies jointly as x and y," it means that z is directly proportional to both x and y. This implies that if x increases, z increases proportionally, and if y increases, z increases proportionally as well. Conversely, if either x or y decreases, z decreases proportionally. The relationship can be expressed mathematically using a constant of proportionality, often denoted by 'k'.
The general equation representing joint variation is:
z = kxy
where:
- z is the dependent variable.
- x and y are the independent variables.
- k is the constant of proportionality. This constant represents the rate at which z changes in response to changes in x and y.
This equation forms the bedrock of understanding and solving problems related to joint variation. The value of 'k' remains constant throughout a specific problem, reflecting the inherent relationship between the variables.
Understanding the Constant of Proportionality (k)
The constant of proportionality, 'k', is a crucial element in the equation. It represents the factor by which the joint variation occurs. Its value is determined by the specific relationship between the variables in a given context. To find 'k', we need a set of values for z, x, and y. Once we find 'k', we can use the equation to predict the value of z for any given values of x and y.
For example, if we know that when x = 2 and y = 3, z = 12, we can solve for k:
12 = k * 2 * 3
12 = 6k
k = 12/6 = 2
Therefore, the equation for this specific joint variation is:
z = 2xy
This equation now allows us to calculate z for any combination of x and y values within the given context.
Solving Problems Involving Joint Variation
Solving problems involving joint variation typically involves two main steps:
-
Finding the constant of proportionality (k): This requires a set of known values for z, x, and y. Substitute these values into the equation z = kxy and solve for k.
-
Using the equation to find unknown values: Once k is known, you can use the equation z = kxy to solve for any unknown value (z, x, or y) given the other two.
Let's illustrate this with a few examples:
Example 1:
The volume (V) of a rectangular prism varies jointly as its length (l), width (w), and height (h). If V = 60 cubic cm when l = 5 cm, w = 3 cm, and h = 4 cm, find the volume when l = 6 cm, w = 4 cm, and h = 5 cm.
- Step 1: Find k
60 = k * 5 * 3 * 4
60 = 60k
k = 1
- Step 2: Use k to find the new volume
V = 1 * 6 * 4 * 5
V = 120 cubic cm
Therefore, the volume of the rectangular prism is 120 cubic cm when l = 6 cm, w = 4 cm, and h = 5 cm.
Example 2:
The cost (C) of building a house varies jointly as the number of square feet (S) and the cost per square foot (c). If it costs $150,000 to build a 2,500 square foot house with a cost per square foot of $60, what would be the cost of building a 3,000 square foot house with the same cost per square foot?
- Step 1: Find k
150000 = k * 2500 * 60
150000 = 150000k
k = 1
- Step 2: Use k to find the new cost
C = 1 * 3000 * 60
C = $180,000
Therefore, the cost of building a 3,000 square foot house would be $180,000.
Beyond the Basics: Variations on Joint Variation
While the basic form, z = kxy, is fundamental, joint variation can involve more than two independent variables. For instance, "z varies jointly as x, y, and w" would be represented as:
z = kxwy
The process of solving problems remains the same; find k using a known set of values and then use the equation to solve for unknowns.
Inverse Variation Combined with Joint Variation
It's also possible to have a combination of joint and inverse variation. For example, "z varies jointly as x and y and inversely as w" would be represented as:
z = kxy/w
In this case, z increases proportionally with x and y but decreases proportionally with w. Solving problems involving such combined variations requires careful attention to the relationship between all the variables.
Real-World Applications of Joint Variation
Joint variation finds applications in numerous real-world scenarios:
- Physics: Calculating the force of gravity, calculating the volume of a cylinder or sphere, understanding the relationship between electrical resistance, current, and voltage (Ohm's Law).
- Engineering: Designing structures, calculating the stress on a material, determining the capacity of a container.
- Economics: Modeling the relationship between supply, demand, and price.
- Chemistry: Understanding the ideal gas law, which relates pressure, volume, temperature, and the number of moles of a gas.
Frequently Asked Questions (FAQ)
Q: What is the difference between direct variation and joint variation?
A: Direct variation involves only two variables where one is directly proportional to the other (z = kx). Joint variation involves three or more variables where one variable is directly proportional to the product of two or more others (z = kxy, z = kxwy, etc.).
Q: Can k ever be zero?
A: No. If k were zero, it would imply that z is always zero, regardless of the values of x and y, making it a trivial relationship.
Q: What if the relationship is not directly proportional but instead inversely proportional to one or more variables?
A: That would represent a combination of joint and inverse variation, as described earlier. The equation would then include the independent variables in the denominator.
Q: How do I handle negative values for x, y, or z?
A: Negative values are handled just as positive values. The equation z = kxy remains valid; the sign of z will depend on the signs of k, x, and y according to the rules of multiplication.
Conclusion
Understanding joint variation is crucial for anyone working with multiple interacting variables. By mastering the core concepts and problem-solving techniques, you can effectively analyze and predict the behavior of systems governed by joint variation relationships. Remember that the constant of proportionality, k, is the key to unlocking these relationships. This concept forms a solid foundation for more advanced mathematical and scientific studies, paving the way to a deeper comprehension of the interconnectedness of various phenomena in the world around us. The ability to recognize and model joint variation enhances problem-solving capabilities across diverse fields and empowers you to make accurate predictions based on the relationships between multiple variables.
Latest Posts
Latest Posts
-
Average Velocity Between Two Time Intervals
Sep 14, 2025
-
How To Find End Behavior Of A Graph
Sep 14, 2025
-
What Is A Real Solution In Math
Sep 14, 2025
-
Why Does The Green Knight Forgive Gawain
Sep 14, 2025
-
How Do You Calculate The Mass In Grams
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Z Varies Jointly As X And Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.