Y 5x 6 Solve For X
faraar
Sep 07, 2025 · 6 min read
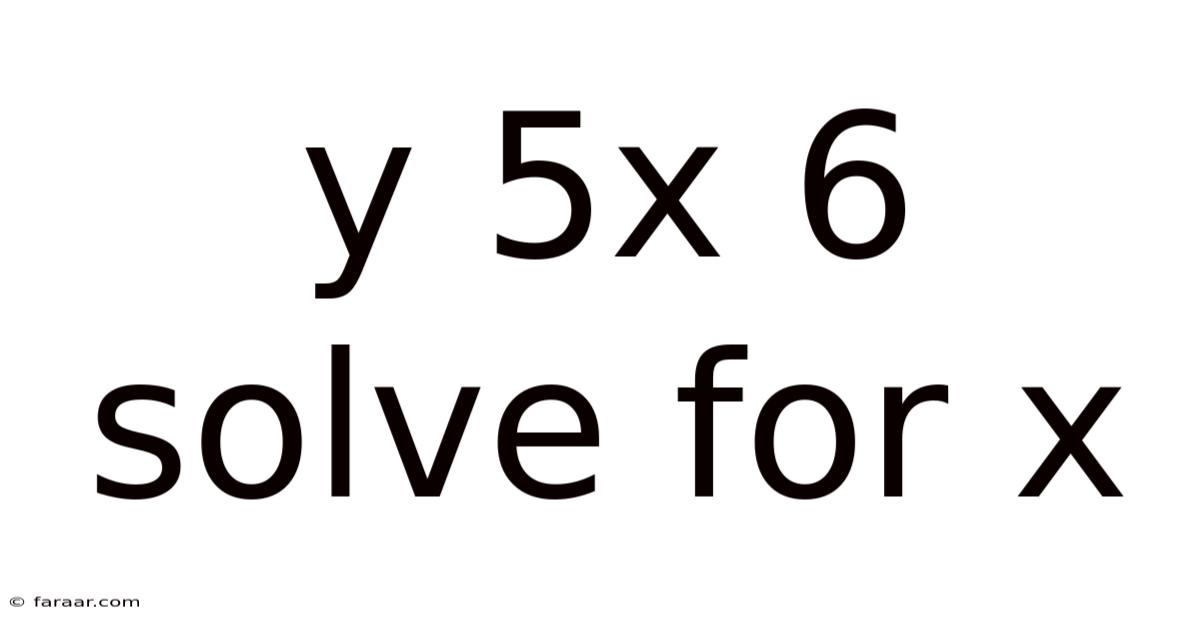
Table of Contents
Solving for x: A Deep Dive into the Equation y = 5x + 6
This article provides a comprehensive guide on how to solve for x in the linear equation y = 5x + 6. We will explore various methods, delve into the underlying mathematical principles, and address common questions and potential challenges. Understanding this seemingly simple equation is crucial for mastering fundamental algebraic concepts and building a strong foundation for more advanced mathematics. We'll cover everything from basic algebraic manipulation to the graphical representation of the solution, ensuring a complete and insightful understanding.
Introduction: Understanding Linear Equations
Before jumping into the solution, let's establish a clear understanding of what we're dealing with. The equation y = 5x + 6 is a linear equation. This means that when graphed, it represents a straight line. Linear equations are characterized by their simplicity and the consistent relationship between the variables x and y. In this equation:
- y represents the dependent variable. Its value depends on the value of x.
- x represents the independent variable. We can choose any value for x, and the equation will give us the corresponding value of y.
- 5 is the slope of the line. It indicates the rate at which y changes with respect to x. A slope of 5 means that for every one-unit increase in x, y increases by 5 units.
- 6 is the y-intercept. It's the value of y when x is equal to 0. The line intersects the y-axis at the point (0, 6).
Our goal is to solve for x, meaning we want to isolate x on one side of the equation, expressing it in terms of y.
Method 1: Algebraic Manipulation
This is the most common and straightforward method. We'll use basic algebraic principles to isolate x.
-
Subtract 6 from both sides: The goal is to move the constant term (6) to the other side of the equation. Subtracting 6 from both sides maintains the balance of the equation:
y - 6 = 5x + 6 - 6
This simplifies to:
y - 6 = 5x
-
Divide both sides by 5: Now we need to isolate x by dividing both sides of the equation by its coefficient (5):
(y - 6) / 5 = 5x / 5
This simplifies to:
x = (y - 6) / 5
This is our solution. For any given value of y, we can substitute it into this equation to find the corresponding value of x.
Method 2: Using the Formula for Solving Linear Equations
While the above method is intuitive, we can also use a more general formula for solving linear equations of the form ax + b = c. In our case, a = 5, b = -6, and c = y. The general formula is:
x = (c - b) / a
Substituting our values, we get:
x = (y - (-6)) / 5
x = (y + 6) / 5
Notice that this is equivalent to the solution we obtained through algebraic manipulation. This formula provides a more structured approach, particularly useful for solving a large number of similar equations.
Graphical Representation
The equation y = 5x + 6 can be graphically represented as a straight line. The y-intercept is 6, meaning the line crosses the y-axis at the point (0, 6). The slope is 5, indicating a steep positive incline. To find x for a specific y value graphically, you would locate the point on the y-axis corresponding to that y value, then trace a horizontal line to the point where it intersects the line representing y = 5x + 6. From that intersection point, draw a vertical line down to the x-axis to find the corresponding x value. This visual representation helps to solidify the understanding of the relationship between x and y.
Explanation of the Mathematical Principles
The methods used above rely on fundamental algebraic principles:
- The Addition Property of Equality: Adding or subtracting the same value from both sides of an equation does not change its equality.
- The Multiplication Property of Equality: Multiplying or dividing both sides of an equation by the same non-zero value does not change its equality.
These properties are essential for manipulating equations and isolating specific variables. Understanding these principles allows for flexibility in solving various algebraic problems.
Illustrative Examples
Let's illustrate the solution with some examples:
-
Example 1: If y = 11, what is x?
Using the formula x = (y - 6) / 5, we substitute y = 11:
x = (11 - 6) / 5 = 5 / 5 = 1
Therefore, when y = 11, x = 1.
-
Example 2: If y = -4, what is x?
Substituting y = -4 into the formula:
x = (-4 - 6) / 5 = -10 / 5 = -2
Therefore, when y = -4, x = -2.
-
Example 3: If y = 0, what is x?
Substituting y = 0:
x = (0 - 6) / 5 = -6/5 = -1.2
Therefore, when y = 0, x = -1.2
Frequently Asked Questions (FAQ)
-
Q: What if the equation is different? For example, y = 2x + 10?
A: The same principles apply. You would follow the same steps: subtract the constant term from both sides and then divide by the coefficient of x. The solution for y = 2x + 10 would be x = (y - 10) / 2.
-
Q: Can I solve for y instead of x?
A: Yes, the equation is already solved for y. You can easily find the value of y for any given value of x by simply substituting the x value into the equation y = 5x + 6.
-
Q: What if the equation has more than two variables?
A: Solving equations with more than two variables requires more advanced techniques, often involving systems of equations and matrix operations. This is beyond the scope of this introductory explanation.
-
Q: Why is the slope important?
A: The slope represents the rate of change. In this case, a slope of 5 signifies that for each unit increase in x, y increases by 5 units. This is crucial for understanding the behavior and characteristics of the linear relationship.
Conclusion: Mastering the Fundamentals
Solving for x in the equation y = 5x + 6 is a fundamental skill in algebra. By understanding the underlying principles of algebraic manipulation and applying the steps outlined above, you can confidently solve this and similar linear equations. Remember, mastering these basic concepts forms the bedrock for tackling more complex mathematical problems in the future. Practice is key – the more you work with these types of equations, the more comfortable and proficient you'll become. Don't hesitate to work through more examples and test your understanding by solving similar equations with different coefficients and constants. This iterative process is crucial for solidifying your grasp of these fundamental algebraic concepts.
Latest Posts
Latest Posts
-
How To Factor Trinomials A Is Greater Than 1
Sep 08, 2025
-
Reading And Writing Tutors Near Me
Sep 08, 2025
-
Feet Per Second At 70 Mph
Sep 08, 2025
-
A Quadrilateral Pqrs Is Inscribed In A Circle
Sep 08, 2025
-
Words That Start With G In French
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about Y 5x 6 Solve For X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.