Y 2x 1 2x Y 3
faraar
Sep 12, 2025 · 6 min read
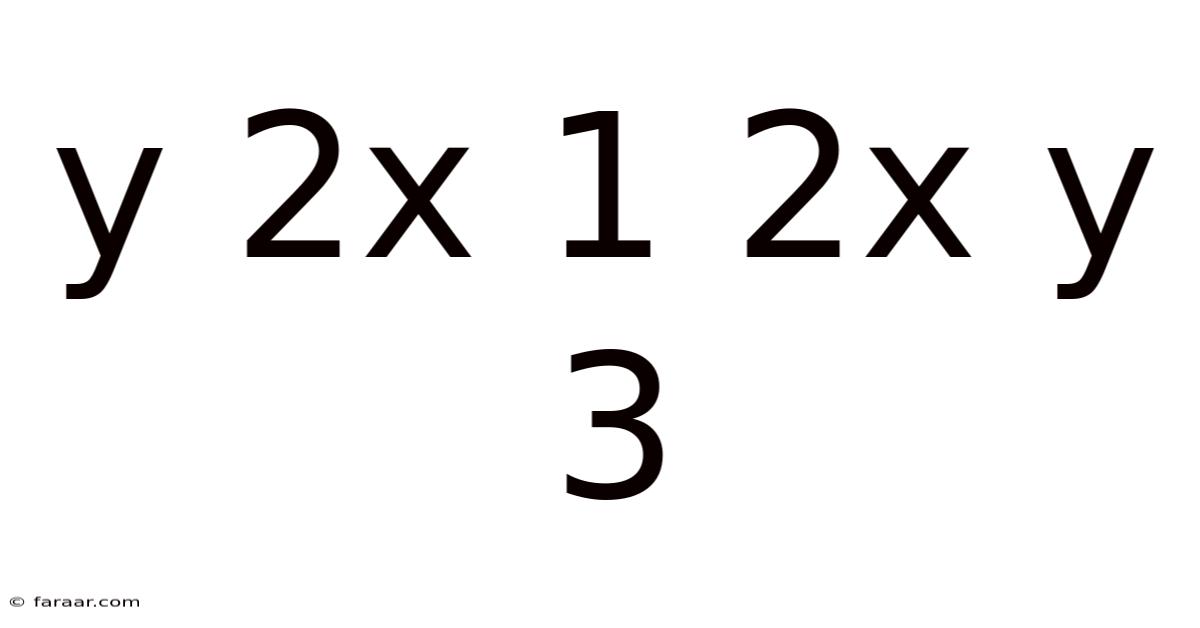
Table of Contents
Exploring the Mathematical Relationship: y = 2x + 1 and 2x + y = 3
This article delves into the mathematical relationship between two linear equations: y = 2x + 1 and 2x + y = 3. We will explore their graphical representations, solve for their intersection point (if any), and discuss the broader implications of understanding systems of linear equations. Understanding these concepts is fundamental to various fields, including physics, engineering, economics, and computer science. We'll break down the concepts in a clear and accessible manner, perfect for students and anyone looking to refresh their algebra skills.
Introduction to Linear Equations
A linear equation represents a straight line on a graph. It's characterized by its constant rate of change, meaning the relationship between the variables remains consistent. The general form of a linear equation is often written as:
- y = mx + c
where:
- 'y' and 'x' are variables.
- 'm' represents the slope (gradient) of the line, indicating its steepness.
- 'c' represents the y-intercept, the point where the line crosses the y-axis (when x = 0).
Our focus lies on two specific linear equations:
-
y = 2x + 1: This equation is already in the slope-intercept form (y = mx + c), making it easy to identify the slope (m = 2) and the y-intercept (c = 1).
-
2x + y = 3: This equation is in the standard form (Ax + By = C). To easily visualize it and compare it with the first equation, we'll convert it into the slope-intercept form by solving for y:
Subtract 2x from both sides: y = -2x + 3
Now we can clearly see the slope (m = -2) and the y-intercept (c = 3).
Graphical Representation
Let's visualize these equations graphically. We can plot these lines on a Cartesian coordinate system (x-y plane). To do this effectively, we'll find at least two points for each line and connect them to form the straight lines.
For y = 2x + 1:
- If x = 0, then y = 2(0) + 1 = 1. So, one point is (0, 1).
- If x = 1, then y = 2(1) + 1 = 3. Another point is (1, 3).
For y = -2x + 3:
- If x = 0, then y = -2(0) + 3 = 3. So, one point is (0, 3).
- If x = 1, then y = -2(1) + 3 = 1. Another point is (1, 1).
By plotting these points and drawing lines through them, we can observe that the two lines intersect at a single point. This intersection point represents the solution that satisfies both equations simultaneously.
Solving the System of Equations
There are several methods to solve a system of linear equations. Here, we'll use two common methods: substitution and elimination.
1. Substitution Method:
Since we have y expressed in terms of x in the first equation (y = 2x + 1), we can substitute this expression for 'y' into the second equation:
2x + (2x + 1) = 3
Now, solve for x:
4x + 1 = 3 4x = 2 x = 1/2 or 0.5
Now, substitute the value of x back into either of the original equations to find y. Let's use the first equation:
y = 2(1/2) + 1 = 2
Therefore, the solution to the system of equations is x = 0.5 and y = 2. The point of intersection is (0.5, 2).
2. Elimination Method:
This method involves adding or subtracting the equations to eliminate one variable. Notice that if we add the two equations together, the 'x' terms will cancel out:
(y = 2x + 1)
- (y = -2x + 3)
2y = 4
Solving for y: y = 2
Now substitute this value of y into either equation to solve for x. Using the first equation:
2 = 2x + 1 1 = 2x x = 1/2
Again, we find the solution x = 0.5 and y = 2.
Mathematical Significance and Applications
Solving systems of linear equations is crucial for many mathematical and real-world applications. Here are some examples:
-
Break-Even Analysis: In business, determining the point where revenue equals cost (the break-even point) often involves solving a system of linear equations. One equation represents revenue, and the other represents cost.
-
Supply and Demand: Economists use linear equations to model supply and demand curves. The intersection point of these curves represents the market equilibrium price and quantity.
-
Physics and Engineering: Linear equations are used extensively in physics and engineering to model relationships between variables, such as force, velocity, and displacement.
-
Computer Graphics and Game Development: Linear equations are fundamental to computer graphics and game development for tasks like 2D and 3D transformations, collision detection, and ray tracing.
-
Network Analysis: In network analysis, linear equations help determine the flow of resources or information through a network.
Further Exploration: Systems of Equations with Multiple Solutions or No Solutions
While the system we examined has a unique solution (one point of intersection), it's important to note that systems of linear equations can have:
-
Infinitely Many Solutions: This occurs when the two equations represent the same line (they are linearly dependent). Any point on the line satisfies both equations.
-
No Solution: This happens when the lines are parallel (they have the same slope but different y-intercepts). They never intersect, indicating no common solution.
Frequently Asked Questions (FAQ)
Q: What if I get a different solution using a different method?
A: If you obtain a different solution using a different method, double-check your calculations in each step. There might be an arithmetic error somewhere. Linear equation solutions should be consistent regardless of the method used.
Q: Can I solve these equations using graphical methods alone?
A: Yes, you can approximate the solution graphically by carefully plotting the lines and visually identifying the intersection point. However, this method may not be as accurate as algebraic methods, especially if the intersection point involves fractions or decimals.
Q: What is the significance of the slope in these equations?
A: The slope represents the rate of change of y with respect to x. In our example, the first equation (y = 2x + 1) has a positive slope (2), indicating that y increases as x increases. The second equation (y = -2x + 3) has a negative slope (-2), indicating that y decreases as x increases. The slopes also tell us about the relationship between the lines (in this case they are not parallel, hence, they intersect).
Q: Are there more advanced methods to solve systems of equations?
A: Yes, for systems involving more than two equations or non-linear equations, more advanced techniques like matrix methods (Gaussian elimination, Cramer's rule), iterative methods, or numerical analysis techniques might be required.
Conclusion
Understanding the relationship between linear equations, such as y = 2x + 1 and 2x + y = 3, provides a foundation for tackling more complex mathematical problems. By mastering techniques like substitution and elimination, and understanding the graphical representation of these equations, we can confidently solve systems of linear equations and apply these skills to various practical scenarios across different disciplines. Remember, consistent practice and a solid grasp of fundamental algebraic concepts are key to success in this area. Keep exploring, keep practicing, and you'll find yourself becoming increasingly proficient in solving these types of problems.
Latest Posts
Latest Posts
-
What Is Less Than 1 2 Inch
Sep 12, 2025
-
How To Find Upper And Lower Limits In Statistics
Sep 12, 2025
-
Express Each Relation As A Table Graph And Mapping
Sep 12, 2025
-
1 2 3 Cup Equals How Many Ounces
Sep 12, 2025
-
Write The Equation Of The Conic Section Shown Below
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Y 2x 1 2x Y 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.