X Squared Divided By X Squared
faraar
Aug 26, 2025 · 5 min read
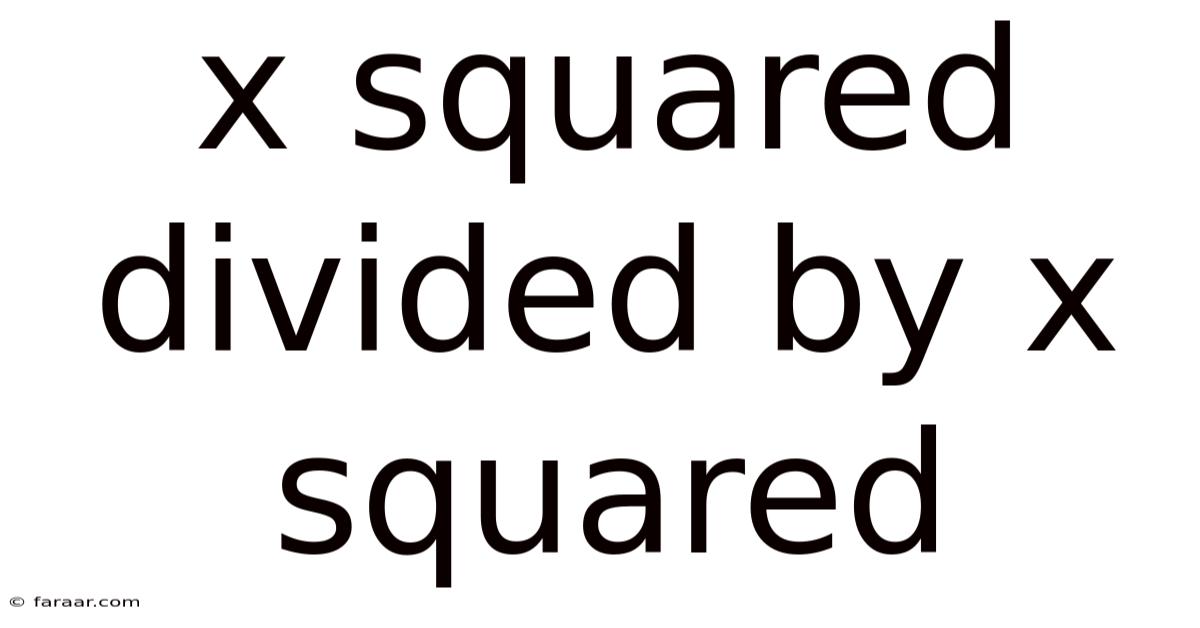
Table of Contents
Understanding x² ÷ x²: A Deep Dive into Mathematical Simplification
Many students encounter the expression x² ÷ x² and wonder about its simplification. This seemingly simple division problem opens the door to understanding fundamental algebraic concepts like exponents, division rules, and the concept of undefined values. This article will provide a comprehensive explanation, exploring various scenarios and addressing common misconceptions, ensuring a thorough understanding of this mathematical operation.
Introduction: The Basics of Exponents and Division
Before diving into x² ÷ x², let's refresh our understanding of exponents and division. An exponent (or power) indicates how many times a base number is multiplied by itself. In x², 'x' is the base, and '2' is the exponent, meaning x multiplied by itself (x * x). Division, on the other hand, is the process of splitting a quantity into equal parts.
When dealing with algebraic expressions involving exponents, we utilize several key rules:
-
The Quotient Rule of Exponents: When dividing two terms with the same base, we subtract the exponents. For example, x⁵ ÷ x² = x⁽⁵⁻²⁾ = x³. This rule is central to simplifying x² ÷ x².
-
The Power of a Quotient Rule: This rule states that (a/b)ⁿ = aⁿ/bⁿ. While not directly used in simplifying x² ÷ x², it becomes relevant when considering more complex expressions.
-
Zero Exponent Rule: Any non-zero number raised to the power of zero is equal to 1. This rule, x⁰ = 1 (where x ≠ 0), will be important when we consider the implications of our simplification.
Step-by-Step Simplification of x² ÷ x²
Applying the quotient rule of exponents directly to x² ÷ x², we have:
x² ÷ x² = x⁽²⁻²⁾ = x⁰
Now, applying the zero exponent rule, we get:
x⁰ = 1 (provided x ≠ 0)
Therefore, the simplified form of x² ÷ x² is 1, as long as x is not equal to zero.
Why is x ≠ 0 Crucial?
The condition x ≠ 0 is critical because division by zero is undefined in mathematics. Let's explore why:
Division can be interpreted as the inverse operation of multiplication. If we have a ÷ b = c, then it implies that b * c = a. Let's apply this to the case of x² ÷ x²:
If x² ÷ x² = 1, then it must be true that x² * 1 = x². This holds true for any value of x except zero.
However, if we were to attempt to divide by zero:
x² ÷ 0 = ? There is no number that, when multiplied by 0, will result in x². This is why division by zero is undefined. It breaks the fundamental rules of arithmetic.
To illustrate further, consider the following:
Let's say x = 2. Then x² ÷ x² = 4 ÷ 4 = 1.
Let's say x = 10. Then x² ÷ x² = 100 ÷ 100 = 1.
Let's say x = 0.1. Then x² ÷ x² = 0.01 ÷ 0.01 = 1.
Notice a pattern? Regardless of the non-zero value of x, the result is always 1. However, if x=0, we encounter the undefined operation 0 ÷ 0, which has no meaningful mathematical solution.
Exploring the Concept Graphically
Visualizing the function y = x²/x² can further solidify our understanding. If we plot this function, we'll see a horizontal line at y = 1, except at x = 0, where there's a hole or discontinuity in the graph. This hole represents the undefined point where x = 0. The graph visually demonstrates that for all non-zero values of x, the expression simplifies to 1.
Addressing Common Misconceptions
Several misconceptions often arise when simplifying expressions like x² ÷ x². Let's clarify them:
-
Incorrect Cancellation: Some students might incorrectly cancel x² with x², leading to an answer of 0. This is wrong because cancelling implies subtracting the exponents, not eliminating the entire term.
-
Ignoring the x ≠ 0 Condition: It's essential to always remember the crucial condition that x cannot be zero. Failing to mention this limitation makes the solution incomplete and potentially misleading.
-
Confusing with other Operations: It is important to understand that x² ÷ x² is not the same as x² - x². The former is division, while the latter is subtraction. Their results will be vastly different.
Beyond the Basics: Extending the Concept
The principle demonstrated by x² ÷ x² extends to more complex expressions involving higher powers and multiple variables. For instance:
-
x⁵y³ ÷ x³y² = x⁽⁵⁻³⁾y⁽³⁻²⁾ = x²y (assuming x and y are not zero)
-
(x⁴z²) / (x²z) = x⁽⁴⁻²⁾z⁽²⁻¹⁾ = x²z (assuming x and z are not zero)
These examples highlight the consistent application of the quotient rule and the importance of considering the conditions where variables cannot be zero to avoid undefined results.
Frequently Asked Questions (FAQ)
-
Q: What if x = 0?
A: If x = 0, the expression x² ÷ x² becomes 0 ÷ 0, which is undefined in mathematics. There is no single defined answer for division by zero.
-
Q: Can we simplify x³ ÷ x² in the same way?
A: Yes, applying the quotient rule, x³ ÷ x² = x⁽³⁻²⁾ = x¹ = x (assuming x ≠ 0).
-
Q: What happens if the exponent in the denominator is larger than the exponent in the numerator?
A: For instance, x² ÷ x³ = x⁽²⁻³⁾ = x⁻¹ = 1/x (assuming x ≠ 0). The result will be a reciprocal, or a fraction with x in the denominator.
-
Q: Are there any real-world applications of simplifying expressions like x² ÷ x²?
A: While this specific example might not have an immediately obvious real-world application, the underlying principles of exponent rules and algebraic simplification are fundamental to various fields, including physics, engineering, and finance, in modelling and solving problems involving variables and rates of change.
Conclusion: Mastering Algebraic Simplification
Understanding the simplification of x² ÷ x² is not just about getting the answer of 1; it's about grasping the core principles of algebraic manipulation and the critical importance of considering the conditions under which a mathematical operation is defined. Mastering this seemingly simple problem provides a solid foundation for tackling more complex algebraic expressions and builds a deeper understanding of fundamental mathematical concepts. Remember the quotient rule of exponents, the zero exponent rule, and the crucial caveat that division by zero is undefined. By applying these principles and paying attention to detail, you can confidently simplify similar algebraic expressions and advance your mathematical skills. The ability to accurately and efficiently simplify algebraic expressions is an invaluable skill in many academic and professional pursuits.
Latest Posts
Latest Posts
-
What Is 100 M In Yards
Aug 26, 2025
-
The Graph Of A Function G Is Given
Aug 26, 2025
-
Five Times The Quotient Of Some Number And Ten
Aug 26, 2025
-
Elena Has 2 Fewer Hats Than Fran
Aug 26, 2025
-
A Solution Is Made By Dissolving
Aug 26, 2025
Related Post
Thank you for visiting our website which covers about X Squared Divided By X Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.