X Greater Than Or Equal To 2
faraar
Sep 15, 2025 · 6 min read
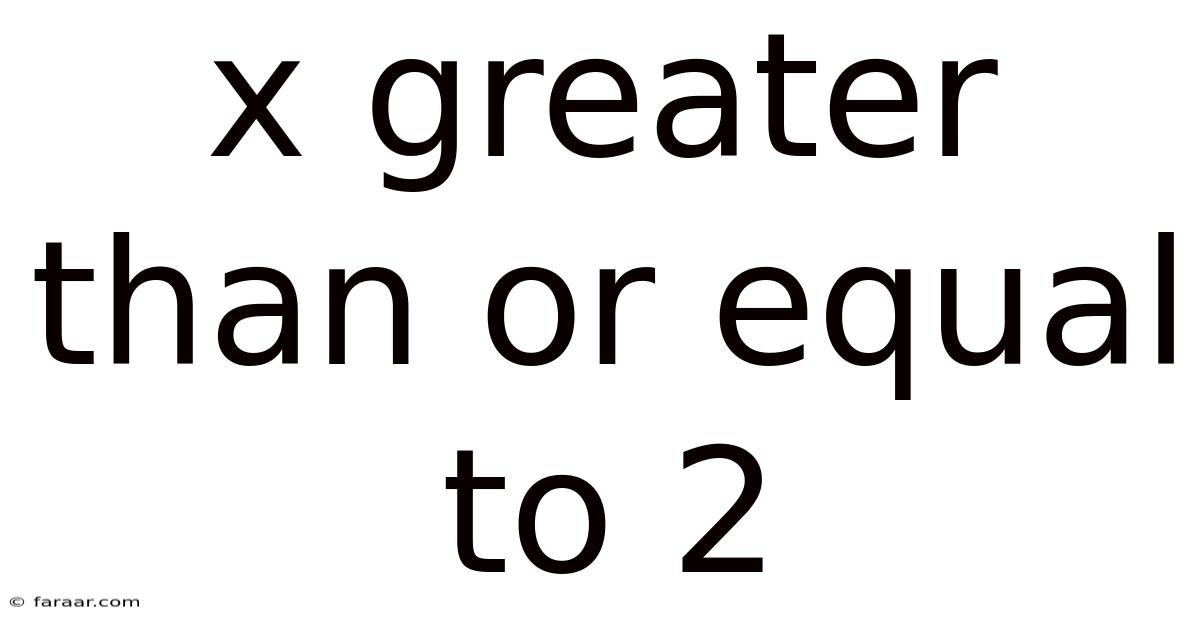
Table of Contents
Understanding "x ≥ 2": A Comprehensive Guide to Inequalities
The simple mathematical statement "x ≥ 2" represents an inequality, a fundamental concept in algebra and beyond. This article will explore this inequality in depth, explaining its meaning, how to represent it graphically and algebraically, and its applications in various mathematical contexts. We will also delve into solving inequalities involving "x ≥ 2" and address common questions and misconceptions surrounding this topic. Understanding inequalities is crucial for anyone pursuing further studies in mathematics, science, engineering, and even economics. This comprehensive guide aims to provide a solid foundation for mastering this important concept.
What Does "x ≥ 2" Mean?
The expression "x ≥ 2" is read as "x is greater than or equal to 2". This means that the variable x can represent any number that is either larger than 2 or exactly equal to 2. This is in contrast to an equation, which states that two expressions are equal. Inequalities, on the other hand, express a relationship of order between two expressions.
- Greater Than (>): This symbol indicates that one value is strictly larger than another. For example, 3 > 2 means 3 is greater than 2.
- Equal To (=): This symbol indicates that two values are identical.
- Greater Than or Equal To (≥): This combines the two previous symbols, indicating that one value is either larger than or equal to another. Therefore, x ≥ 2 means x can be 2, 3, 4, 5, 10, 100, or any other number greater than 2.
The key takeaway here is the inclusion of the equality. Unlike "x > 2", which excludes the value 2, "x ≥ 2" explicitly includes 2 as a possible solution. This seemingly small difference has significant consequences in how we represent and solve the inequality.
Representing "x ≥ 2" Graphically
Inequalities can be effectively visualized using number lines. To represent "x ≥ 2" on a number line:
- Draw a Number Line: Create a horizontal line with evenly spaced numbers.
- Locate 2: Find the point representing the number 2 on your number line.
- Mark the Point: Instead of just a point, draw a filled circle (or a square bracket) at 2. This indicates that 2 is included in the solution set.
- Shade the Region: Shade the portion of the number line to the right of 2. This represents all the numbers greater than 2.
This visual representation immediately conveys all the values that satisfy the inequality "x ≥ 2".
Algebraic Manipulation of Inequalities Involving "x ≥ 2"
Solving more complex inequalities often involves manipulating the expression to isolate the variable. The rules for manipulating inequalities are similar to those for equations, but with one crucial difference:
- Adding or Subtracting: You can add or subtract the same value from both sides of the inequality without changing the inequality sign. For example, if x ≥ 2, then x + 3 ≥ 5.
- Multiplying or Dividing by a Positive Number: You can multiply or divide both sides by the same positive number without changing the inequality sign. If x ≥ 2, then 2x ≥ 4.
- Multiplying or Dividing by a Negative Number: This is where the crucial difference lies. When multiplying or dividing by a negative number, you must reverse the inequality sign. For example, if x ≥ 2, then -x ≤ -2.
Let's illustrate with an example:
Solve the inequality 3x - 5 ≥ 7
- Add 5 to both sides: 3x ≥ 12
- Divide both sides by 3: x ≥ 4
The solution is x ≥ 4, meaning any value of x greater than or equal to 4 satisfies the original inequality.
Applications of "x ≥ 2" in Real-World Scenarios
Inequalities like "x ≥ 2" are not just abstract mathematical concepts; they have numerous real-world applications. Consider these examples:
- Age Restrictions: Many activities have age restrictions. If an amusement park ride requires riders to be at least 2 years old, we can represent this as age ≥ 2.
- Weight Limits: Trucks and other vehicles have weight limits. If a bridge has a weight limit of 2 tons, the weight of vehicles crossing it must satisfy weight ≥ 2 tons.
- Minimum Requirements: In many fields, minimum requirements are set. For example, a job might require at least 2 years of experience (experience ≥ 2 years).
- Pricing and Discounts: Discounts often apply when purchases meet a minimum value. A store might offer free shipping for orders exceeding $20 (order value ≥ $20).
Solving Compound Inequalities Involving "x ≥ 2"
A compound inequality involves multiple inequalities combined using "and" or "or". Let's examine a couple of examples:
-
Example 1 (AND): Solve the compound inequality: x ≥ 2 AND x < 5. This means we need values of x that satisfy both conditions simultaneously. The solution is 2 ≤ x < 5, which represents all numbers between 2 (inclusive) and 5 (exclusive).
-
Example 2 (OR): Solve the compound inequality: x ≥ 2 OR x ≤ 1. This means we need values of x that satisfy at least one of the conditions. The solution is x ≤ 1 OR x ≥ 2, which represents all numbers less than or equal to 1, or greater than or equal to 2.
Interval Notation
Another way to represent inequalities is using interval notation. Interval notation uses brackets and parentheses to denote the range of values included in the solution.
- [a, b]: Closed interval, including both a and b. Equivalent to a ≤ x ≤ b.
- (a, b): Open interval, excluding both a and b. Equivalent to a < x < b.
- [a, b): Half-open interval, including a but excluding b. Equivalent to a ≤ x < b.
- (a, b]: Half-open interval, excluding a but including b. Equivalent to a < x ≤ b.
For "x ≥ 2," the interval notation is [2, ∞), where ∞ represents infinity, indicating that the interval extends indefinitely to the right. The square bracket indicates that 2 is included in the solution set.
Frequently Asked Questions (FAQ)
Q: What's the difference between x ≥ 2 and x > 2?
A: x ≥ 2 includes the value 2 as a solution, while x > 2 does not. x ≥ 2 represents all numbers greater than or equal to 2, while x > 2 represents only numbers strictly greater than 2.
Q: Can I multiply both sides of an inequality by zero?
A: No. Multiplying by zero eliminates the inequality, leading to an invalid result.
Q: How do I solve inequalities with absolute values?
A: Inequalities involving absolute values require careful consideration of cases. For example, to solve |x| ≥ 2, you consider two cases: x ≥ 2 and x ≤ -2.
Conclusion
Understanding inequalities, especially expressions like "x ≥ 2," is a fundamental skill in mathematics. This article has explored the meaning, graphical representation, algebraic manipulation, real-world applications, and nuances of this inequality. By grasping these concepts, you'll be well-equipped to tackle more complex mathematical problems and apply these principles to diverse fields of study and real-world situations. Remember the key differences between > and ≥, the rules for manipulating inequalities, and the importance of using appropriate notation for clear communication of your solution. With practice and continued learning, mastering inequalities will become second nature.
Latest Posts
Latest Posts
-
Common Factors For 16 And 24
Sep 15, 2025
-
How Fast Is 4 Miles Per Hour
Sep 15, 2025
-
What To Do With Remainder In Long Division
Sep 15, 2025
-
2 3 Kg Is How Many Pounds
Sep 15, 2025
-
Mitochondria And Other Organelles Are Made Interphase Or Mitosis
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X Greater Than Or Equal To 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.