What Two Numbers Multiply To 36
faraar
Sep 22, 2025 · 5 min read
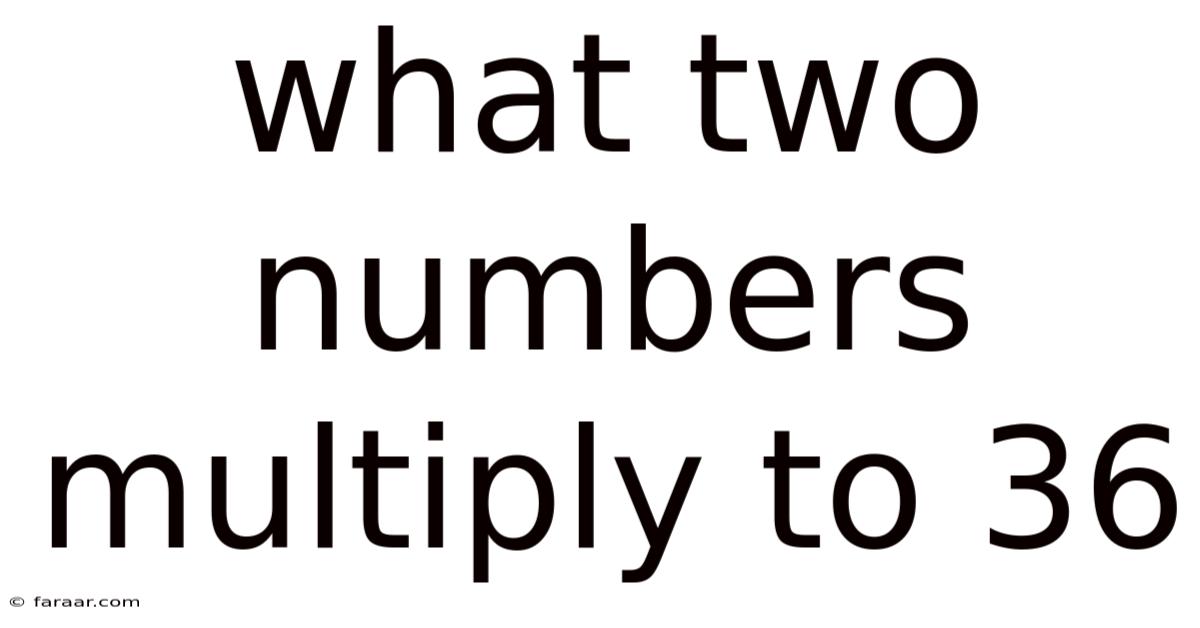
Table of Contents
What Two Numbers Multiply to 36? A Deep Dive into Factors and Multiplication
Finding two numbers that multiply to 36 might seem like a simple arithmetic problem, suitable only for elementary school. However, this seemingly basic question opens the door to a fascinating exploration of number theory, factorization, and the fundamental building blocks of mathematics. This article will delve into various ways to find these numbers, exploring different approaches and expanding our understanding of multiplication and factors. We'll cover simple methods, delve into prime factorization, and even touch upon more advanced mathematical concepts related to this seemingly straightforward problem.
Introduction: Understanding Factors and Multiplication
Before we jump into finding the pairs of numbers that multiply to 36, let's establish a firm foundation. Factors are numbers that divide evenly into a larger number without leaving a remainder. In other words, if you multiply two or more factors together, you get the original number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without leaving a remainder. This concept is crucial for understanding the different ways we can arrive at the solution to "what two numbers multiply to 36?"
Simple Methods: Listing and Trial and Error
The most straightforward way to find pairs of numbers that multiply to 36 is through a simple listing method combined with trial and error. We can start by listing all the factors of 36:
- 1 x 36
- 2 x 18
- 3 x 12
- 4 x 9
- 6 x 6
This method is systematic and relatively quick for smaller numbers like 36. However, as the target number increases, this process becomes more laborious. It's a great approach for building intuition and understanding the concept of factors.
Prime Factorization: The Building Blocks of Numbers
A more sophisticated and efficient method involves prime factorization. Prime numbers are whole numbers greater than 1 that have only two factors: 1 and themselves (e.g., 2, 3, 5, 7, 11...). Prime factorization is the process of expressing a number as the product of its prime factors. This method provides a unique and fundamental representation of any number.
Let's prime factorize 36:
- Start by dividing 36 by the smallest prime number, 2: 36 ÷ 2 = 18
- Divide 18 by 2: 18 ÷ 2 = 9
- Now, 9 is not divisible by 2, but it is divisible by the next prime number, 3: 9 ÷ 3 = 3
- Finally, 3 is a prime number.
Therefore, the prime factorization of 36 is 2 x 2 x 3 x 3, or 2² x 3². This prime factorization allows us to derive all possible pairs of factors that multiply to 36. We can combine these prime factors in various ways to form the pairs we found earlier:
- 2 x 18 (2 x (2 x 9) = 2 x (2 x 3 x 3) )
- 4 x 9 ( (2 x 2) x (3 x 3) )
- 6 x 6 ( (2 x 3) x (2 x 3) )
- 1 x 36 (1 x (2² x 3²) )
- 3 x 12 (3 x (2² x 3) )
This method is more powerful because it provides a structured approach, especially useful for larger numbers. It helps us systematically generate all possible factor pairs, ensuring we don't miss any.
Beyond Two Numbers: Exploring Multiple Factors
The initial question focused on finding two numbers that multiply to 36. However, we can expand this to explore combinations of more than two factors. Using the prime factorization (2² x 3²), we can see numerous possibilities:
- 2 x 2 x 9
- 2 x 3 x 6
- 2 x 3 x 3 x 2
- 3 x 3 x 4
- and many more...
This demonstrates that while finding two factors is a specific case, the broader understanding of prime factorization reveals a wealth of multiplicative combinations that yield 36.
Mathematical Applications: Expanding the Scope
Understanding factors and multiplication extends far beyond finding pairs of numbers that multiply to 36. These concepts are fundamental to various areas of mathematics:
- Algebra: Factoring polynomials relies on the same principles as factoring numbers. Identifying common factors is crucial for simplifying expressions and solving equations.
- Geometry: Area calculations often involve finding the product of dimensions (length and width). Understanding factors helps in determining possible dimensions of shapes given a specific area.
- Number Theory: Prime factorization is a cornerstone of number theory, a branch of mathematics that explores the properties and relationships of numbers. Concepts like greatest common divisors (GCD) and least common multiples (LCM) directly relate to factor analysis.
- Cryptography: Prime numbers and factorization play a vital role in modern cryptography, securing online transactions and communications.
Frequently Asked Questions (FAQ)
Q: Are there negative factors of 36?
A: Yes, absolutely! Since a negative number multiplied by a negative number results in a positive number, we can also have pairs like (-1) x (-36), (-2) x (-18), (-3) x (-12), (-4) x (-9), and (-6) x (-6). Remember, the question asks for numbers that multiply to 36, not just positive numbers that multiply to 36.
Q: What if the question asked for three numbers that multiply to 36?
A: Using prime factorization (2² x 3²), we can find various combinations: 2 x 2 x 9, 2 x 3 x 6, and more. The number of possibilities expands significantly when considering more than two factors.
Q: How does this relate to solving equations?
A: Finding numbers that multiply to a specific value is often a crucial step in solving quadratic equations and other polynomial equations. Factoring the equation helps in finding the roots or solutions.
Q: Are there any real-world applications of this concept?
A: Yes, numerous real-world situations involve finding factors. Examples include dividing resources equally, calculating areas and volumes, and even scheduling tasks efficiently.
Conclusion: Beyond the Simple Calculation
While the initial question – "What two numbers multiply to 36?" – might seem simplistic, its exploration reveals a rich tapestry of mathematical concepts and applications. From simple listing and trial and error to the powerful technique of prime factorization, the journey to understanding factors and multiplication provides a solid foundation for more advanced mathematical explorations. The seemingly straightforward problem of finding factors opens doors to algebra, geometry, number theory, and even cryptography, highlighting the interconnectedness and beauty of mathematics. Remember, even simple questions can lead to profound insights and understanding. So, the next time you encounter a similar problem, don't just look for the answer; explore the deeper mathematical principles involved.
Latest Posts
Latest Posts
-
What Is The Oxygen To Sulfur Mass Ratio Of Sulfur Dioxide
Sep 22, 2025
-
Click On The Measure Of The Angle
Sep 22, 2025
-
Leave Your Answer In Simplest Radical Form
Sep 22, 2025
-
How To Solve For A Variable In The Exponent
Sep 22, 2025
-
Calculate The Value Of The Rate Constant K
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Two Numbers Multiply To 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.