What Percent Is 25 Of 100
faraar
Aug 26, 2025 · 5 min read
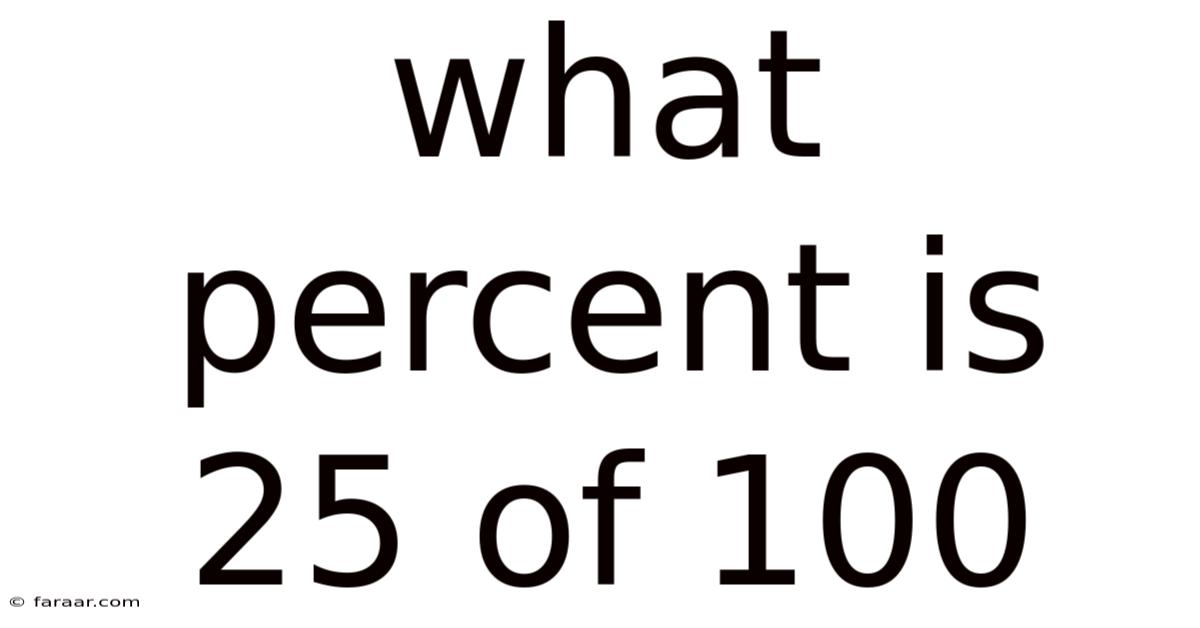
Table of Contents
What Percent is 25 of 100? A Deep Dive into Percentages
Understanding percentages is a fundamental skill in mathematics with broad applications in everyday life, from calculating discounts and tax to analyzing data and understanding statistics. This article will not only answer the question, "What percent is 25 of 100?" but will also delve into the underlying concepts, providing a comprehensive understanding of percentages and how to calculate them. We'll explore different methods, provide real-world examples, and address frequently asked questions.
Introduction: Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin phrase "per centum," meaning "out of a hundred." Therefore, 25% literally means 25 out of 100. This seemingly simple concept forms the basis for numerous calculations across various fields.
What Percent is 25 of 100? The Answer and its Calculation
The answer is straightforward: 25 of 100 is 25%.
This is because a percentage represents a portion of a whole. In this case, the whole is 100, and the portion we're interested in is 25. To calculate the percentage, we use the following formula:
(Part / Whole) * 100%
Substituting the values:
(25 / 100) * 100% = 25%
This simple calculation confirms our initial answer. However, let's explore this further by examining different approaches and scenarios.
Method 1: Using the Formula (Part/Whole) x 100%
This is the most common and widely used method for calculating percentages. It's straightforward and works for any scenario where you know the part and the whole.
- Identify the part: This is the number you want to express as a percentage of the whole (in our example, 25).
- Identify the whole: This is the total amount or the base value (in our example, 100).
- Apply the formula: Divide the part by the whole and multiply the result by 100%.
This method is reliable and easily adaptable to various percentage problems.
Method 2: Using Proportions
Another way to approach this problem is through the use of proportions. A proportion is a statement that two ratios are equal. We can set up a proportion as follows:
25/100 = x/100
where 'x' represents the percentage we want to find. To solve for 'x', we can cross-multiply:
25 * 100 = 100 * x
2500 = 100x
x = 2500 / 100
x = 25
Therefore, x = 25%, demonstrating the same result as the previous method.
Method 3: Using Decimal Conversion
We can also convert the fraction 25/100 to a decimal and then multiply by 100% to find the percentage.
25/100 = 0.25
0.25 * 100% = 25%
This method highlights the relationship between decimals and percentages. Every percentage can be represented as a decimal, and vice versa.
Real-World Applications: Why Understanding Percentages Matters
Understanding percentages is crucial for numerous everyday situations:
- Shopping: Calculating discounts, sales tax, and tips. For example, a 25% discount on a $100 item means you save $25.
- Finance: Understanding interest rates on loans and investments, calculating returns on investments, and analyzing financial statements.
- Science and Statistics: Representing data in charts and graphs, interpreting statistical results, and making comparisons.
- Everyday Life: Understanding percentages in recipes, calculating proportions for mixing ingredients, and interpreting survey results.
Beyond the Basics: Calculating Other Percentages
While the example of 25% of 100 is relatively simple, the principles can be applied to more complex scenarios. Let's consider a few examples:
- What is 15% of 50? Using the formula: (15/100) * 50 = 7.5
- What is 75% of 200? Using the formula: (75/100) * 200 = 150
- What percent is 30 of 150? Using the formula: (30/150) * 100% = 20%
These examples illustrate how versatile the percentage formula is. The core principle remains the same: divide the part by the whole and multiply by 100%.
Explanation of Scientific Principles
The calculation of percentages is based on the fundamental concept of ratios and proportions. A ratio compares two quantities, while a proportion states that two ratios are equal. Percentages are simply a specific type of ratio, expressed as a fraction of 100. This aligns with the fundamental principles of arithmetic and algebra. The ability to manipulate ratios and proportions is crucial for problem-solving in various scientific and mathematical contexts.
Frequently Asked Questions (FAQ)
- What if the 'whole' is not 100? The formula (Part / Whole) * 100% works regardless of the value of the whole. The calculation will yield the percentage that the part represents of the whole.
- How can I calculate the percentage increase or decrease? To calculate percentage increase, find the difference between the new value and the original value, divide the difference by the original value, and multiply by 100%. Percentage decrease is calculated similarly, but the difference is negative.
- What are some common percentage errors to avoid? Common errors include incorrectly identifying the 'part' and 'whole,' performing calculations in the wrong order, and misinterpreting decimal places. Carefully checking your work is essential.
Conclusion: Mastering Percentages for a Brighter Future
Understanding percentages is a crucial life skill, enabling us to interpret data, make informed decisions, and confidently navigate various aspects of our daily lives. While seemingly simple, a solid grasp of percentage calculations opens doors to more advanced mathematical concepts and applications. By mastering the fundamental concepts and methods outlined in this article, you'll be well-equipped to tackle percentage problems with confidence and accuracy. Remember the basic formula: (Part / Whole) * 100%, and practice regularly to solidify your understanding. With consistent effort, you’ll master this essential mathematical skill and enhance your problem-solving capabilities across diverse areas.
Latest Posts
Latest Posts
-
How To Construct Relative Frequency Distribution
Aug 26, 2025
-
What Is The Word Count For Common App Essay
Aug 26, 2025
-
Can You Use A Calculator On The Asvab 2024
Aug 26, 2025
-
Find Two Consecutive Integers Whose Sum Is 35
Aug 26, 2025
-
3 Billion Divided By 300 Million
Aug 26, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 25 Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.