What Is Three Quarters As A Decimal
faraar
Aug 28, 2025 · 6 min read
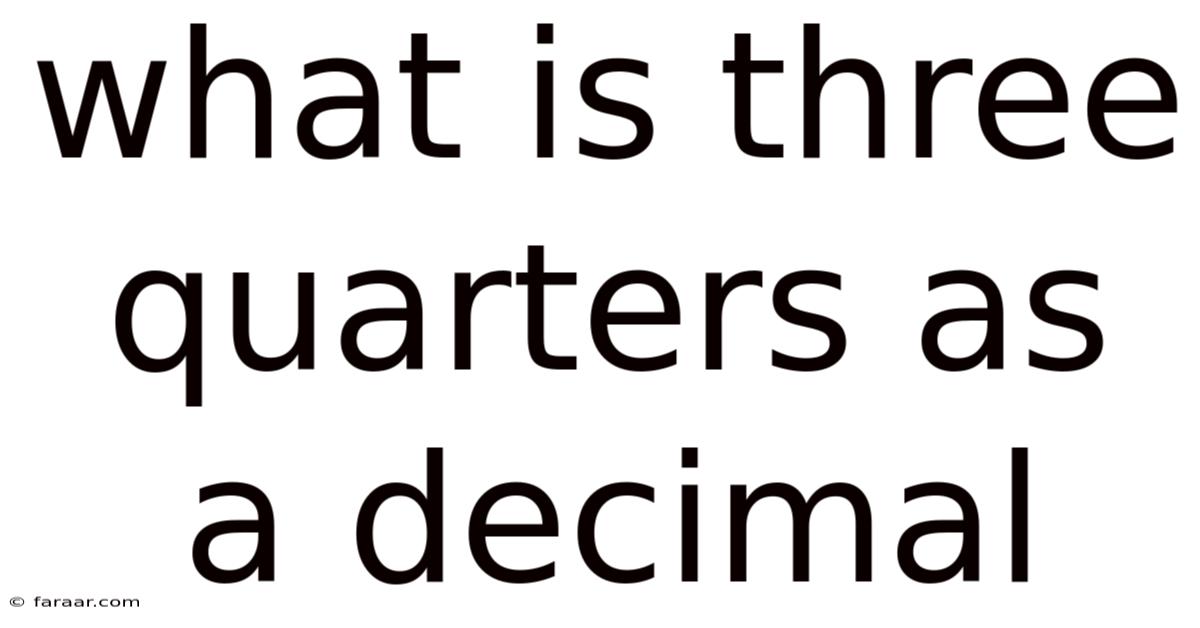
Table of Contents
What is Three Quarters as a Decimal? A Comprehensive Guide
Understanding fractions and their decimal equivalents is fundamental to mathematics. This comprehensive guide delves into the conversion of three-quarters (¾) into its decimal form, exploring the underlying principles and providing various methods for achieving this conversion. We will also examine related concepts and answer frequently asked questions to solidify your understanding. This guide aims to be your complete resource on this seemingly simple yet crucial mathematical concept.
Introduction: Fractions and Decimals
Before diving into the specifics of converting three-quarters to a decimal, let's establish a foundational understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: a numerator (the top number) and a denominator (the bottom number). For example, in the fraction ¾, 3 is the numerator and 4 is the denominator. This signifies three parts out of a total of four equal parts.
A decimal, on the other hand, represents a fraction where the denominator is a power of 10 (10, 100, 1000, etc.). Decimals use a decimal point to separate the whole number part from the fractional part. For example, 0.5 is a decimal representing one-half (1/2), and 0.75 represents three-quarters (¾).
Method 1: Direct Division
The most straightforward method to convert a fraction to a decimal is through direct division. This involves dividing the numerator by the denominator. In the case of three-quarters (¾), we divide 3 by 4:
3 ÷ 4 = 0.75
Therefore, three-quarters as a decimal is 0.75.
Method 2: Converting to a Denominator of 100
Another effective approach involves converting the fraction to an equivalent fraction with a denominator of 100. This is particularly helpful when dealing with percentages, as percentages are essentially fractions with a denominator of 100.
To convert ¾ to a fraction with a denominator of 100, we need to find a number that, when multiplied by 4, equals 100. This number is 25 (4 x 25 = 100). Since we multiply the denominator by 25, we must also multiply the numerator by 25 to maintain the fraction's value:
(3 x 25) / (4 x 25) = 75/100
A fraction with a denominator of 100 can be easily expressed as a decimal. The numerator becomes the digits after the decimal point, with the number of digits corresponding to the number of zeros in the denominator (in this case, two zeros). Thus, 75/100 = 0.75.
Method 3: Using a Calculator
Modern calculators provide a convenient tool for converting fractions to decimals. Simply enter the fraction as 3/4 and press the equals button (=). The calculator will automatically perform the division and display the decimal equivalent, which is 0.75.
Understanding the Decimal Representation: Place Value
The decimal representation 0.75 reveals important information about the value of three-quarters. The digit '7' represents seven-tenths (7/10), while the digit '5' represents five-hundredths (5/100). Adding these together, we get:
7/10 + 5/100 = 70/100 + 5/100 = 75/100 = ¾
This illustrates how the decimal system uses place value to represent fractions with denominators that are powers of 10.
Three-Quarters as a Percentage
Since decimals and percentages are closely related, it's beneficial to express three-quarters as a percentage. A percentage is a fraction with a denominator of 100, expressed using the "%" symbol. We already established that ¾ is equivalent to 75/100. Therefore:
75/100 = 75%
Real-World Applications of Three-Quarters
Understanding the decimal representation of three-quarters has numerous real-world applications:
- Finance: Calculating discounts, interest rates, or portions of payments often involves fractions and their decimal equivalents.
- Measurement: In various fields like construction, cooking, and engineering, precise measurements frequently require converting fractions to decimals for calculations.
- Data Analysis: Representing data in graphs and charts sometimes requires converting fractions into decimals for clearer visual representation.
- Everyday Calculations: Dividing quantities or sharing items equally may involve fractions that need to be converted to decimals for easier calculations.
Expanding on Fractions and Decimals: Further Exploration
This section explores more complex aspects of fractions and decimals, building on the understanding of converting three-quarters to its decimal equivalent.
- Recurring Decimals: Not all fractions result in terminating decimals like 0.75. Some fractions produce recurring decimals, where one or more digits repeat infinitely. For example, 1/3 equals 0.3333... Understanding these repeating patterns is crucial in advanced mathematics.
- Significant Figures and Rounding: When working with decimals, especially those derived from fractions, the concept of significant figures and rounding becomes essential for accuracy and practicality. Depending on the context, you may need to round a decimal to a specific number of decimal places.
- Converting Decimals to Fractions: The reverse process—converting decimals back into fractions—is equally important and involves understanding place value and simplifying fractions to their lowest terms.
Frequently Asked Questions (FAQ)
Q1: Is 0.75 the only decimal representation of three-quarters?
A1: Yes, 0.75 is the exact decimal representation of three-quarters. There are no other equivalent decimal representations.
Q2: Can all fractions be converted to terminating decimals?
A2: No. Only fractions with denominators that can be expressed as 2<sup>m</sup> x 5<sup>n</sup> (where 'm' and 'n' are non-negative integers) will result in terminating decimals. Fractions with other denominators will produce recurring decimals.
Q3: What if I get a long decimal when dividing?
A3: If you're using long division and the decimal appears to go on indefinitely, it's likely a recurring decimal. You may need to round the decimal to a suitable number of significant figures based on the context of your calculation.
Q4: Why is understanding this conversion important?
A4: Converting fractions to decimals is a fundamental skill in mathematics that underpins numerous applications in various fields. It's essential for accurate calculations, data representation, and problem-solving in everyday life and professional settings.
Conclusion: Mastering the Conversion
Converting three-quarters (¾) to its decimal equivalent (0.75) is a simple yet crucial mathematical skill. Understanding the different methods – direct division, converting to a denominator of 100, and using a calculator – allows you to choose the most efficient approach depending on the situation. Moreover, grasping the underlying principles of fractions, decimals, and place value provides a robust foundation for tackling more complex mathematical problems in the future. This comprehensive guide has equipped you with not only the answer but also the knowledge and understanding to confidently approach similar conversions and further explore the fascinating world of numbers. Remember that practice is key to mastering these concepts. So, grab your calculator, work through some examples, and build your mathematical confidence!
Latest Posts
Latest Posts
-
A Negative Divided By A Positive Is A
Aug 29, 2025
-
Finding The Equation Of A Secant Line
Aug 29, 2025
-
What Happens When You Divide A Negative By A Positive
Aug 29, 2025
-
Complete The Sentences To Summarize The Article
Aug 29, 2025
-
Which Of The Following Is A Buffer System
Aug 29, 2025
Related Post
Thank you for visiting our website which covers about What Is Three Quarters As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.