What Is The Greatest Common Factor Of 17 And 51
faraar
Sep 12, 2025 · 6 min read
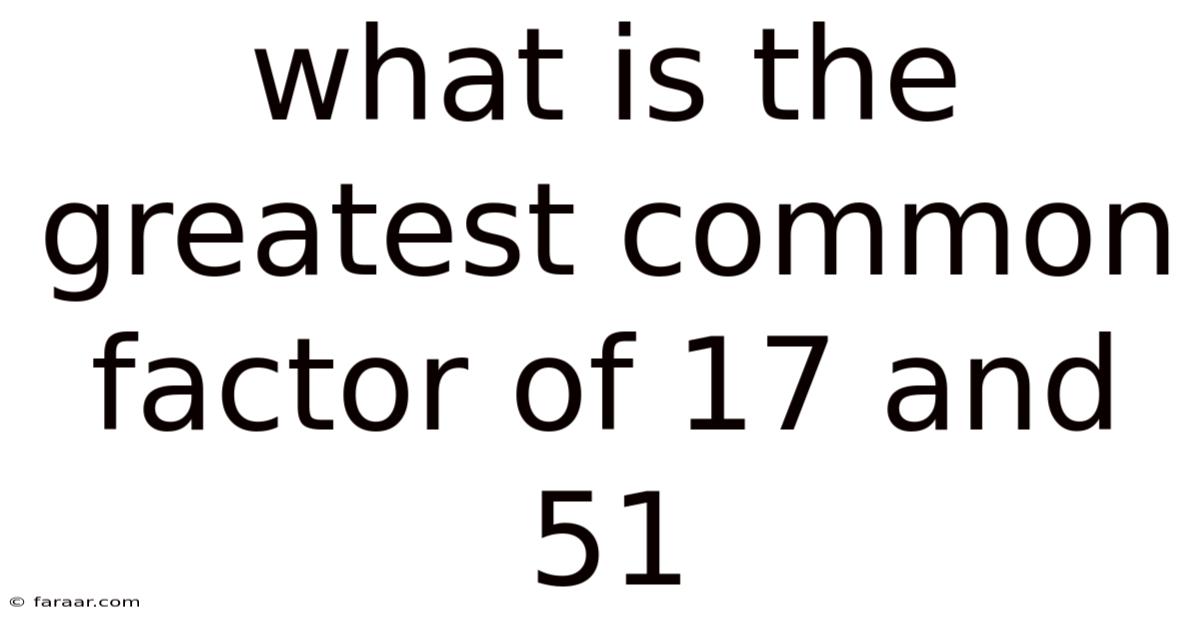
Table of Contents
Unlocking the Mystery: Finding the Greatest Common Factor (GCF) of 17 and 51
Finding the greatest common factor (GCF) might sound intimidating, but it's a fundamental concept in mathematics with practical applications far beyond the classroom. This article dives deep into determining the GCF of 17 and 51, exploring various methods and explaining the underlying principles. We'll not only find the answer but also equip you with a solid understanding of how to tackle similar problems, regardless of the numbers involved. Understanding GCF is crucial for simplifying fractions, solving algebraic equations, and even in more advanced mathematical fields.
Understanding Greatest Common Factor (GCF)
Before we delve into the specifics of 17 and 51, let's establish a clear understanding of what the greatest common factor actually is. The GCF of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. In simpler terms, it's the biggest number that's a factor of all the numbers in question.
For example, let's consider the numbers 12 and 18. The factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6. Therefore, the GCF of 12 and 18 is 6.
Method 1: Prime Factorization
Prime factorization is a powerful technique for finding the GCF of any set of numbers. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
Let's apply this method to find the GCF of 17 and 51:
-
Prime Factorization of 17: 17 is a prime number itself. Its only factors are 1 and 17. Therefore, the prime factorization of 17 is simply 17.
-
Prime Factorization of 51: We can start by dividing 51 by the smallest prime number, 2. Since 51 is an odd number, it's not divisible by 2. Let's try the next prime number, 3. 51 divided by 3 is 17. And 17, as we know, is a prime number. Therefore, the prime factorization of 51 is 3 x 17.
Now, we look for the common prime factors in both factorizations. Both 17 and 51 share the prime factor 17. There are no other common prime factors.
Therefore, the GCF of 17 and 51 is 17.
Method 2: Listing Factors
This method is straightforward but can become cumbersome with larger numbers. We list all the factors of each number and then identify the largest factor they share.
- Factors of 17: 1, 17
- Factors of 51: 1, 3, 17, 51
Comparing the two lists, we see that the common factors are 1 and 17. The greatest of these common factors is 17. Thus, the GCF of 17 and 51 is 17.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 17 and 51:
- Start with the larger number (51) and the smaller number (17).
- Subtract the smaller number from the larger number: 51 - 17 = 34.
- Now we have 17 and 34. Repeat the process: 34 - 17 = 17.
- Now we have 17 and 17. The numbers are equal.
Therefore, the GCF of 17 and 51 is 17.
Why Understanding GCF is Important
The concept of the greatest common factor isn't just an abstract mathematical exercise. It has numerous real-world applications:
-
Simplifying Fractions: Finding the GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 51/17 can be simplified by dividing both the numerator and denominator by their GCF (17), resulting in the simplified fraction 3/1 or simply 3.
-
Algebra: GCF is essential in factoring algebraic expressions. Being able to find the GCF allows for simplification and solving equations.
-
Geometry: GCF plays a role in solving geometric problems involving area and perimeter calculations.
-
Real-World Problem Solving: Imagine you have 51 apples and 17 oranges. You want to divide them into identical bags, with each bag containing the same number of apples and oranges. The GCF (17) tells you that you can create 17 bags, each containing 3 apples and 1 orange.
Expanding Our Understanding: Beyond Two Numbers
The methods discussed above can be extended to find the GCF of more than two numbers. For prime factorization, you would find the prime factorization of each number and then identify the common prime factors raised to the lowest power. For the Euclidean algorithm, you would apply it iteratively to pairs of numbers until you find the GCF of the entire set.
Frequently Asked Questions (FAQ)
Q: Is the GCF always one of the original numbers?
A: Not necessarily. The GCF can be one of the original numbers, but it's not always the case. For instance, the GCF of 12 and 18 is 6, which is neither 12 nor 18. However, in the case of 17 and 51, the GCF (17) is one of the original numbers.
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they share no common factors other than 1.
Q: Are there any online tools or calculators to find the GCF?
A: Yes, many online calculators and tools can calculate the GCF of numbers. These can be helpful for verifying your work or for dealing with larger numbers. However, understanding the underlying methods is crucial for a deeper grasp of the concept.
Conclusion
Finding the greatest common factor of 17 and 51, which is 17, is not only a straightforward mathematical exercise but also a gateway to understanding a fundamental concept with broad applications. We've explored three different methods—prime factorization, listing factors, and the Euclidean algorithm—each providing a valuable perspective on how to determine the GCF. Mastering these techniques equips you with essential skills for simplifying fractions, solving algebraic equations, and tackling various real-world problems. Remember, the key is not just to find the answer but to understand the why behind the calculation. This understanding will serve you well in your mathematical journey. Keep practicing, and you'll find that GCF problems become increasingly easier and more intuitive.
Latest Posts
Latest Posts
-
Sum To Infinity Of A Geometric Series
Sep 12, 2025
-
How To Know If Function Is One To One
Sep 12, 2025
-
4x 2y 6 In Slope Intercept Form
Sep 12, 2025
-
Equation Of A Line That Is Parallel To
Sep 12, 2025
-
What Are The Common Factors Of 12 And 20
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is The Greatest Common Factor Of 17 And 51 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.