What Is The Gcf Of 9 And 21
faraar
Sep 17, 2025 · 6 min read
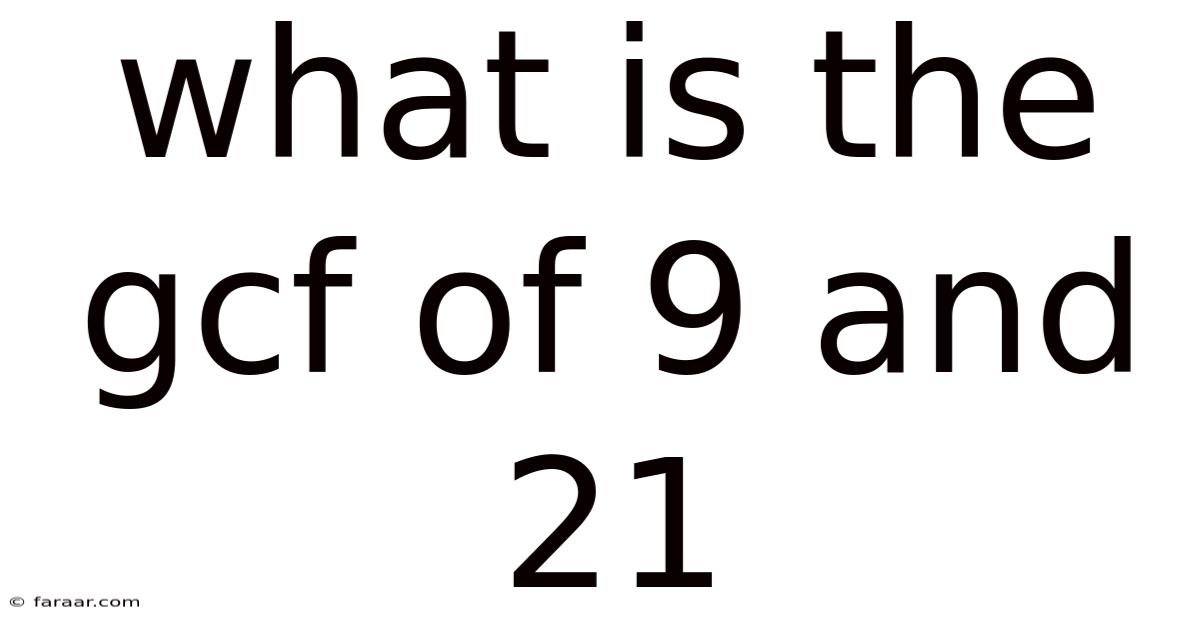
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 9 and 21: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles of GCF calculation unlocks a deeper appreciation of number theory and its applications in various fields, from cryptography to computer science. This comprehensive guide will not only show you how to find the GCF of 9 and 21 but also explore the different methods, explain the underlying mathematical concepts, and provide you with a solid foundation in this important area of mathematics.
Introduction: What is the Greatest Common Factor (GCF)?
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without any remainder. Understanding GCF is crucial in simplifying fractions, solving algebraic equations, and various other mathematical operations. This article focuses on finding the GCF of 9 and 21, illustrating several methods along the way.
Method 1: Listing Factors
This is the most straightforward method, especially for smaller numbers like 9 and 21. We start by listing all the factors of each number:
- Factors of 9: 1, 3, 9
- Factors of 21: 1, 3, 7, 21
Now, we identify the common factors—the numbers that appear in both lists: 1 and 3. The greatest of these common factors is 3. Therefore, the GCF of 9 and 21 is 3.
Method 2: Prime Factorization
Prime factorization is a more powerful method that works well for larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
- Prime factorization of 9: 3 x 3 = 3²
- Prime factorization of 21: 3 x 7
Now, we identify the common prime factors. Both 9 and 21 share a single factor of 3. To find the GCF, we multiply the common prime factors together. In this case, the GCF is simply 3.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers, particularly useful for larger numbers where listing factors becomes cumbersome. The algorithm is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. We repeatedly apply this principle until we reach a point where the remainder is 0. The last non-zero remainder is the GCF.
Let's apply the Euclidean algorithm to 9 and 21:
- Divide the larger number (21) by the smaller number (9): 21 ÷ 9 = 2 with a remainder of 3.
- Replace the larger number with the remainder: Now we find the GCF of 9 and 3.
- Divide the larger number (9) by the smaller number (3): 9 ÷ 3 = 3 with a remainder of 0.
- Since the remainder is 0, the GCF is the last non-zero remainder, which is 3.
Therefore, the GCF of 9 and 21 using the Euclidean algorithm is 3.
Explanation of the Euclidean Algorithm: A Deeper Dive
The Euclidean algorithm's efficiency stems from its iterative nature. The process relies on the property that if a and b are two integers, and r is the remainder when a is divided by b, then GCF(a, b) = GCF(b, r). This property is crucial because it allows us to reduce the problem of finding the GCF of two larger numbers to finding the GCF of a smaller pair of numbers. This iterative reduction continues until we reach a point where one of the numbers is 0, at which point the other number is the GCF. The algorithm's efficiency makes it particularly suitable for implementation in computer programs for finding the GCF of very large numbers.
Applications of the Greatest Common Factor
The GCF finds widespread application across various mathematical and computational fields:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 21/9 can be simplified by dividing both the numerator and the denominator by their GCF, which is 3, resulting in the simplified fraction 7/3.
-
Solving Linear Diophantine Equations: These equations involve finding integer solutions to equations of the form ax + by = c, where a, b, and c are integers. The GCF of a and b plays a crucial role in determining whether a solution exists and in finding the solutions.
-
Cryptography: GCF calculations are fundamental to various cryptographic algorithms, including the RSA algorithm, which is widely used for secure communication over the internet.
-
Computer Science: The Euclidean algorithm and other GCF-related techniques are used in various computer algorithms for tasks such as finding the least common multiple (LCM) of numbers, simplifying fractions in computer-aided design (CAD) software, and optimizing computational processes.
Frequently Asked Questions (FAQ)
-
What is the difference between GCF and LCM? The greatest common factor (GCF) is the largest number that divides both numbers without a remainder, while the least common multiple (LCM) is the smallest number that is a multiple of both numbers. They are related by the formula: LCM(a, b) x GCF(a, b) = a x b.
-
Can the GCF of two numbers be 1? Yes, if two numbers are relatively prime (meaning they share no common factors other than 1), their GCF is 1. For example, the GCF of 9 and 10 is 1.
-
How can I find the GCF of more than two numbers? You can extend the methods described above. For prime factorization, you find the prime factors of each number and identify the common prime factors. For the Euclidean algorithm, you can iteratively find the GCF of pairs of numbers until you find the GCF of all numbers.
-
Why is the Euclidean algorithm efficient? The Euclidean algorithm's efficiency stems from its ability to reduce the problem size rapidly. At each step, the numbers involved become smaller, leading to a quick convergence to the GCF, especially for large numbers.
Conclusion: Mastering the GCF
Finding the greatest common factor of 9 and 21, as we've demonstrated, is a straightforward process using various methods. However, understanding the underlying principles and exploring different techniques allows for a deeper grasp of number theory and its practical applications. Whether you're using the listing factors method, prime factorization, or the powerful Euclidean algorithm, the GCF calculation is a fundamental skill in mathematics with implications that extend far beyond basic arithmetic. The journey into understanding GCF not only equips you with problem-solving skills but also provides a foundation for appreciating the elegance and utility of fundamental mathematical concepts. By mastering these concepts, you’ll unlock a deeper understanding of the building blocks of mathematics and its influence on various fields.
Latest Posts
Latest Posts
-
How To Find Leading Coefficient Of Polynomial
Sep 17, 2025
-
How To Start A Good College Essay
Sep 17, 2025
-
What Happens If You Fail A Midterm In College
Sep 17, 2025
-
What Two Numbers Multiply To 32
Sep 17, 2025
-
Borrow 50 From Mom And Dad Answer
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 9 And 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.