What Is One Third Of A Half
faraar
Sep 09, 2025 · 7 min read
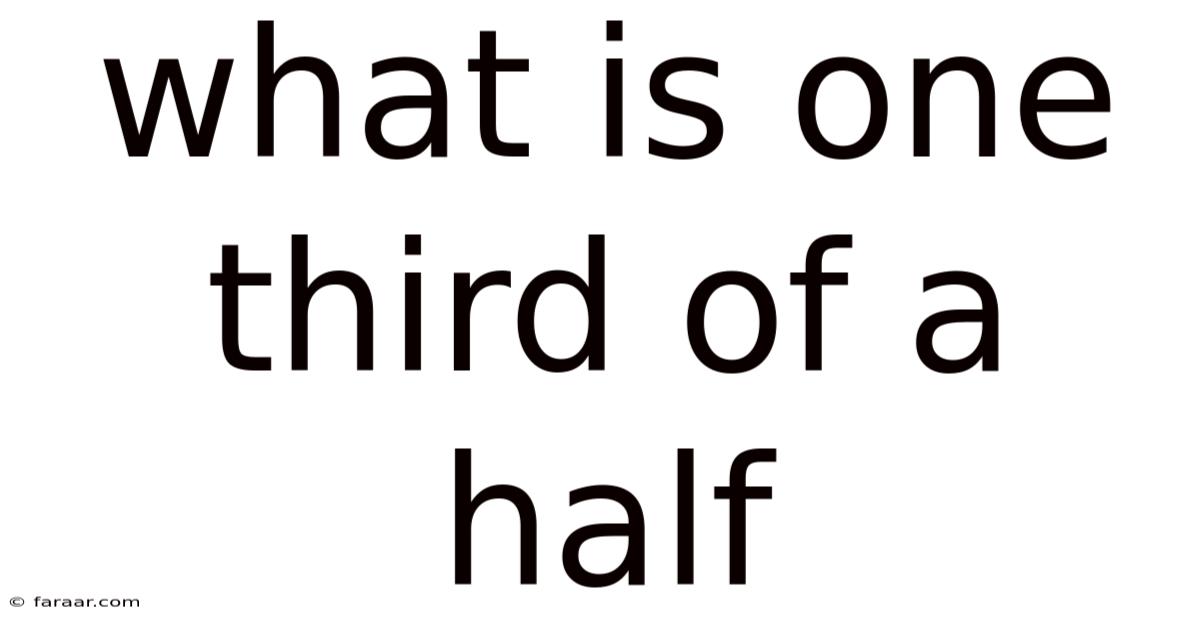
Table of Contents
What is One Third of a Half? Unraveling Fractions and Their Applications
This article explores the seemingly simple question, "What is one third of a half?", delving into the fundamental concepts of fractions, their representation, and practical applications. Understanding this seemingly basic calculation is crucial for grasping more complex mathematical concepts and for solving real-world problems involving proportions and ratios. We'll move beyond the simple answer to explore the underlying principles and illustrate the concept with various examples. By the end, you'll not only know the answer but also understand why it's the answer, enhancing your understanding of fractional arithmetic.
Understanding Fractions: A Quick Refresher
Before diving into the core question, let's revisit the basics of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/2 (one-half), the numerator is 1, and the denominator is 2, meaning we have one out of two equal parts of a whole.
Calculating One Third of a Half: The Step-by-Step Approach
Now, let's tackle the main question: What is one third of a half? This involves two steps:
-
Understanding "of" in mathematical terms: In mathematics, "of" often signifies multiplication. Therefore, "one third of a half" translates to (1/3) x (1/2).
-
Multiplying Fractions: To multiply fractions, we simply multiply the numerators together and the denominators together. In this case:
(1/3) x (1/2) = (1 x 1) / (3 x 2) = 1/6
Therefore, one third of a half is 1/6.
Visualizing the Calculation: A Pictorial Representation
Visual aids can greatly enhance understanding, especially when dealing with fractions. Imagine a circle representing a whole.
-
Half: Divide the circle in half. You now have two equal halves. Shade one of these halves.
-
One Third of a Half: Now, take that shaded half and divide it into three equal parts. Shade one of these three parts. You'll see that this shaded portion represents 1/6 of the original circle.
This visual representation reinforces the mathematical calculation and provides a concrete understanding of the concept.
Different Representations of 1/6: Exploring Equivalent Fractions
It's important to understand that 1/6 is just one way to represent this fraction. There are other equivalent fractions that represent the same value. Equivalent fractions are fractions that have the same value, even though they look different. They can be obtained by multiplying or dividing both the numerator and the denominator by the same number (except zero).
For instance, if we multiply both the numerator and the denominator of 1/6 by 2, we get 2/12. If we multiply by 3, we get 3/18, and so on. All these fractions—1/6, 2/12, 3/18, etc.—represent the same portion of a whole.
Beyond the Calculation: Applications in Real Life
Understanding fractions and their manipulations isn't merely an academic exercise. It's a fundamental skill with broad applications in everyday life:
-
Cooking and Baking: Recipes often require precise measurements using fractions. Understanding fractions is crucial for accurate conversions and consistent results. For instance, a recipe might call for 1/3 of a cup of sugar, and knowing how to calculate fractions becomes essential for accurate measuring.
-
Construction and Engineering: In construction and engineering, precise measurements are paramount. Fractions are extensively used in blueprints and calculations, ensuring that structures are built to specification. Calculating distances, angles, and material quantities often relies heavily on fractional arithmetic.
-
Finance and Budgeting: Managing personal finances involves dealing with fractions and percentages. Calculating interest rates, discounts, and taxes requires a strong understanding of fractional calculations. For example, understanding how much a 1/3 discount reduces the price of an item is a direct application of these skills.
-
Data Analysis and Statistics: Fractions and proportions play a crucial role in analyzing data and interpreting statistics. Presenting findings often involves expressing quantities as fractions or percentages, providing a clearer understanding of the overall picture.
-
Science and Medicine: Scientific experiments and medical dosages often involve precise measurements and calculations using fractions. Accuracy in these areas is critical for safe and effective outcomes. Consider the precise measurement of medication dosages or the exact quantities of chemicals needed in a lab setting.
Decimals and Percentages: Alternative Representations
While fractions are a powerful way to represent parts of a whole, decimals and percentages offer alternative representations. To convert a fraction to a decimal, we simply divide the numerator by the denominator:
1/6 = 1 ÷ 6 ≈ 0.1667
To convert a fraction to a percentage, we multiply the decimal by 100:
0.1667 x 100 = 16.67%
Therefore, 1/6 is approximately equal to 0.1667 or 16.67%. Understanding these different representations helps in comparing and contrasting quantities expressed in various formats.
Expanding on Fractional Arithmetic: More Complex Scenarios
The calculation of "one third of a half" serves as a springboard to explore more intricate fractional calculations. Here are a few examples:
-
Adding and Subtracting Fractions: To add or subtract fractions, they must have the same denominator (a common denominator). If they don't, you need to find a common denominator before performing the operation.
-
Dividing Fractions: Dividing fractions involves inverting (flipping) the second fraction and then multiplying. For example, (1/2) ÷ (1/3) = (1/2) x (3/1) = 3/2 = 1 1/2.
-
Fractions involving mixed numbers: Mixed numbers combine a whole number and a fraction (e.g., 1 1/2). To perform calculations with mixed numbers, it's often easier to convert them to improper fractions (where the numerator is larger than the denominator) before proceeding with the calculation.
Mastering these concepts opens up the door to solving a wider range of problems involving fractions.
Addressing Common Misconceptions
Several common misconceptions surround fractions, particularly when dealing with operations. Addressing these misunderstandings is crucial for a solid grasp of the concept.
-
Adding numerators and denominators directly: A frequent mistake is to add (or subtract) the numerators and denominators directly. This is incorrect. Fractions must have a common denominator before addition or subtraction.
-
Multiplying only the numerators or denominators: Similarly, simply multiplying the numerators or denominators independently is also wrong. Both numerators and denominators must be multiplied when performing fraction multiplication.
Frequently Asked Questions (FAQ)
Q: Why is "one third of a half" not equal to one fifth?
A: This is a common misconception. "Of" signifies multiplication, not addition. Adding one third and one half would be (1/3) + (1/2) = 5/6, which is different from 1/6.
Q: Can I use a calculator to solve this?
A: Yes, most calculators can handle fraction calculations. However, understanding the underlying principles is crucial for broader mathematical understanding.
Q: What are some real-world applications beyond those already mentioned?
A: The applications are limitless! Think about scaling recipes, dividing inheritance, calculating material needs for a DIY project, or even understanding proportions in artwork.
Q: How can I improve my understanding of fractions?
A: Practice is key! Work through various problems, use visual aids, and seek clarification when needed. Online resources and educational materials can provide additional support.
Conclusion: Embracing the Power of Fractions
Understanding the calculation "what is one third of a half?" is far more than just solving a simple mathematical problem. It's about grasping the fundamental concepts of fractions, their representation, and their wide-ranging applications in various aspects of life. By mastering fractional arithmetic, you equip yourself with a vital tool for problem-solving, critical thinking, and a deeper appreciation for the mathematical world around us. Remember that consistent practice and exploration of diverse applications will further solidify your understanding and confidence in tackling increasingly complex fractional calculations.
Latest Posts
Latest Posts
-
Is The Square Root Of 27 A Rational Number
Sep 09, 2025
-
Best Ways To Introduce A Quote
Sep 09, 2025
-
4 5 To The Power Of 3
Sep 09, 2025
-
Controls What Goes In And Out Of The Cell
Sep 09, 2025
-
Is Calm Before The Storm Real
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about What Is One Third Of A Half . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.