What Is Half Of 3 4 In A Fraction
faraar
Sep 15, 2025 · 5 min read
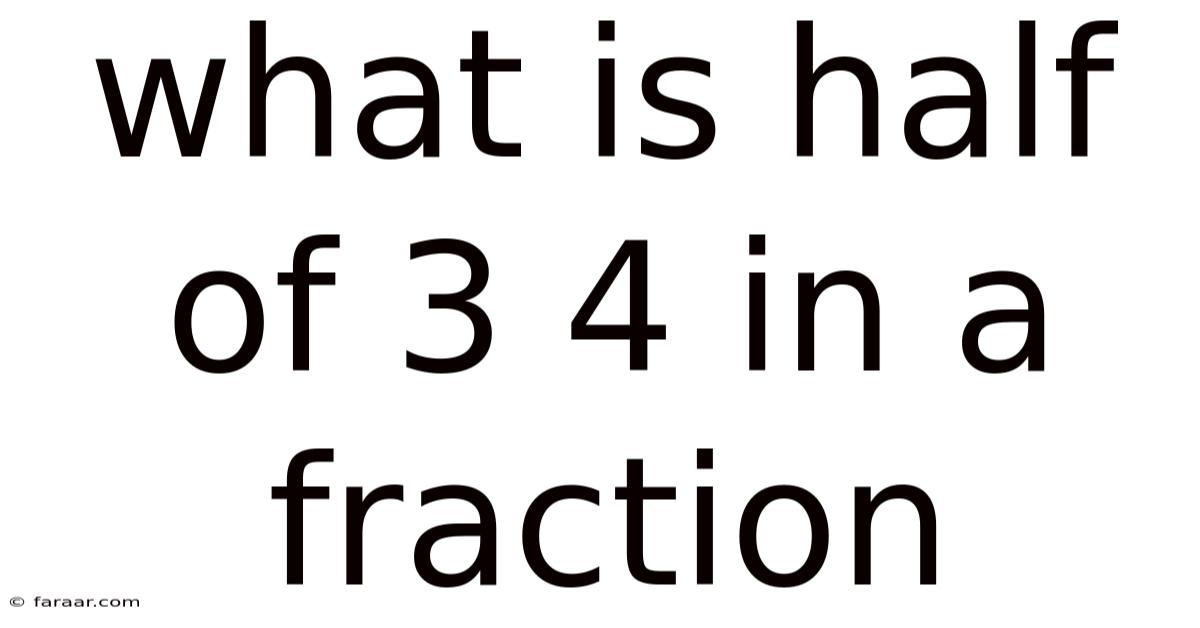
Table of Contents
What is Half of 3/4 in a Fraction? A Deep Dive into Fractions and Division
Finding half of 3/4 might seem like a simple task, but it provides a wonderful opportunity to delve deeper into the world of fractions, solidifying understanding of fundamental mathematical concepts. This article will not only show you how to calculate half of 3/4 but also explain the underlying principles, offering various approaches and exploring related concepts to strengthen your fractional arithmetic skills. We'll cover everything from basic fraction multiplication to more advanced techniques, making sure you grasp the "why" behind the calculations as much as the "how."
Understanding Fractions: A Quick Refresher
Before we jump into finding half of 3/4, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two main parts:
- Numerator: The top number, indicating how many parts you have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator (3) tells us we have three parts, and the denominator (4) tells us the whole is divided into four equal parts.
Method 1: Direct Multiplication
The most straightforward way to find half of 3/4 is to multiply the fraction by 1/2. Remember, "half" is simply another way of saying "one-half" or 1/2. Multiplying fractions involves multiplying the numerators together and the denominators together:
(3/4) * (1/2) = (3 * 1) / (4 * 2) = 3/8
Therefore, half of 3/4 is 3/8.
Method 2: Dividing by 2
Another approach involves dividing the fraction 3/4 by 2. To divide a fraction by a whole number, you can multiply the fraction by the reciprocal of the whole number. The reciprocal of a number is simply 1 divided by that number. The reciprocal of 2 is 1/2. Therefore, dividing 3/4 by 2 is the same as multiplying 3/4 by 1/2:
(3/4) / 2 = (3/4) * (1/2) = 3/8
This again confirms that half of 3/4 is 3/8.
Method 3: Visual Representation
Visualizing fractions can often make abstract concepts easier to understand. Imagine a pizza cut into four equal slices. 3/4 of the pizza represents three of these slices. To find half of 3/4, we would take half of those three slices. This would leave us with 1.5 slices, but since we're working with fractions, we need to maintain the same denominator. If we divide each of the four original slices in half, we now have eight slices. The 1.5 slices from before now represent 3 out of these 8 slices, giving us the fraction 3/8.
Simplifying Fractions
Once you've performed the calculation, it's always good practice to simplify the resulting fraction to its lowest terms. A fraction is in its simplest form when the greatest common divisor (GCD) of the numerator and the denominator is 1. In this case, the fraction 3/8 is already in its simplest form because 3 and 8 have no common divisors other than 1.
Extending the Concept: Finding a Fraction of a Fraction
The process of finding half of 3/4 illustrates a broader concept: finding a fraction of a fraction. This involves multiplying two fractions together. Let's consider a slightly more complex example: finding 2/3 of 3/4.
(2/3) * (3/4) = (2 * 3) / (3 * 4) = 6/12
Notice that the fraction 6/12 can be simplified. Both the numerator (6) and the denominator (12) are divisible by 6:
6/12 = (6/6) / (12/6) = 1/2
Therefore, 2/3 of 3/4 is 1/2.
Understanding the Mathematical Principles
The process of multiplying fractions relies on the distributive property of multiplication. When multiplying fractions, we are essentially finding the area of a rectangle with fractional sides. The length and width of the rectangle are represented by the two fractions, and the area (the product) is the result of multiplying the numerators and denominators.
Practical Applications of Fractions
Understanding fractions is crucial for many aspects of daily life. From cooking (measuring ingredients) to construction (calculating measurements) and even finance (understanding percentages and proportions), the ability to work with fractions is essential.
Frequently Asked Questions (FAQ)
Q: Can I use decimals instead of fractions?
A: You certainly can! 3/4 is equivalent to 0.75. Half of 0.75 is 0.375, which is equivalent to 3/8. While using decimals might be simpler for some calculations, understanding fractions is crucial for a comprehensive understanding of mathematics.
Q: What if I need to find more than half? For example, what is 2/3 of 3/4?
A: You'd use the same principle: multiply the two fractions together. (2/3) * (3/4) = 6/12 = 1/2
Q: Are there other ways to visualize finding half of 3/4?
A: Yes! You could use a number line, dividing the space between 0 and 1 into fourths, then further dividing each fourth in half to represent eighths. Locating 3/4 and then finding the midpoint between 3/4 and 0 would clearly show the result as 3/8.
Conclusion: Mastering Fractions for a Stronger Mathematical Foundation
Finding half of 3/4, while seemingly basic, serves as a gateway to a deeper understanding of fractions, their manipulation, and their practical application. By understanding the methods – direct multiplication, division by the reciprocal, and visual representations – you build a strong foundation in fractional arithmetic. This foundational knowledge is vital for more advanced mathematical concepts and extends to numerous aspects of everyday life. Remember, practice is key! The more you work with fractions, the more intuitive and comfortable you will become. Continue exploring different fraction problems and challenges to further enhance your understanding and master this crucial aspect of mathematics.
Latest Posts
Latest Posts
-
Some Irrational Numbers Are Integers True Or False
Sep 15, 2025
-
What Is Difference Between A Compound And A Mixture
Sep 15, 2025
-
How To Use By Which In A Sentence
Sep 15, 2025
-
Why Is Chemistry Important In The Study Of Biology
Sep 15, 2025
-
Three Basic Parts Of A Nucleotide
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 3 4 In A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.