What Is Half Of 2 1/4
faraar
Sep 14, 2025 · 6 min read
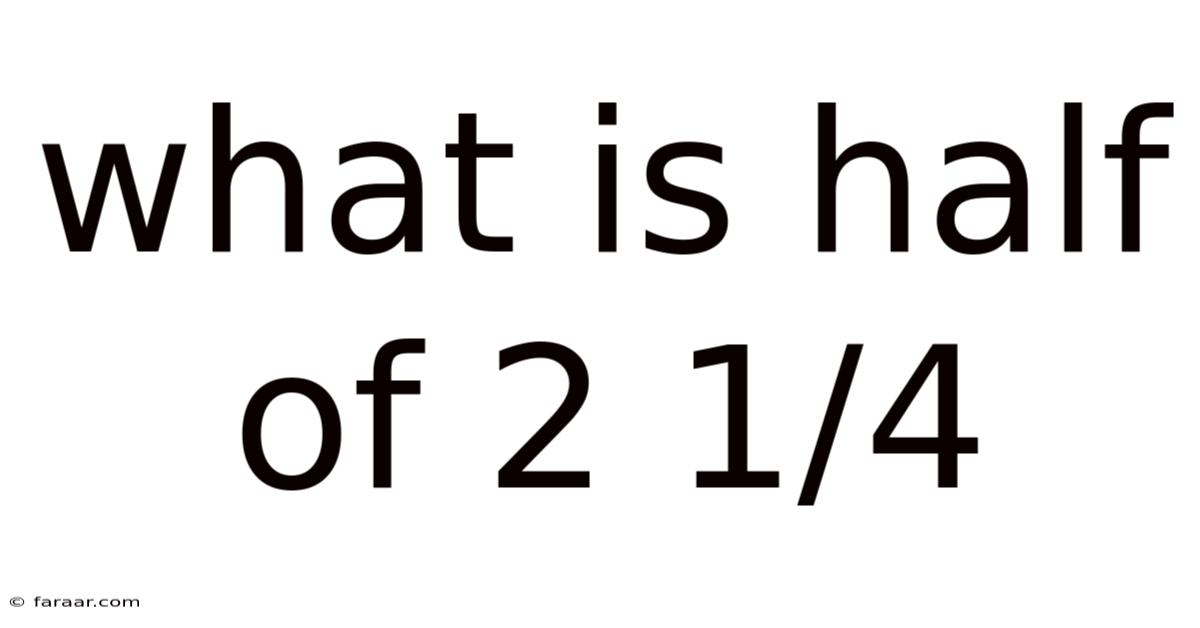
Table of Contents
What is Half of 2 1/4? A Comprehensive Guide to Fraction Division
Finding half of 2 1/4 might seem like a simple arithmetic problem, but it offers a fantastic opportunity to delve into the world of fractions and solidify our understanding of fraction division. This comprehensive guide will not only show you how to solve this specific problem but also equip you with the skills and knowledge to tackle similar fraction calculations with confidence. We'll explore various methods, delve into the underlying mathematical principles, and answer frequently asked questions. This guide is perfect for students, educators, or anyone looking to refresh their understanding of fractions.
Understanding Fractions: A Quick Refresher
Before we jump into calculating half of 2 1/4, let's briefly review the basics of fractions. A fraction represents a part of a whole. It consists of two parts:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/4, the numerator (1) represents one part, and the denominator (4) represents that the whole is divided into four equal parts.
Method 1: Converting to Improper Fractions
This method involves converting the mixed number (2 1/4) into an improper fraction before performing the division. An improper fraction has a numerator larger than or equal to its denominator.
Step 1: Convert the mixed number to an improper fraction.
To convert 2 1/4 to an improper fraction, we multiply the whole number (2) by the denominator (4) and add the numerator (1). This result becomes the new numerator, while the denominator remains the same.
(2 x 4) + 1 = 9
Therefore, 2 1/4 is equal to 9/4.
Step 2: Divide by 2 (finding half).
Finding half of a number is the same as dividing it by 2. To divide a fraction by a whole number, we multiply the fraction by the reciprocal of the whole number. The reciprocal of 2 is 1/2.
(9/4) ÷ 2 = (9/4) x (1/2)
Step 3: Multiply the numerators and denominators.
Multiply the numerators together and the denominators together:
(9 x 1) / (4 x 2) = 9/8
Step 4: Convert back to a mixed number (optional).
The improper fraction 9/8 can be converted back into a mixed number by dividing the numerator (9) by the denominator (8).
9 ÷ 8 = 1 with a remainder of 1
Therefore, 9/8 is equal to 1 1/8.
Conclusion: Half of 2 1/4 is 1 1/8.
Method 2: Dividing the Whole Number and the Fraction Separately
This method involves dividing the whole number part and the fractional part of the mixed number separately, then combining the results.
Step 1: Divide the whole number.
Half of 2 is 2 ÷ 2 = 1
Step 2: Divide the fraction.
Half of 1/4 is (1/4) ÷ 2 = (1/4) x (1/2) = 1/8
Step 3: Combine the results.
Add the results from Step 1 and Step 2:
1 + 1/8 = 1 1/8
Conclusion: Half of 2 1/4 is 1 1/8.
Method 3: Using Decimal Representation
This method involves converting the mixed number into a decimal and then performing the division.
Step 1: Convert the mixed number to a decimal.
2 1/4 can be written as 2.25 (since 1/4 = 0.25).
Step 2: Divide by 2.
2.25 ÷ 2 = 1.125
Step 3: Convert back to a fraction (optional).
1.125 can be written as 1 1/8. We can arrive at this by recognizing that 0.125 is equal to 1/8.
Conclusion: Half of 2 1/4 is 1 1/8.
The Mathematical Principles Behind Fraction Division
The core concept behind dividing fractions is the idea of reciprocals. The reciprocal of a number is simply 1 divided by that number. When dividing by a fraction, we actually multiply by its reciprocal. This is because division is the inverse operation of multiplication.
For example, dividing by 1/2 is the same as multiplying by 2 (the reciprocal of 1/2). This principle is applicable regardless of whether we are dealing with simple fractions, mixed numbers, or even decimals.
Practical Applications: Real-World Examples
Understanding how to find half of a quantity is crucial in many everyday situations. Here are a few examples:
- Cooking: If a recipe calls for 2 1/4 cups of flour, and you want to halve the recipe, you'll need 1 1/8 cups.
- Measurement: If you need to cut a piece of wood that is 2 1/4 feet long in half, each piece will be 1 1/8 feet long.
- Sharing: If you have 2 1/4 pizzas and want to share them equally between two people, each person gets 1 1/8 pizzas.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this?
A: Yes, you can use a calculator to convert the mixed number to a decimal and then divide by 2. However, understanding the methods outlined above will help you solve similar problems even without a calculator.
Q: What if I need to find a different fraction of 2 1/4, such as one-third?
A: The same principles apply. You would convert 2 1/4 to an improper fraction (9/4) and then multiply it by the reciprocal of the fraction you're dividing by (in this case, 1/3). So, one-third of 2 1/4 would be (9/4) x (1/3) = 3/4.
Q: Why are there different methods to solve this problem?
A: Different methods cater to different learning styles and preferences. Some people find the improper fraction method more intuitive, while others might prefer the separate division method. The decimal method is useful for those who are more comfortable working with decimals. Ultimately, the best method is the one that you find easiest to understand and apply consistently.
Q: What if the fraction was more complex?
A: The principles remain the same. Convert mixed numbers to improper fractions, find the reciprocal when dividing, and simplify the resulting fraction. Practice is key to mastering these skills.
Conclusion
Finding half of 2 1/4, resulting in 1 1/8, is a straightforward calculation that highlights the fundamental concepts of fraction manipulation. By understanding the different methods presented—converting to improper fractions, dividing separately, and utilizing decimals—you gain a robust foundation for tackling a wide range of fraction problems. Remember, practice is key to mastering these skills, and the ability to work confidently with fractions is a valuable asset in various aspects of life, from cooking and crafting to more complex mathematical and scientific endeavors. This understanding empowers you to approach more complex fraction problems with clarity and confidence. Remember to choose the method you find most comfortable and practice regularly to build fluency and accuracy.
Latest Posts
Latest Posts
-
2 And 1 4 Divided By 2
Sep 14, 2025
-
How Many Ounces In A Cupcake
Sep 14, 2025
-
Eight Plus The Quotient Of A Number And 3 Is
Sep 14, 2025
-
How To Make Phosphate Buffer Solution
Sep 14, 2025
-
Brian Has Some Boxes Of Paper Clips
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 2 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.