What Is 3 4 Of 1 2
faraar
Sep 13, 2025 · 5 min read
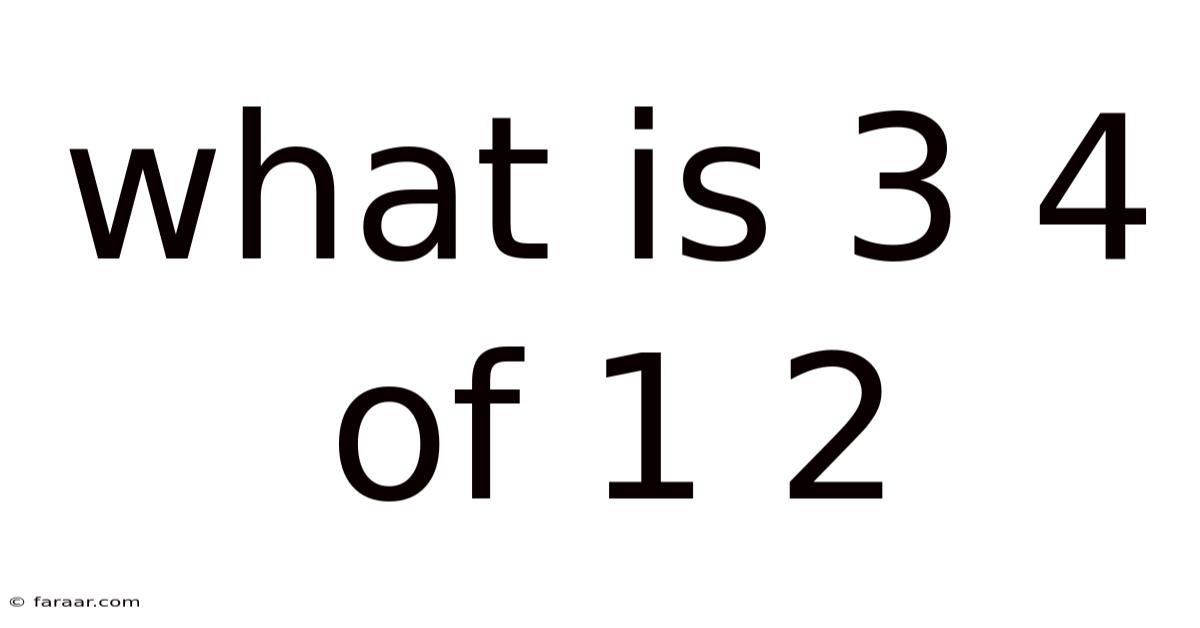
Table of Contents
What is 3/4 of 1/2? A Deep Dive into Fractions and Their Applications
Finding 3/4 of 1/2 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding this calculation unlocks a deeper understanding of fractions, their manipulation, and their widespread applications in various fields. This article will not only provide the answer but also explore the underlying concepts, different methods of solving the problem, and practical examples demonstrating the relevance of fractional calculations in everyday life.
Introduction: Understanding Fractions
Before diving into the calculation, let's refresh our understanding of fractions. A fraction represents a part of a whole. It is expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/2, the numerator (1) represents one part, and the denominator (2) signifies that the whole is divided into two equal parts.
Our problem, "What is 3/4 of 1/2?", essentially asks us to find three-quarters of one-half. This involves multiplying two fractions, a core concept in fractional arithmetic.
Method 1: Direct Multiplication of Fractions
The most straightforward way to solve "What is 3/4 of 1/2?" is by directly multiplying the two fractions. This involves multiplying the numerators together and the denominators together.
- Step 1: Multiply the numerators: 3 x 1 = 3
- Step 2: Multiply the denominators: 4 x 2 = 8
- Step 3: Combine the results: The answer is 3/8
Therefore, 3/4 of 1/2 is 3/8.
Method 2: Visual Representation
Visual aids can significantly enhance understanding, especially when dealing with fractions. Let's visualize this problem:
Imagine a rectangle representing the whole (1). Divide this rectangle in half horizontally (1/2). Now, take one of these halves and divide it into four equal parts vertically (representing quarters of a half). Shading three of these four parts visually demonstrates that 3/4 of 1/2 equals 3 out of 8 equal parts of the original rectangle – confirming our answer of 3/8.
Method 3: Converting to Decimals
Another approach is to convert the fractions into decimals before performing the calculation.
- Step 1: Convert 3/4 to a decimal: 3 ÷ 4 = 0.75
- Step 2: Convert 1/2 to a decimal: 1 ÷ 2 = 0.5
- Step 3: Multiply the decimals: 0.75 x 0.5 = 0.375
- Step 4: Convert the decimal back to a fraction (optional): 0.375 can be converted back to a fraction by placing the decimal over a power of 10 and simplifying: 375/1000 which simplifies to 3/8.
This method provides an alternative pathway to arrive at the same answer: 3/8.
Explanation of the Calculation: A Deeper Dive
The multiplication of fractions is fundamentally about finding a portion of a portion. When we say "3/4 of 1/2," we're taking three-quarters of the quantity represented by one-half. The multiplication process reflects this sequential action of taking a fraction of another fraction.
The result, 3/8, signifies that we have three parts out of eight equal parts of the original whole. This fraction can't be further simplified, meaning it is in its simplest form.
Practical Applications of Fractional Calculations
Fractional calculations are not limited to mathematical exercises; they have practical applications in numerous real-world scenarios:
- Cooking and Baking: Recipes often involve fractions (e.g., 1/2 cup of sugar, 3/4 teaspoon of salt). Accurate fractional calculations are crucial for achieving desired results.
- Construction and Engineering: Accurate measurements and calculations using fractions are essential in construction projects, ensuring precise dimensions and structural integrity.
- Finance and Budgeting: Understanding fractions helps in managing finances, calculating percentages (which are essentially fractions), and determining proportions of income and expenses.
- Data Analysis: In statistics and data analysis, fractions are used extensively to represent proportions, probabilities, and ratios within datasets.
- Science and Medicine: Fractional calculations are vital in scientific experiments, measuring quantities, and analyzing data, as well as in calculating dosages in medicine.
Frequently Asked Questions (FAQs)
-
Q: Can I add or subtract fractions directly to find 3/4 of 1/2?
- A: No, adding or subtracting fractions requires a common denominator. Multiplication of fractions directly finds the desired portion.
-
Q: What if the fractions were more complex?
- A: The same principle applies. Multiply the numerators and denominators, then simplify the resulting fraction.
-
Q: Is there a shortcut for multiplying fractions?
- A: Sometimes, you can simplify before multiplying by canceling common factors between the numerator and denominator. For example, in the problem 1/2 x 2/3, the 2 in the numerator and denominator can cancel each other, leaving 1/3. However, this wasn't necessary in our problem.
-
Q: Why is understanding fractions important?
- A: Fractions are fundamental to mathematics and have numerous real-world applications, making them crucial for problem-solving and understanding various concepts in various fields.
Conclusion: Mastering the Fundamentals
The seemingly simple problem of finding "What is 3/4 of 1/2?" serves as a gateway to a deeper comprehension of fractional arithmetic. Understanding the process of multiplying fractions, visualizing the concept, and exploring various calculation methods builds a strong foundation for tackling more complex mathematical problems. The applications of fractional calculations extend far beyond the classroom, impacting various aspects of our daily lives and demonstrating their inherent importance in navigating the world around us. Remember, mastering the fundamentals of fractions provides a powerful toolset for tackling a wide range of challenges. So, next time you encounter a fraction problem, remember the steps and the practical relevance of the concepts involved. You'll find that understanding fractions unlocks a deeper understanding of the world around you.
Latest Posts
Latest Posts
-
How To Find The Inverse Of Square Root Function
Sep 13, 2025
-
3 Words To Describe Macbeths State Of Mind
Sep 13, 2025
-
How To Find Length And Width With Area
Sep 13, 2025
-
How To Find Net Change Between Two Points
Sep 13, 2025
-
Is Square Root Of 13 A Rational Number
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 4 Of 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.