What Is 3/4 Divided By 1/4
faraar
Sep 04, 2025 · 6 min read
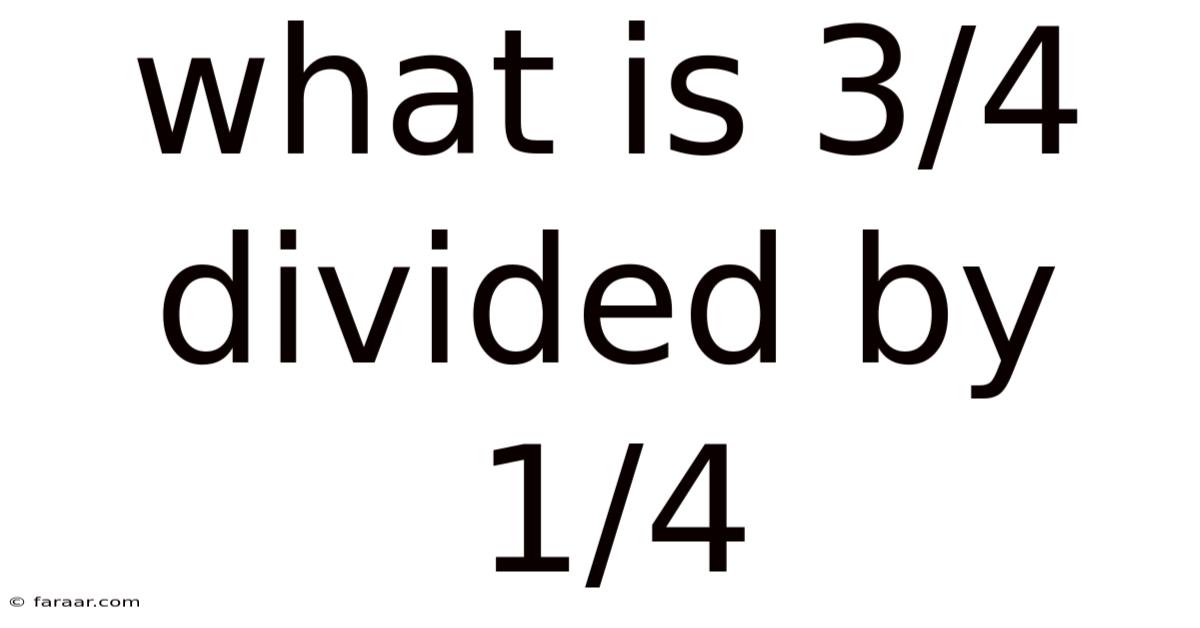
Table of Contents
What is 3/4 Divided by 1/4? A Comprehensive Guide to Fraction Division
Understanding fraction division can seem daunting at first, but with a clear explanation and a few helpful strategies, it becomes surprisingly straightforward. This comprehensive guide will not only show you how to solve 3/4 divided by 1/4 but also equip you with the knowledge to tackle any fraction division problem with confidence. We'll explore the underlying principles, delve into different methods, and address common questions, ensuring a complete understanding of this fundamental mathematical concept.
Introduction: Understanding Fraction Division
Dividing fractions might seem different from dividing whole numbers, but the core concept remains the same: finding out how many times one quantity fits into another. When we divide 3/4 by 1/4, we're essentially asking, "How many times does 1/4 fit into 3/4?" This seemingly simple question opens the door to a deeper understanding of fractions and their manipulation. The problem, 3/4 ÷ 1/4, is asking us to determine how many groups of 1/4 are present within 3/4.
The answer, as we'll see shortly, is 3. But the journey to arrive at this answer will provide a solid foundation for tackling more complex fraction division problems.
Method 1: The "Keep, Change, Flip" Method (Invert and Multiply)
This is arguably the most popular and easiest method for dividing fractions. It involves three simple steps:
- Keep the first fraction (the dividend) exactly as it is.
- Change the division sign (÷) to a multiplication sign (×).
- Flip the second fraction (the divisor) – this means inverting the numerator and the denominator.
Let's apply this to our problem:
3/4 ÷ 1/4
- Keep: 3/4
- Change: ÷ becomes ×
- Flip: 1/4 becomes 4/1
Now, our problem becomes:
3/4 × 4/1
Multiply the numerators together (3 × 4 = 12) and the denominators together (4 × 1 = 4):
12/4
Finally, simplify the resulting fraction:
12/4 = 3
Therefore, 3/4 divided by 1/4 equals 3.
Method 2: Visual Representation using Models
A visual approach can greatly enhance understanding, particularly for those who prefer a more intuitive method. Imagine a pizza cut into four equal slices. 3/4 represents three of these slices. 1/4 represents one slice. How many times does one slice (1/4) fit into three slices (3/4)? The answer, visually evident, is three. This method provides a concrete representation of the abstract concept of fraction division. This visualization technique works best with simpler fractions but helps to build an intuitive understanding that can be applied to more complex scenarios.
Method 3: Finding a Common Denominator
This method is less direct but provides a deeper insight into the underlying principles of fraction division. It involves finding a common denominator for both fractions and then dividing the numerators.
-
Find a common denominator: In this case, the common denominator for 3/4 and 1/4 is already 4.
-
Rewrite the fractions: The fractions remain the same: 3/4 and 1/4.
-
Divide the numerators: Now, divide the numerator of the first fraction (3) by the numerator of the second fraction (1): 3 ÷ 1 = 3.
This method confirms our earlier findings: 3/4 divided by 1/4 equals 3. While this method might seem less efficient for this specific problem, it illustrates a foundational principle applicable to a wider range of fraction division problems, especially those with different denominators.
The Mathematical Explanation: Reciprocal and Multiplication
The "keep, change, flip" method isn't just a trick; it's based on the concept of reciprocals. The reciprocal of a fraction is obtained by swapping the numerator and the denominator. Dividing by a fraction is equivalent to multiplying by its reciprocal. This is because division is the inverse operation of multiplication. When we "flip" the second fraction, we are essentially multiplying by its reciprocal, which is a fundamental principle in algebra.
Mathematically, we can represent this as follows:
(a/b) ÷ (c/d) = (a/b) × (d/c) = (a × d) / (b × c)
In our problem, a = 3, b = 4, c = 1, and d = 4. Substituting these values, we get:
(3/4) ÷ (1/4) = (3/4) × (4/1) = (3 × 4) / (4 × 1) = 12/4 = 3
Extending the Concept: Dividing Fractions with Different Denominators
Let's explore a slightly more complex scenario to solidify our understanding. What is 2/3 divided by 1/6?
Using the "keep, change, flip" method:
2/3 ÷ 1/6 = 2/3 × 6/1 = 12/3 = 4
Alternatively, using the common denominator method:
Find the common denominator for 2/3 and 1/6 (which is 6). Rewrite the fractions: 4/6 and 1/6. Divide the numerators: 4 ÷ 1 = 4.
Both methods yield the same result: 2/3 divided by 1/6 equals 4. This demonstrates the versatility and reliability of these techniques in handling various fraction division problems.
Frequently Asked Questions (FAQ)
Q: Why does the "keep, change, flip" method work?
A: The method works because dividing by a fraction is equivalent to multiplying by its reciprocal. Flipping the fraction is simply finding its reciprocal.
Q: Can I use a calculator to divide fractions?
A: Yes, most calculators can handle fraction division. However, understanding the underlying principles is crucial for problem-solving and developing a strong mathematical foundation.
Q: What if the resulting fraction is an improper fraction (numerator larger than denominator)?
A: Convert the improper fraction to a mixed number (a whole number and a fraction) to represent the answer more clearly. For instance, 12/4 becomes 3.
Q: What if I have mixed numbers (a whole number and a fraction)?
A: Convert the mixed numbers into improper fractions before applying any of the division methods. For example, 1 1/2 becomes 3/2.
Conclusion: Mastering Fraction Division
Fraction division, initially perceived as complex, becomes manageable with the right approach. This guide has presented three methods – the "keep, change, flip" method, the visual representation method, and the common denominator method – all leading to the same accurate result. Understanding these methods and the underlying mathematical principles empowers you to confidently tackle any fraction division problem. Remember to practice regularly to build fluency and solidify your understanding. The more you practice, the more intuitive and effortless fraction division will become, paving the way for more advanced mathematical concepts. The key is to choose the method that you find most comfortable and effective for you, and remember that the core principle is always the same: understanding how many times one fraction fits into another.
Latest Posts
Latest Posts
-
For The Polynomial Below 2 Is A Zero
Sep 06, 2025
-
Ap Calculus Bc Tutor Near Me
Sep 06, 2025
-
Have You Or A Loved One
Sep 06, 2025
-
A Cat Walks In A Straight Line
Sep 06, 2025
-
Which Equation Is Equivalent To 2 4x 8 X 3
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/4 Divided By 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.