What Is 3 2 Equal To
faraar
Sep 15, 2025 · 5 min read
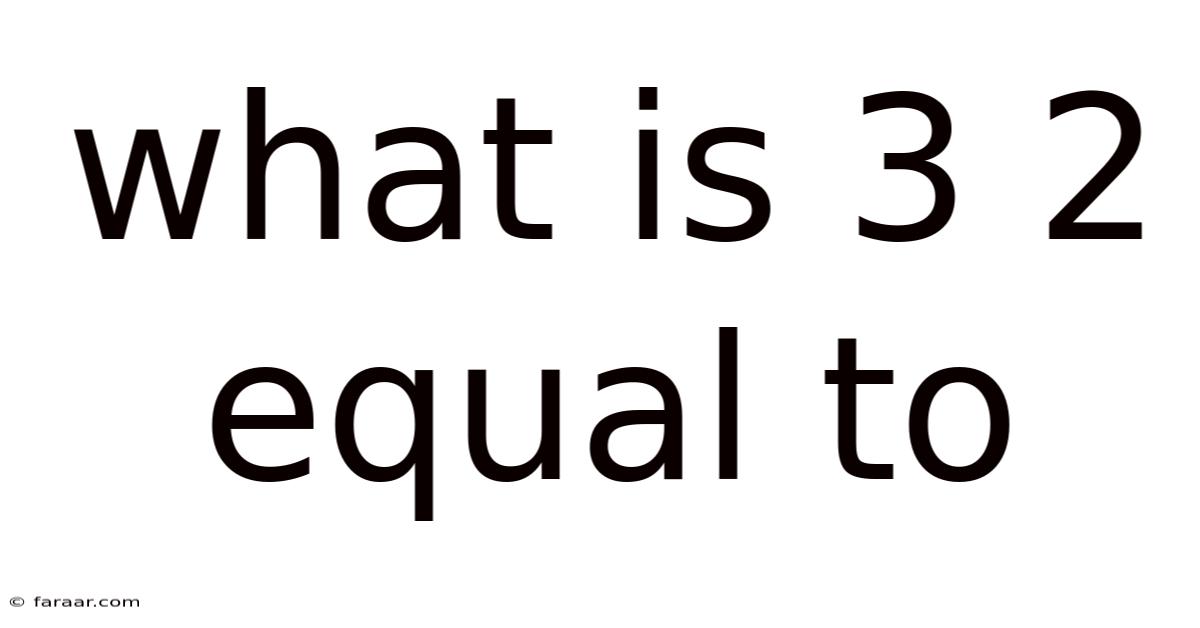
Table of Contents
What is 3² Equal To? Understanding Exponents and Their Applications
The question "What is 3² equal to?" might seem deceptively simple, especially to those familiar with basic math. However, understanding this seemingly straightforward calculation unlocks a deeper comprehension of exponents, their fundamental properties, and their widespread applications across various fields, from simple arithmetic to advanced calculus and computer science. This article will delve into the meaning of 3², explore the broader concept of exponents, and illustrate their importance through real-world examples.
Understanding Exponents: The Power of Repeated Multiplication
The expression 3² represents an exponent, also known as a power or index. It signifies repeated multiplication. In this specific case, the base is 3, and the exponent is 2. This means we multiply the base (3) by itself the number of times indicated by the exponent (2). Therefore, 3² is equivalent to 3 multiplied by 3, which equals 9.
3² = 3 x 3 = 9
This simple example lays the foundation for understanding more complex exponential expressions. Let's explore the general form of an exponent:
bⁿ
Where:
- b represents the base – the number being multiplied.
- n represents the exponent – the number of times the base is multiplied by itself.
For instance:
- 5³ = 5 x 5 x 5 = 125
- 2⁴ = 2 x 2 x 2 x 2 = 16
- 10¹ = 10 (Any number raised to the power of 1 is itself)
- 7⁰ = 1 (Any non-zero number raised to the power of 0 is 1)
Beyond the Basics: Exploring Different Exponents
Understanding exponents involves more than just positive integers. Let's look at other types of exponents:
-
Negative Exponents: A negative exponent indicates the reciprocal of the base raised to the positive exponent. For example:
- 3⁻² = 1/3² = 1/(3 x 3) = 1/9
-
Fractional Exponents: Fractional exponents are closely related to roots. For example:
- 9^(1/2) = √9 = 3 (The square root of 9)
- 8^(1/3) = ³√8 = 2 (The cube root of 8)
- 16^(3/4) = (16^(1/4))³ = (2)³ = 8
-
Zero Exponent: As mentioned earlier, any non-zero number raised to the power of zero is equal to 1. This is a fundamental rule in exponent mathematics.
-
Decimal Exponents: Decimal exponents can be handled by converting them into fractions. For instance, 2⁵•² could be expressed as 2⁵²/¹⁰, which can then be calculated using the rules of fractional exponents and logarithms.
The Laws of Exponents: Simplifying Complex Expressions
Working with exponents often involves manipulating multiple terms. The laws of exponents provide rules for simplifying these complex expressions. These laws are crucial for algebraic manipulation and solving various mathematical problems. Here are some key laws:
-
Product of Powers: When multiplying two terms with the same base, add the exponents: bᵐ x bⁿ = b^(m+n)
-
Quotient of Powers: When dividing two terms with the same base, subtract the exponents: bᵐ / bⁿ = b^(m-n)
-
Power of a Power: When raising a power to another power, multiply the exponents: (bᵐ)ⁿ = b^(m x n)
-
Power of a Product: When raising a product to a power, raise each factor to that power: (ab)ⁿ = aⁿbⁿ
-
Power of a Quotient: When raising a quotient to a power, raise both the numerator and denominator to that power: (a/b)ⁿ = aⁿ/bⁿ
Real-World Applications of Exponents: From Finance to Physics
Exponents are not merely abstract mathematical concepts; they have far-reaching applications in various fields. Here are some examples:
-
Compound Interest: The formula for compound interest uses exponents to calculate the future value of an investment. The formula is A = P(1 + r/n)^(nt), where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
-
Population Growth: Exponential functions are used to model population growth (both human and animal populations), where the growth rate is proportional to the current population size.
-
Radioactive Decay: Radioactive decay follows an exponential decay model, which describes the decrease in the amount of a radioactive substance over time. The half-life of a radioactive substance is a key concept in this model.
-
Computer Science: Exponents are fundamental in computer science, particularly in algorithms and data structures. Big O notation, which describes the efficiency of algorithms, often uses exponential functions to represent the time or space complexity of an algorithm.
-
Physics: Many physical phenomena, such as the intensity of light, sound waves, and earthquake magnitudes, are described using logarithmic scales, which are intimately connected to exponents.
Solving Equations with Exponents
Understanding exponents is crucial for solving various types of equations. For example, consider the equation:
2ˣ = 16
To solve for x, we need to express 16 as a power of 2:
2ˣ = 2⁴
Since the bases are the same, we can equate the exponents:
x = 4
More complex exponential equations might involve logarithms to solve for the unknown variable.
Frequently Asked Questions (FAQ)
Q: What is the difference between 3² and 2³?
A: 3² (3 squared) means 3 x 3 = 9. 2³ (2 cubed) means 2 x 2 x 2 = 8. The base and exponent are different, resulting in different outcomes.
Q: Can exponents be negative numbers?
A: Yes, negative exponents represent reciprocals. For example, 3⁻² = 1/3² = 1/9.
Q: What is an exponent of 0?
A: Any non-zero number raised to the power of 0 is equal to 1. This is a fundamental rule in exponential mathematics.
Q: How do I calculate expressions with both multiplication and exponents?
A: Follow the order of operations (PEMDAS/BODMAS): Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
Conclusion: Mastering Exponents – A Foundation for Further Learning
Understanding the concept of "What is 3² equal to?" is not just about arriving at the answer 9. It's about grasping a fundamental mathematical concept with wide-ranging applications. From simple calculations to complex scientific models, exponents form a crucial building block in mathematics and its numerous applications in science, technology, engineering, and finance. By mastering the basic principles and the laws of exponents, you open doors to a deeper understanding of mathematics and its power to describe and model the world around us. Continue exploring different exponent types and practicing the laws of exponents to solidify your understanding and build a strong foundation for future mathematical studies.
Latest Posts
Latest Posts
-
Half Of 5 1 2 Inches
Sep 15, 2025
-
How To Shut Up In Spanish
Sep 15, 2025
-
How Do You Calculate The Mass Of Water
Sep 15, 2025
-
A 9y 3yx Solve For Y
Sep 15, 2025
-
Use Synthetic Division To Find The Quotient And The Remainder
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 2 Equal To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.