What Is 2 3 Of 3 Quarts
faraar
Aug 28, 2025 · 6 min read
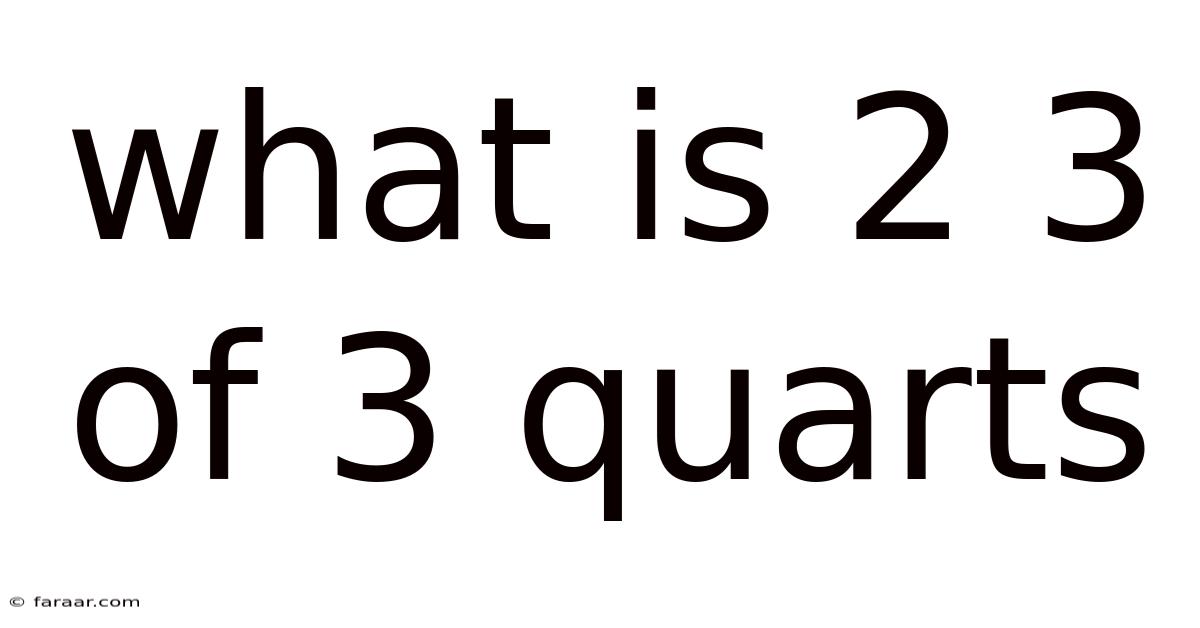
Table of Contents
What is 2/3 of 3 Quarts? A Deep Dive into Fractions and Measurement
Understanding fractions and their application in everyday measurements is a fundamental skill. This article will thoroughly explore the question, "What is 2/3 of 3 quarts?", breaking down the calculation step-by-step and expanding on the underlying concepts of fractions, unit conversion, and practical applications in various fields. We'll cover the mathematical process, provide real-world examples, and address frequently asked questions to ensure a complete understanding of this seemingly simple yet crucial topic.
Understanding Fractions: A Quick Refresher
Before diving into the calculation, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator shows the total number of equal parts the whole is divided into. For example, in the fraction 2/3, 2 is the numerator and 3 is the denominator. This means we have 2 out of 3 equal parts.
Calculating 2/3 of 3 Quarts: The Step-by-Step Approach
To find 2/3 of 3 quarts, we need to perform a simple multiplication:
(2/3) x 3 quarts
There are two ways to approach this calculation:
Method 1: Direct Multiplication
This method involves directly multiplying the fraction by the whole number:
(2/3) x 3 = (2 x 3) / 3 = 6 / 3 = 2
Therefore, 2/3 of 3 quarts is 2 quarts.
Method 2: Understanding the Concept of "of"
The word "of" in mathematics often implies multiplication. Thinking about it conceptually, we can break down the problem as follows:
- We have 3 quarts, which is our whole.
- We want to find 2/3 of this whole.
- To find one-third (1/3) of 3 quarts, we divide 3 quarts by 3: 3 quarts / 3 = 1 quart.
- Since we want two-thirds (2/3), we multiply the result by 2: 1 quart x 2 = 2 quarts.
Again, we arrive at the answer: 2/3 of 3 quarts is 2 quarts.
Expanding the Concept: Working with Different Fractions and Units
The method used above applies to various fractions and units of measurement. Let's explore some examples:
- Finding 1/4 of 8 liters: (1/4) x 8 liters = 2 liters
- Finding 3/5 of 10 kilograms: (3/5) x 10 kilograms = 6 kilograms
- Finding 2/7 of 14 meters: (2/7) x 14 meters = 4 meters
These examples highlight the versatility of the concept. The core principle remains the same: multiply the fraction by the quantity to find the desired portion.
Real-World Applications: From Cooking to Construction
Understanding fractions and their application in measurement is crucial in various real-world scenarios:
-
Cooking and Baking: Recipes often require specific fractional amounts of ingredients. Knowing how to calculate fractions accurately ensures the recipe's success. For example, a recipe might call for 2/3 cup of sugar, and understanding this calculation ensures you use the right amount.
-
Construction and Engineering: Accurate measurements are essential in construction and engineering. Fractions are frequently used in blueprints, calculations for material quantities, and ensuring precise dimensions for structural elements. Incorrect calculations can lead to significant errors and potentially safety hazards.
-
Finance and Business: Fractions play a vital role in financial calculations, such as determining percentages, calculating interest rates, or analyzing financial ratios. Accurate fractional calculations are critical for sound financial decisions.
-
Science and Research: In many scientific fields, precise measurements are fundamental. Fractions are used extensively in data analysis, experiments, and research involving various units of measurement.
-
Everyday Life: Even in everyday situations, understanding fractions can be beneficial. For instance, dividing a pizza equally among friends or sharing a collection of items fairly requires an understanding of fractional parts.
Dealing with More Complex Scenarios: Mixed Numbers and Improper Fractions
While the example we worked with was straightforward, let's consider more complex scenarios involving mixed numbers and improper fractions.
Mixed Numbers: A mixed number combines a whole number and a fraction (e.g., 1 1/2). To calculate with mixed numbers, it's often easier to convert them into improper fractions. An improper fraction has a numerator larger than its denominator (e.g., 3/2).
Example: Let's find 2/3 of 1 1/2 quarts.
-
Convert the mixed number to an improper fraction: 1 1/2 = (1 x 2 + 1) / 2 = 3/2 quarts
-
Multiply the fractions: (2/3) x (3/2) quarts = 6/6 quarts = 1 quart
Therefore, 2/3 of 1 1/2 quarts is 1 quart.
Improper Fractions: Calculations with improper fractions follow the same principle as with proper fractions.
Example: Let's find 5/4 of 8 quarts.
(5/4) x 8 quarts = 40/4 quarts = 10 quarts
Unit Conversion: Expanding the Scope of Understanding
The ability to convert units is equally important. Let's consider the same problem but with a different unit:
What is 2/3 of 3 quarts expressed in pints?
-
Calculate 2/3 of 3 quarts: As we've established, this equals 2 quarts.
-
Convert quarts to pints: There are 2 pints in 1 quart.
-
Perform the conversion: 2 quarts x 2 pints/quart = 4 pints
Therefore, 2/3 of 3 quarts is equivalent to 4 pints.
Frequently Asked Questions (FAQ)
Q1: What if the number isn't divisible by the denominator?
A1: If the whole number isn't divisible by the denominator, you'll still perform the multiplication. The result might be an improper fraction, which you can then simplify or convert to a mixed number. For example: 2/5 of 7 liters = 14/5 liters, which simplifies to 2 4/5 liters.
Q2: Can I use a calculator for these calculations?
A2: Yes, absolutely! Calculators are helpful for more complex calculations involving larger numbers or more intricate fractions. However, understanding the underlying principles is crucial for problem-solving and ensuring accuracy.
Q3: Are there any online tools or resources to help with fraction calculations?
A3: Many online resources and calculators are available to assist with fraction calculations. These tools can be valuable for checking your work or tackling more complex problems. However, always strive to understand the fundamental concepts before relying solely on technology.
Conclusion: Mastering Fractions – A Gateway to Deeper Understanding
Mastering fractions and applying them to real-world measurements is a fundamental skill with far-reaching implications. Understanding the principles of fraction calculation and unit conversion is not just about solving mathematical problems; it's about developing critical thinking skills applicable to various aspects of life. From baking a perfect cake to designing a sturdy bridge, the ability to accurately calculate fractions and apply unit conversions lays the foundation for success in numerous fields. This article provided a comprehensive guide to understanding and solving problems related to fractions and measurements, equipping you with the knowledge and confidence to tackle similar challenges with ease. Remember to always break down the problem into smaller, manageable steps, and don't hesitate to use different methods to arrive at the solution. The most important element is a solid grasp of the fundamental concepts—the rest will follow.
Latest Posts
Latest Posts
-
A Negative Divided By A Positive Is A
Aug 29, 2025
-
Finding The Equation Of A Secant Line
Aug 29, 2025
-
What Happens When You Divide A Negative By A Positive
Aug 29, 2025
-
Complete The Sentences To Summarize The Article
Aug 29, 2025
-
Which Of The Following Is A Buffer System
Aug 29, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 3 Of 3 Quarts . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.