What Is 2/3 - 1/5 In Fraction Form
faraar
Sep 02, 2025 · 6 min read
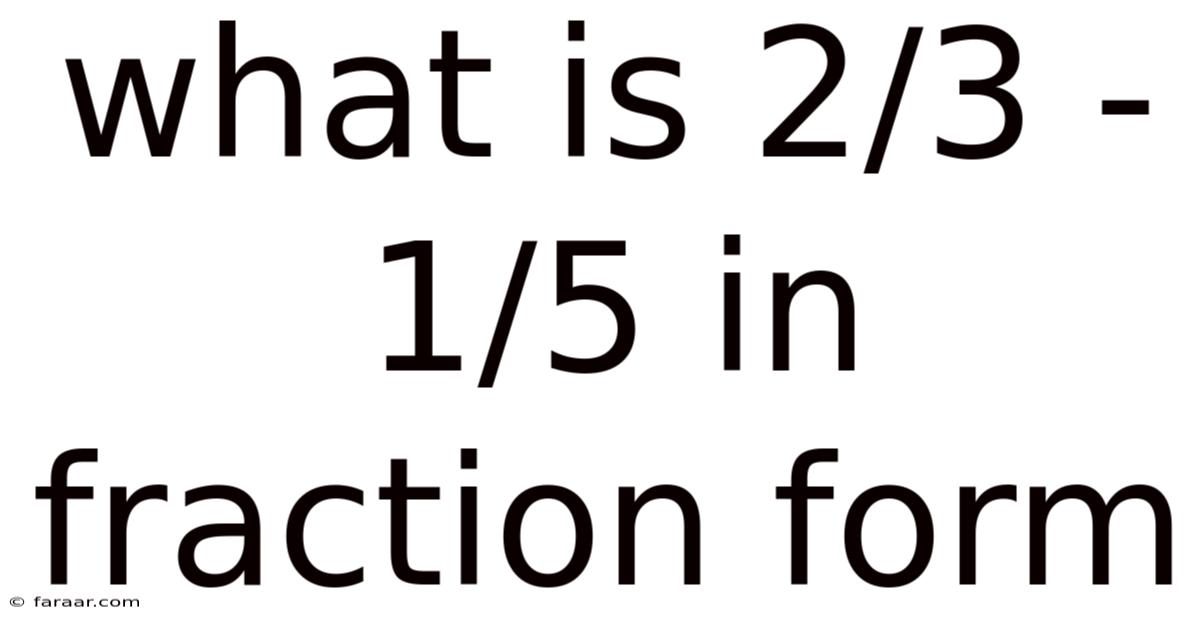
Table of Contents
What is 2/3 - 1/5 in Fraction Form? A Comprehensive Guide to Subtraction of Fractions
This article provides a step-by-step guide on how to subtract the fractions 2/3 and 1/5, explaining the process in detail and exploring the underlying mathematical concepts. Understanding fraction subtraction is crucial for various mathematical applications, from basic arithmetic to advanced calculus. This guide is designed for learners of all levels, from those just beginning to grasp fraction concepts to those looking to solidify their understanding. We'll cover the core method, common mistakes to avoid, and delve into the "why" behind the process, ensuring a comprehensive understanding.
Introduction: Understanding Fractions
Before diving into the subtraction, let's quickly review what fractions are. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 2/3, 2 is the numerator and 3 is the denominator. This means we have 2 out of 3 equal parts of a whole.
Step-by-Step Subtraction of 2/3 - 1/5
Subtracting fractions isn't as straightforward as subtracting whole numbers. We can't directly subtract 1/5 from 2/3 because they have different denominators. This is like trying to compare apples and oranges – they need to be in the same units. To subtract fractions with unlike denominators, we need to find a common denominator.
Step 1: Find the Least Common Denominator (LCD)
The least common denominator is the smallest number that is a multiple of both denominators (3 and 5 in our case). One method to find the LCD is to list the multiples of each denominator:
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21…
- Multiples of 5: 5, 10, 15, 20, 25…
The smallest number that appears in both lists is 15. Therefore, the LCD of 3 and 5 is 15. Alternatively, you can use the method of finding the prime factorization of each denominator and then multiplying the highest powers of each prime factor. For 3, the prime factorization is simply 3. For 5, the prime factorization is 5. Multiplying these together gives us 3 x 5 = 15.
Step 2: Convert Fractions to Equivalent Fractions with the LCD
Now that we have the LCD (15), we need to convert both fractions (2/3 and 1/5) into equivalent fractions with a denominator of 15. To do this, we multiply both the numerator and the denominator of each fraction by the same number so that the denominator becomes 15.
-
For 2/3: To get a denominator of 15, we need to multiply 3 by 5. Therefore, we multiply both the numerator and denominator by 5: (2 x 5) / (3 x 5) = 10/15
-
For 1/5: To get a denominator of 15, we need to multiply 5 by 3. Therefore, we multiply both the numerator and denominator by 3: (1 x 3) / (5 x 3) = 3/15
Step 3: Subtract the Numerators
Now that both fractions have the same denominator, we can subtract them by subtracting their numerators:
10/15 - 3/15 = (10 - 3) / 15 = 7/15
Therefore, 2/3 - 1/5 = 7/15
Understanding the Process: Why it Works
The key to understanding fraction subtraction lies in the concept of equivalent fractions. An equivalent fraction has the same value as the original fraction, but it's represented differently. Multiplying both the numerator and the denominator of a fraction by the same number (except zero) doesn't change its value. This is because you are essentially multiplying the fraction by 1 (e.g., 5/5 = 1).
By converting the fractions to have a common denominator, we are essentially expressing both fractions in the same "units," allowing for direct subtraction. Think of it like converting inches to feet – you can't directly subtract inches from feet unless you convert them to the same unit.
Common Mistakes to Avoid
- Forgetting to find the LCD: This is the most common error. You can't subtract fractions with different denominators directly. Always find the least common denominator before proceeding.
- Incorrectly converting fractions: Remember to multiply both the numerator and the denominator by the same number when creating equivalent fractions.
- Subtracting denominators: The denominators remain the same after subtraction. You only subtract the numerators.
- Not simplifying the result: Always simplify the resulting fraction to its lowest terms. In this case, 7/15 is already in its simplest form because 7 and 15 have no common factors other than 1.
Advanced Considerations: Improper Fractions and Mixed Numbers
Sometimes, you might encounter improper fractions (where the numerator is larger than the denominator) or mixed numbers (a combination of a whole number and a fraction). The process is slightly more involved but follows the same fundamental principles.
Let's consider an example with an improper fraction: 5/2 - 3/4
-
Find the LCD: The LCD of 2 and 4 is 4.
-
Convert to equivalent fractions: 5/2 becomes 10/4 (multiplying both numerator and denominator by 2).
-
Subtract: 10/4 - 3/4 = 7/4. This is an improper fraction.
-
Convert to a mixed number (optional): 7/4 can be converted to the mixed number 1 3/4 (7 divided by 4 is 1 with a remainder of 3).
Similarly, if you have mixed numbers, you'll first need to convert them into improper fractions before following the steps outlined above. For example, 2 1/3 - 1 1/2 would first be converted to 7/3 - 3/2, and then the subtraction process would follow.
Frequently Asked Questions (FAQ)
-
Q: What if the denominators are the same? A: If the denominators are already the same, you can simply subtract the numerators and keep the denominator the same. For example, 5/8 - 3/8 = 2/8 = 1/4 (simplified).
-
Q: Can I use a calculator to solve fraction problems? A: While calculators can help, it's essential to understand the underlying process. Using a calculator without understanding the method can hinder your ability to solve more complex problems.
-
Q: What if I get a negative result? A: If the result is negative, it simply means the second fraction was larger than the first. The same principles apply; just ensure you handle the negative sign correctly.
-
Q: Are there other methods for finding the LCD? A: Yes, the prime factorization method is a more efficient way to find the LCD for larger numbers or fractions with multiple denominators.
Conclusion: Mastering Fraction Subtraction
Subtracting fractions might seem challenging initially, but with practice and a clear understanding of the underlying concepts – especially the importance of finding a common denominator and working with equivalent fractions – it becomes much easier. This article provided a comprehensive guide, walking you through the steps, explaining the rationale, highlighting common mistakes, and extending the concepts to more complex scenarios. Remember, consistent practice is key to mastering any mathematical skill, so don't hesitate to work through additional examples to reinforce your understanding. With dedicated effort, you'll confidently tackle fraction subtraction in any context.
Latest Posts
Latest Posts
-
How To Say Where In German
Sep 02, 2025
-
How Do You Find The Length Of A Trapezoid
Sep 02, 2025
-
What Is The Measure Of Angle Wxy
Sep 02, 2025
-
The Percent Yield Of P4o10 When 6 20 G Of Phosphorus
Sep 02, 2025
-
Given The Equation Which Equation Is Solved For T
Sep 02, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 - 1/5 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.