What Is 15 Percent As A Fraction
faraar
Aug 28, 2025 · 5 min read
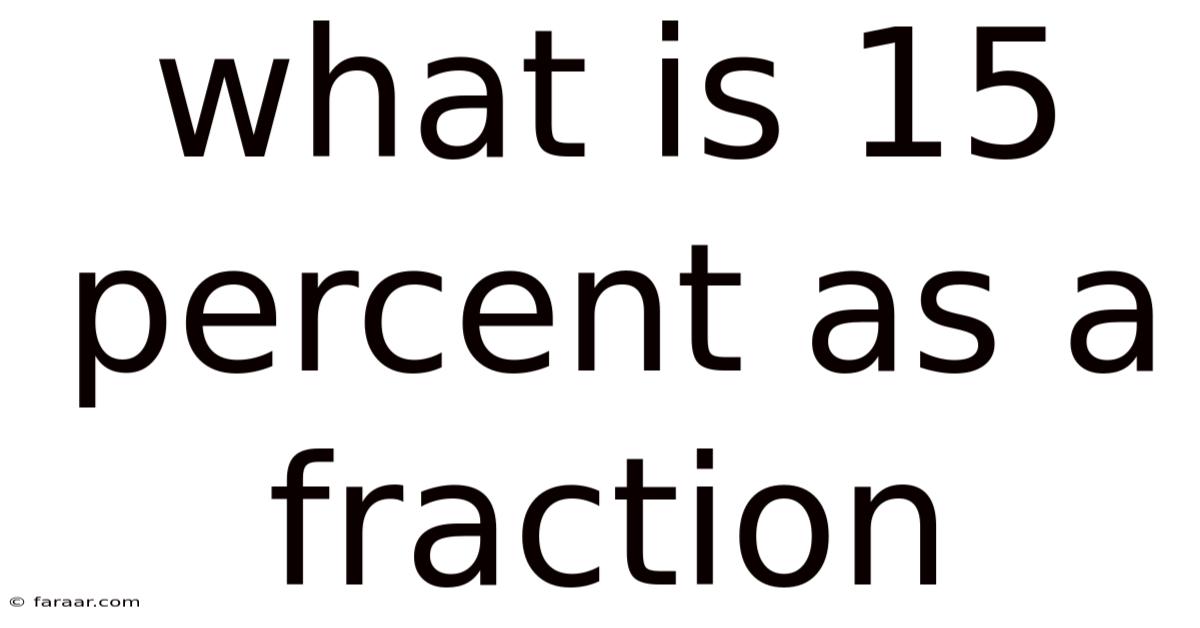
Table of Contents
What is 15 Percent as a Fraction? A Comprehensive Guide
Understanding percentages is a fundamental skill in mathematics with applications spanning various fields, from finance and cooking to science and data analysis. This article will delve deep into converting percentages to fractions, specifically focusing on what is 15 percent as a fraction, and explore related concepts to enhance your understanding. We'll move beyond a simple answer to provide a thorough explanation, covering different methods, practical examples, and frequently asked questions. This comprehensive guide aims to solidify your grasp of percentage-to-fraction conversions and empower you to tackle similar problems with confidence.
Understanding Percentages and Fractions
Before diving into the specifics of 15%, let's establish a solid foundation. A percentage represents a fraction of 100. The word "percent" itself is derived from the Latin "per centum," meaning "out of one hundred." Therefore, 15% literally means 15 out of 100.
A fraction, on the other hand, expresses a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The denominator indicates the total number of parts, and the numerator shows how many of those parts are being considered. For instance, 1/2 represents one out of two equal parts, or one-half.
Converting 15% to a Fraction: The Step-by-Step Approach
Converting 15% to a fraction involves a straightforward process:
-
Write the percentage as a fraction with a denominator of 100: 15% can be written as 15/100. This directly reflects the definition of percentage – 15 parts out of 100.
-
Simplify the fraction: To simplify a fraction, you need to find the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. In this case, the GCD of 15 and 100 is 5.
-
Divide both the numerator and the denominator by the GCD: Dividing both 15 and 100 by 5, we get:
15 ÷ 5 = 3 100 ÷ 5 = 20
Therefore, the simplified fraction is 3/20. This means 15% is equivalent to 3 parts out of 20 equal parts.
Alternative Methods and Further Exploration
While the above method is the most straightforward, let's explore a few alternative approaches to reinforce understanding:
-
Using Decimal Conversion: You can first convert the percentage to a decimal by dividing it by 100. 15% divided by 100 is 0.15. Then, convert the decimal to a fraction. 0.15 can be written as 15/100, which simplifies to 3/20, as shown above.
-
Understanding Proportions: The relationship between 15% and its fractional equivalent can be understood through proportions. We know that 15% is 15 out of 100. We can set up a proportion:
15/100 = x/y
If we let y = 20 (a convenient denominator for simplification), we can solve for x:
15/100 = x/20
Cross-multiplying gives us:
100x = 300
Solving for x:
x = 3
Thus, the equivalent fraction is 3/20. This method highlights the proportional relationship between percentages and fractions.
-
Visual Representation: Imagine a circle divided into 100 equal parts. Shading 15 of those parts visually represents 15%. If you then group those shaded parts into sets of 5, you'll have 3 sets out of 20 sets, again illustrating the 3/20 fraction.
Practical Applications and Real-World Examples
The conversion of percentages to fractions is crucial in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, and tax amounts often involves converting percentages to fractions for accurate calculations. For example, a 15% discount on a $100 item means a reduction of (3/20) * $100 = $15.
-
Cooking and Baking: Recipes frequently use percentages to indicate the proportion of ingredients. Converting these percentages to fractions can simplify the measuring process, especially when dealing with smaller quantities.
-
Science: Data analysis in scientific experiments often involves working with percentages and fractions to represent proportions and probabilities.
-
Construction and Engineering: Calculations related to material quantities, area measurements, and structural design may involve percentage-to-fraction conversions for precise calculations.
Frequently Asked Questions (FAQ)
Q: Can all percentages be easily converted to simple fractions?
A: No. While many percentages can be simplified to relatively simple fractions, some may result in more complex fractions that cannot be easily simplified further. For instance, 17% converts to 17/100, which is already in its simplest form.
Q: What if I have a percentage with a decimal, like 15.5%?
A: You can follow the same steps, but you'll end up with a more complex fraction. 15.5% becomes 15.5/100. To simplify, multiply both numerator and denominator by 10 to remove the decimal: 155/1000. This simplifies to 31/200.
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to understand and work with. A simplified fraction provides the most concise representation of the proportion.
Q: Are there any online tools or calculators that can help with this conversion?
A: While this article provides a thorough explanation allowing for manual calculation, many online calculators are available that can perform percentage-to-fraction conversions quickly. However, understanding the underlying process is far more valuable than relying solely on calculators.
Conclusion
Converting 15% to a fraction, resulting in 3/20, is a fundamental skill in mathematics with broad applications. This article has gone beyond simply providing the answer, aiming to enhance your understanding of percentages, fractions, and the conversion process. By exploring different methods, practical examples, and addressing frequently asked questions, we've built a solid foundation for you to confidently tackle similar problems and apply these skills in diverse contexts. Remember, mastering these concepts is crucial for success in various fields, fostering numerical literacy and problem-solving abilities. Practice these conversions regularly, and you'll quickly develop proficiency and a deeper understanding of the underlying mathematical principles.
Latest Posts
Latest Posts
-
Find An Equation For The Plane Through The Points
Aug 28, 2025
-
Sketch The Region Corresponding To The Statement
Aug 28, 2025
-
How Much Is A Half Inch
Aug 28, 2025
-
The Product Of 7 And The Square Of A Number
Aug 28, 2025
-
Is The Nclex The Same In Every State
Aug 28, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Percent As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.