What Is 1/3 Cup Times 2
faraar
Sep 19, 2025 · 6 min read
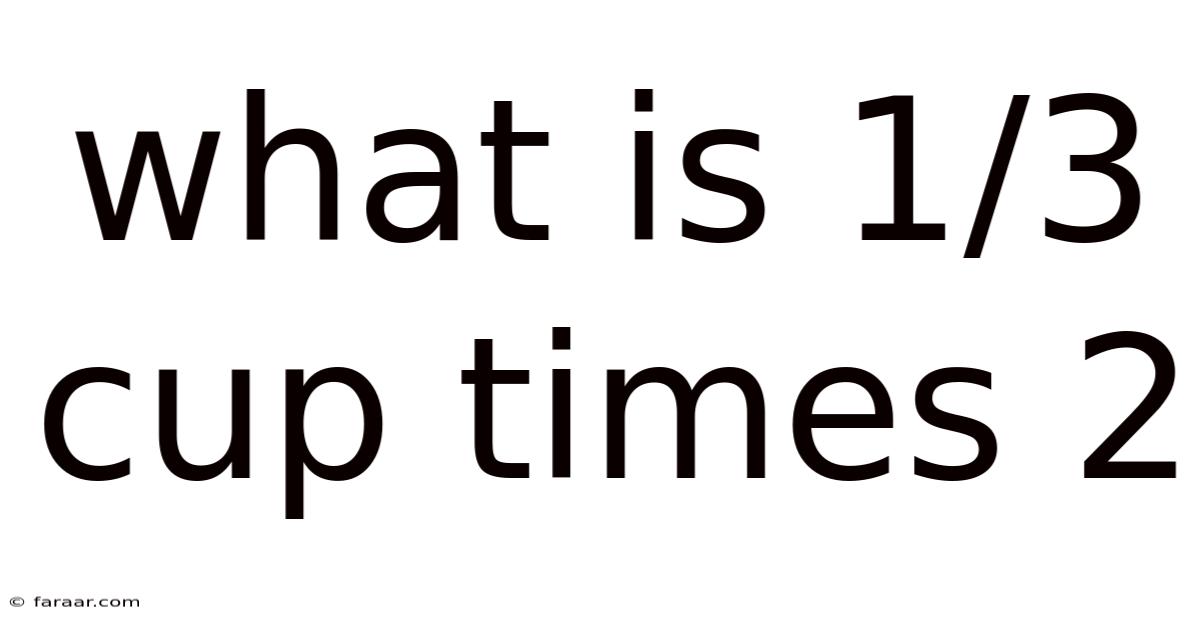
Table of Contents
What is 1/3 Cup Times 2? A Deep Dive into Fractions and Measurement
This article will explore the seemingly simple question: "What is 1/3 cup times 2?" While the answer might seem immediately obvious to some, we'll delve deeper into the underlying mathematical principles, practical applications in cooking and baking, and common misconceptions surrounding fraction multiplication. Understanding this seemingly basic calculation is crucial for anyone working with recipes, conducting scientific experiments involving measurements, or simply improving their grasp of fundamental mathematics. We'll cover various methods to solve this problem and extend the knowledge to more complex fraction calculations.
Understanding Fractions: A Refresher
Before we tackle the problem of 1/3 cup times 2, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. In our case, 1/3 represents one part out of three equal parts.
Visualizing fractions can be incredibly helpful. Imagine a pie cut into three equal slices. 1/3 of the pie represents one of those slices. 2/3 would represent two slices, and 3/3 would represent the entire pie. This visual representation helps to solidify the concept of fractions and makes understanding operations on them easier.
Multiplying Fractions: The Simple Approach
Multiplying fractions is a straightforward process. To multiply two fractions, we simply multiply the numerators together and then multiply the denominators together. Let's apply this to our problem: 1/3 cup times 2.
We can rewrite 2 as a fraction: 2/1. Now our problem becomes: (1/3) * (2/1).
Following the rule for multiplying fractions:
- Numerator: 1 * 2 = 2
- Denominator: 3 * 1 = 3
Therefore, 1/3 cup times 2 is equal to 2/3 cup.
Visualizing 1/3 Cup Times 2
Let's reinforce this concept visually. Imagine you have a measuring cup divided into thirds. 1/3 cup represents one of those thirds. If you double that amount, you have two of those thirds, which is precisely 2/3 of a cup. This simple visualization helps connect the abstract mathematical operation to a concrete, real-world scenario.
Applying this to Cooking and Baking
Understanding fraction multiplication is essential in cooking and baking. Recipes often require precise measurements, and being able to quickly and accurately calculate fractional amounts is crucial for achieving desired results. Imagine a recipe calling for 1/3 cup of sugar. If you need to double the recipe, knowing that 1/3 cup times 2 equals 2/3 cup allows you to accurately measure the correct amount of sugar. This precision prevents mistakes and ensures the final product tastes as intended.
Dealing with Mixed Numbers
Sometimes, recipes or other measurements might involve mixed numbers – a combination of a whole number and a fraction (e.g., 1 1/2 cups). Let's explore how to handle such scenarios when multiplying by a fraction.
Suppose we need to calculate 1 1/2 cups times 1/3. First, we need to convert the mixed number into an improper fraction. To do this, we multiply the whole number by the denominator and add the numerator, then place the result over the original denominator.
1 1/2 becomes (1 * 2 + 1) / 2 = 3/2
Now we multiply the improper fraction by 1/3:
(3/2) * (1/3) = 3/6
This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 3:
3/6 = 1/2
Therefore, 1 1/2 cups times 1/3 is equal to 1/2 cup.
More Complex Fraction Multiplication
The principles discussed above extend to more complex fraction multiplication problems. For instance, consider multiplying 2/5 cup by 3/4.
(2/5) * (3/4) = (2 * 3) / (5 * 4) = 6/20
This fraction can be simplified to 3/10.
This demonstrates that the basic principle of multiplying numerators and denominators remains consistent, even with more complex fractions. Remember to always simplify your final answer to its lowest terms.
Common Misconceptions about Fraction Multiplication
A frequent mistake when working with fractions is confusing multiplication with addition or subtraction. Remember that multiplying fractions involves multiplying the numerators and the denominators separately. Adding or subtracting fractions requires finding a common denominator first.
Another common error is forgetting to simplify the final answer. Always check if the resulting fraction can be simplified by finding the greatest common divisor of the numerator and denominator. This ensures your answer is presented in its simplest and most understandable form.
Practical Applications Beyond Cooking
The ability to multiply fractions isn't limited to culinary arts. This skill is vital in various fields:
- Construction and Engineering: Precise measurements are essential for accurate construction. Fractions are frequently used in blueprints and calculations.
- Science and Medicine: Scientific experiments often involve precise measurements and dilutions, requiring a strong understanding of fraction manipulation.
- Finance: Calculating percentages, interest rates, and proportions frequently involves working with fractions.
- Sewing and Tailoring: Accurate measurements are essential for pattern making and garment construction.
Mastering fraction multiplication equips you with a valuable skill applicable across numerous disciplines.
Frequently Asked Questions (FAQ)
Q: What if I need to multiply 1/3 cup by a number that isn't a whole number, like 2.5?
A: Convert the decimal number (2.5) into a fraction (5/2). Then, multiply the fractions as usual: (1/3) * (5/2) = 5/6.
Q: How do I convert an improper fraction back to a mixed number?
A: Divide the numerator by the denominator. The quotient becomes the whole number, the remainder becomes the numerator, and the denominator stays the same. For example, 5/6 remains as 5/6 (it's already a proper fraction), but 7/3 would be 2 1/3 (7 divided by 3 is 2 with a remainder of 1).
Q: Are there online tools or calculators that can help with fraction multiplication?
A: Yes, many online calculators and tools are readily available to assist with fraction calculations. These can be particularly useful for more complex problems or for double-checking your work.
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes them easier to understand and compare. It's also essential for consistency in calculations and presentations.
Conclusion: Mastering Fractions for a Brighter Future
This in-depth exploration of the seemingly simple question "What is 1/3 cup times 2?" has revealed the underlying mathematical principles and their significant practical applications. Understanding fraction multiplication is not just about solving mathematical problems; it's a fundamental skill with far-reaching implications in various aspects of life, from cooking and baking to construction and science. By mastering these concepts, you equip yourself with a valuable tool for accurate measurements, problem-solving, and a more profound understanding of the world around you. The ability to confidently work with fractions opens doors to more complex mathematical concepts and enhances your overall problem-solving skills, laying a strong foundation for future learning and success. Remember the simple steps, practice regularly, and embrace the power of fractions!
Latest Posts
Latest Posts
-
Electric Guitar Lessons Near Me For Beginners
Sep 19, 2025
-
Distributive Property And Order Of Operations
Sep 19, 2025
-
Which Statement Describes A Chemical Reaction
Sep 19, 2025
-
How Many Cups Is 1 Pound Of Pecans
Sep 19, 2025
-
Give The Products Of The Reaction
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/3 Cup Times 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.