What Is 1 2 Of 1 2 3
faraar
Aug 27, 2025 · 5 min read
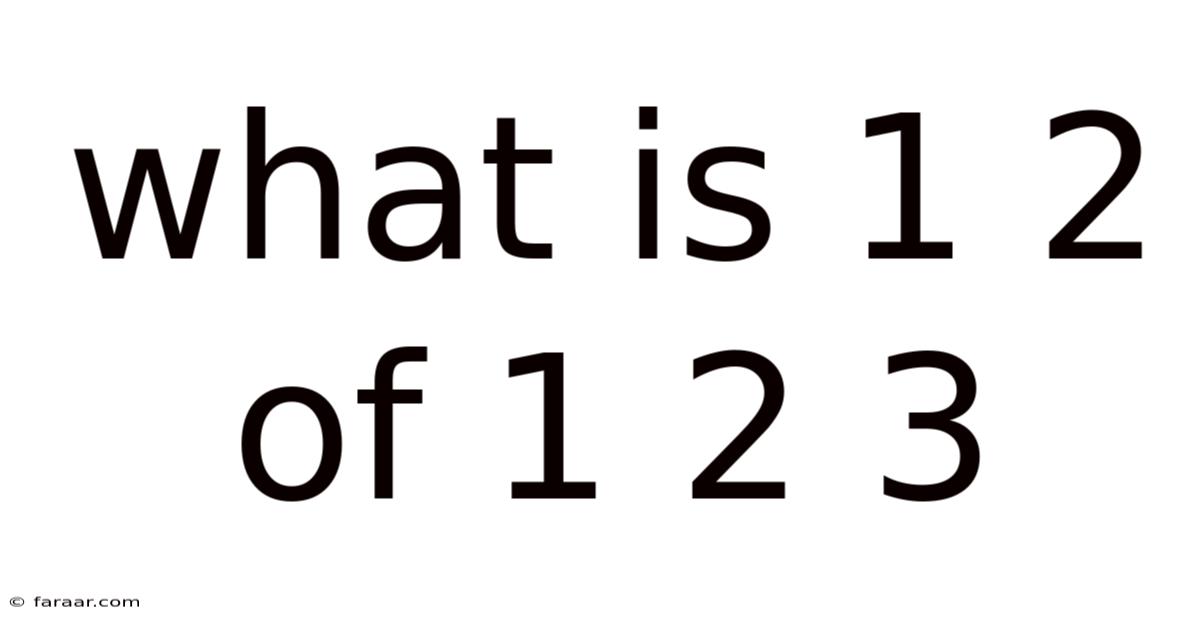
Table of Contents
Decoding the Enigma: What is 1/2 of 1/2 + 3? A Comprehensive Guide to Fraction Arithmetic
This article will delve into the seemingly simple yet often confusing problem of calculating "1/2 of 1/2 + 3". We'll break down the process step-by-step, exploring the underlying principles of fraction arithmetic and order of operations, ensuring a complete understanding for readers of all mathematical backgrounds. This comprehensive guide will not only provide the solution but also equip you with the skills to tackle similar problems confidently.
Understanding the Problem: Order of Operations (PEMDAS/BODMAS)
Before diving into the calculations, let's address the fundamental principle governing the order in which we perform mathematical operations. This principle is often remembered using the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Both acronyms represent the same hierarchy of operations.
In our problem, "1/2 of 1/2 + 3," the word "of" signifies multiplication. Therefore, the problem can be rewritten as:
(1/2) * (1/2) + 3
Following PEMDAS/BODMAS, we must first perform the multiplication before the addition.
Step-by-Step Calculation: Mastering Fraction Multiplication and Addition
1. Multiplying Fractions:
The multiplication of two fractions is straightforward: we multiply the numerators (top numbers) together and the denominators (bottom numbers) together.
(1/2) * (1/2) = (1 * 1) / (2 * 2) = 1/4
2. Adding Fractions and Whole Numbers:
Now, we need to add 1/4 to 3. To do this efficiently, we need to express both numbers with a common denominator. Since 3 can be expressed as 3/1, we convert it to a fraction with a denominator of 4:
3/1 = (3 * 4) / (1 * 4) = 12/4
Now we can add the fractions:
1/4 + 12/4 = (1 + 12) / 4 = 13/4
3. Simplifying the Result (if necessary):
In this case, the fraction 13/4 is already in its simplest form. However, if the resulting fraction could be simplified (e.g., 6/8 could be simplified to 3/4), it's crucial to do so for accuracy and clarity.
Therefore, the answer to "1/2 of 1/2 + 3" is 13/4 or 3 1/4.
Alternative Approaches: Visualizing Fractions
While the numerical approach is efficient, understanding the concept visually can enhance comprehension, especially for beginners. Let's visualize the problem using area models.
Imagine a square representing 1 whole unit. 1/2 of this square would be half the area. Now, taking 1/2 of that 1/2 (1/2 * 1/2) means finding one-half of the half-square, resulting in a smaller area representing 1/4 of the whole square. Adding 3 to this 1/4 represents adding three whole squares to the 1/4 section, resulting in a total area equivalent to 3 and 1/4 squares.
This visual representation reinforces the numerical answer obtained previously.
The Importance of Parentheses (Brackets): A Deeper Dive
The correct use of parentheses is crucial in mathematics. They dictate the order of operations and prevent ambiguity. Consider this slightly modified problem:
1/2 of (1/2 + 3)
Here, the parentheses indicate that we must first add 1/2 and 3 before multiplying by 1/2. This changes the calculation significantly:
1/2 + 3 = 3 1/2 = 7/2
Now, we multiply 7/2 by 1/2:
(1/2) * (7/2) = 7/4 = 1 3/4
This example highlights the importance of carefully observing the placement of parentheses (or brackets) in mathematical expressions. A slight change in the arrangement completely alters the outcome.
Expanding the Knowledge: Working with Different Fractions
Let's extend our understanding by tackling a similar problem with different fractions:
2/3 of 3/4 + 5
1. Multiplication:
(2/3) * (3/4) = (2 * 3) / (3 * 4) = 6/12
2. Simplification:
6/12 can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 6:
6/12 = 1/2
3. Addition:
1/2 + 5 = 5 1/2 = 11/2
Therefore, 2/3 of 3/4 + 5 = 11/2 or 5 1/2.
Tackling More Complex Scenarios: Mixed Numbers and Decimals
The principles we've explored also extend to problems involving mixed numbers (a whole number and a fraction) and decimals. Let's consider:
1.5 of 2.25 + 4
First, convert decimals to fractions:
1.5 = 3/2 2.25 = 9/4
Now the calculation becomes:
(3/2) * (9/4) + 4 = 27/8 + 4
Convert 4 to a fraction with a denominator of 8:
4 = 32/8
Now add the fractions:
27/8 + 32/8 = 59/8
This can be expressed as a mixed number:
59/8 = 7 3/8
Or as a decimal:
59/8 = 7.375
This demonstrates the adaptability of the core principles to various numerical representations.
Frequently Asked Questions (FAQ)
-
Q: What if the "of" is replaced by a division symbol?
- A: This would drastically change the problem. If the problem was 1/2 ÷ 1/2 +3, the division would be performed first according to PEMDAS/BODMAS, resulting in a different answer. 1/2 ÷ 1/2 = 1, then 1 + 3 = 4.
-
Q: Are there any other methods to solve fraction problems?
- A: Yes, you can use decimal equivalents. Converting fractions to decimals can sometimes simplify the calculation, particularly for those more comfortable with decimal arithmetic. However, it's essential to maintain precision during conversion.
-
Q: How can I improve my skills in fraction arithmetic?
- A: Consistent practice is key. Work through various problems, starting with simpler ones and gradually increasing the complexity. Use online resources, textbooks, or work with a tutor for personalized guidance.
Conclusion: Mastering Fractions for a Stronger Mathematical Foundation
Understanding fraction arithmetic is crucial for a solid foundation in mathematics. The problem "1/2 of 1/2 + 3" might seem simple at first glance, but it provides a valuable opportunity to reinforce the principles of order of operations, fraction multiplication, and addition. By breaking down the problem step-by-step and visualizing the process, we not only arrive at the correct solution (13/4 or 3 1/4) but also gain a deeper understanding of the fundamental concepts involved. Mastering these skills will empower you to confidently tackle more complex mathematical challenges in the future. Remember to practice regularly and seek clarification whenever needed to build a strong and lasting understanding of this essential mathematical area.
Latest Posts
Latest Posts
-
What Is The Perimeter Of Abcd
Aug 27, 2025
-
Write A Polynomial In Standard Form
Aug 27, 2025
-
How To Find The Variable In An Equation
Aug 27, 2025
-
What Is 2 Divided By 1 4
Aug 27, 2025
-
Consider The Mechanism Step 1 2a
Aug 27, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 2 Of 1 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.