What Divided By 6 Equals 9
faraar
Sep 21, 2025 · 5 min read
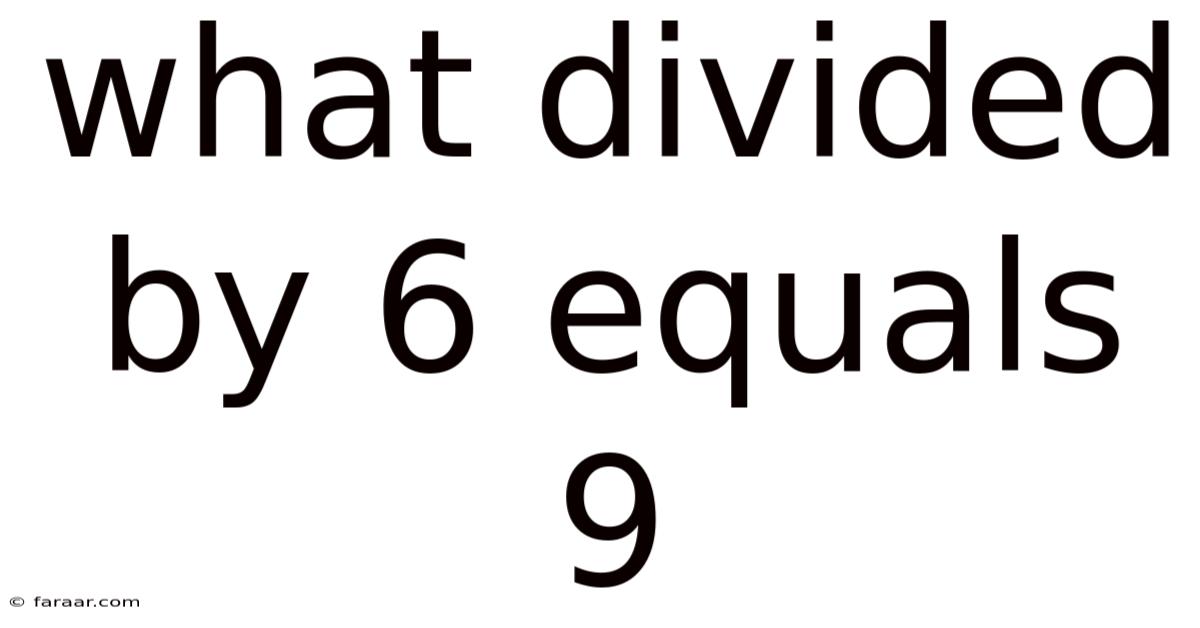
Table of Contents
What Divided by 6 Equals 9? Unlocking the Mystery of Division
This article explores the seemingly simple yet conceptually rich question: "What divided by 6 equals 9?" We'll delve into the mathematical solution, explore the underlying principles of division, and examine how this seemingly basic problem can help us understand more complex mathematical concepts. We'll also address common misconceptions and frequently asked questions to ensure a comprehensive understanding.
Understanding the Problem: A Foundation in Division
Before jumping into the solution, let's refresh our understanding of division. Division is essentially the inverse operation of multiplication. When we say "What divided by 6 equals 9?", we're essentially asking: "What number, when divided into six equal parts, results in 9 for each part?" This can be represented algebraically as:
x / 6 = 9
Where 'x' is the unknown number we're trying to find.
Solving the Equation: Finding the Missing Number
To solve for 'x', we need to isolate it on one side of the equation. The inverse operation of division is multiplication. Therefore, we multiply both sides of the equation by 6:
(x / 6) * 6 = 9 * 6
This simplifies to:
x = 54
Therefore, 54 divided by 6 equals 9.
Beyond the Answer: Exploring the Concepts
While finding the answer (54) is straightforward, let's delve deeper into the concepts illustrated by this problem:
-
Inverse Operations: This problem highlights the crucial relationship between division and multiplication. They are inverse operations, meaning one undoes the other. This principle is fundamental to solving many algebraic equations.
-
Understanding Quotients and Divisors: In the equation x / 6 = 9, 'x' represents the dividend, 6 is the divisor, and 9 is the quotient. Understanding these terms is crucial for comprehending division problems and interpreting results in various contexts.
-
Real-World Applications: Division is used extensively in everyday life. Consider sharing 54 cookies equally among 6 friends. Each friend would receive 9 cookies. This simple example demonstrates the practical application of division in real-world scenarios.
-
Fractions and Division: Division is intrinsically linked to fractions. The problem x / 6 = 9 can also be represented as the fraction x/6 = 9/1. This highlights the equivalence between division and expressing a quantity as a fraction.
Expanding the Understanding: Variations and Extensions
Let's explore some variations and extensions of the problem to solidify our understanding:
-
Changing the Divisor: What if the problem was "What divided by 3 equals 9?" Following the same method, we would multiply both sides by 3, resulting in x = 27. This demonstrates how changing the divisor alters the solution.
-
Changing the Quotient: What if the problem was "What divided by 6 equals 12?" Again, applying the same principle, we multiply both sides by 6, giving x = 72. This shows how a change in the quotient impacts the solution.
-
Word Problems: Let's consider a word problem: "A baker made a certain number of loaves of bread. After dividing them equally among 6 shelves, there were 9 loaves on each shelf. How many loaves did the baker make?" This is essentially the same problem, but presented in a real-world context, reinforcing the practical application of division.
The Importance of Practice and Application
Mastering division, and indeed any mathematical concept, requires consistent practice and application. Working through various problems, both simple and complex, is crucial for developing a strong understanding. Start with simple problems like "What divided by 6 equals 9?" and gradually progress to more challenging problems that involve multiple steps and different mathematical operations.
Addressing Common Misconceptions
Several common misconceptions surround division. Let's address a few:
-
Order of Operations: Division doesn't always come before multiplication. The order of operations (PEMDAS/BODMAS) dictates the sequence of calculations. Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
-
Dividing by Zero: It's crucial to remember that division by zero is undefined. There is no number that can be multiplied by zero to produce a non-zero result. This concept is fundamental to understanding the limitations of division.
-
Negative Numbers: Division involving negative numbers follows the same rules as positive numbers, but with careful consideration of signs. Remember that a negative number divided by a positive number results in a negative number, and vice versa. A negative number divided by a negative number results in a positive number.
Frequently Asked Questions (FAQ)
Q: What if the equation was 6 divided by x equals 9?
A: This is a slightly different problem. Here, we have 6/x = 9. To solve, we multiply both sides by 'x' and then divide both sides by 9, resulting in x = 2/3 or 0.666...
Q: Can this problem be solved using other methods besides the direct algebraic approach?
A: Yes, you could use iterative methods or even trial and error. However, the algebraic approach provides a more efficient and systematic solution.
Q: How can I improve my understanding of division?
A: Consistent practice is key. Work through various problems, starting with simple examples and gradually increasing the complexity. Use real-world examples to connect the concept to practical applications. Explore different representations of division, such as fractions and long division.
Q: Are there any online resources that can help me practice division?
A: Numerous websites and educational apps offer interactive exercises and tutorials on division. These resources can provide valuable practice and feedback.
Conclusion: The Power of Understanding Division
The seemingly simple question, "What divided by 6 equals 9?", offers a gateway to a deeper understanding of division, its relationship with multiplication, and its numerous applications in various fields. By exploring the solution, understanding the underlying principles, and addressing common misconceptions, we can appreciate the power and versatility of this fundamental mathematical operation. Remember, consistent practice and application are key to mastering division and unlocking its potential in solving more complex mathematical problems. The journey from a simple equation to a comprehensive understanding highlights the beauty and elegance of mathematics.
Latest Posts
Latest Posts
-
Heat Denatures A Protein By Disrupting
Sep 21, 2025
-
Is Kcn An Acid Or Base
Sep 21, 2025
-
How To Convert Parametric To Rectangular
Sep 21, 2025
-
60 Of What Number Is 27
Sep 21, 2025
-
Does A Rectangle Have Congruent Sides
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about What Divided By 6 Equals 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.