What Are The Measures Of Angles B And C
faraar
Sep 07, 2025 · 6 min read
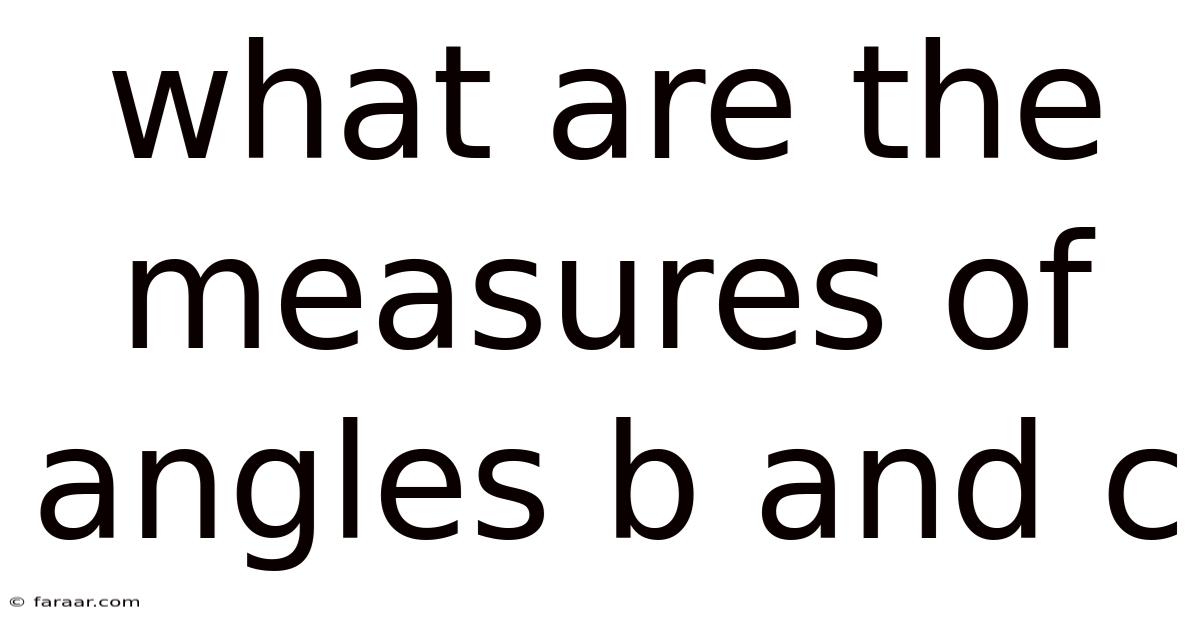
Table of Contents
Unlocking the Secrets of Angles B and C: A Comprehensive Guide to Angle Measurement
Determining the measures of angles B and C in a geometric context requires understanding the relationships between angles within a given shape or configuration. This article will explore various scenarios, from simple triangles to more complex polygons and their associated theorems, providing a thorough understanding of how to calculate angles B and C. We will delve into the fundamental principles, offering practical examples and explanations suitable for learners of all levels. Whether you're tackling a geometry problem, designing a structure, or simply curious about the mathematics of angles, this guide will equip you with the knowledge to confidently solve for angles B and C in a variety of situations.
Understanding Basic Angle Relationships
Before we delve into specific examples, it's crucial to review some fundamental concepts. Angles are measured in degrees (°), with a full circle encompassing 360°. Several key angle relationships are essential for solving for unknown angles:
- Complementary Angles: Two angles are complementary if their sum is 90°.
- Supplementary Angles: Two angles are supplementary if their sum is 180°.
- Vertical Angles: Vertical angles are the angles opposite each other when two lines intersect. They are always equal.
- Adjacent Angles: Adjacent angles share a common vertex and side.
Calculating Angles B and C in Triangles
Triangles, with their three sides and three angles, are a fundamental building block in geometry. The sum of angles in any triangle always equals 180°. This crucial property allows us to determine the measure of an unknown angle if we know the measures of the other two.
Example 1: An Isosceles Triangle
Let's consider an isosceles triangle where angle A is 40°, and angles B and C are equal. We can solve for B and C using the following steps:
- Apply the Triangle Angle Sum Theorem: A + B + C = 180°
- Substitute the known angle: 40° + B + C = 180°
- Use the Isosceles Triangle Property: Since B = C, we can rewrite the equation as: 40° + 2B = 180°
- Solve for B: 2B = 180° - 40° = 140° => B = 70°
- Determine C: Since B = C, C = 70°
Therefore, in this isosceles triangle, angles B and C both measure 70°.
Example 2: A Right-Angled Triangle
In a right-angled triangle, one angle is always 90°. If angle A is 90° and angle B is 35°, we can find angle C:
- Apply the Triangle Angle Sum Theorem: A + B + C = 180°
- Substitute the known angles: 90° + 35° + C = 180°
- Solve for C: C = 180° - 90° - 35° = 55°
Thus, angle C measures 55°.
Calculating Angles B and C in Other Polygons
The principles of angle calculation extend beyond triangles. For polygons with more than three sides, the sum of interior angles is given by the formula (n-2) * 180°, where 'n' is the number of sides.
Example 3: A Quadrilateral
Consider a quadrilateral with angles A, B, C, and D. If A = 70°, B = 110°, and C = 90°, we can find angle D:
- Calculate the sum of interior angles: (4-2) * 180° = 360°
- Apply the sum of interior angles: A + B + C + D = 360°
- Substitute known angles: 70° + 110° + 90° + D = 360°
- Solve for D: D = 360° - 70° - 110° - 90° = 90°
Therefore, angle D measures 90°. This approach can be applied to any polygon, irrespective of its shape or the equality of its angles.
Advanced Techniques: Trigonometry and Similar Triangles
For more complex scenarios, trigonometry plays a crucial role. Trigonometric functions like sine, cosine, and tangent relate the angles of a right-angled triangle to the lengths of its sides. If you know the lengths of certain sides and an angle, you can utilize these functions to solve for unknown angles.
- Sine (sin): Opposite side / Hypotenuse
- Cosine (cos): Adjacent side / Hypotenuse
- Tangent (tan): Opposite side / Adjacent side
Example 4: Using Trigonometry
In a right-angled triangle, if the length of the side opposite angle B is 5 units and the hypotenuse is 10 units, we can find angle B:
- Apply the sine function: sin(B) = Opposite / Hypotenuse = 5/10 = 0.5
- Use the inverse sine function: B = sin⁻¹(0.5) = 30°
Therefore, angle B measures 30°. Similar techniques can be applied using cosine and tangent functions depending on the available information.
Similar triangles also provide a powerful tool for angle calculation. If two triangles are similar, their corresponding angles are equal. This property can be used to solve for unknown angles in one triangle if the angles of a similar triangle are known.
Practical Applications and Real-World Examples
The ability to measure and calculate angles is crucial across numerous disciplines:
- Architecture and Engineering: Calculating angles is essential in structural design, ensuring stability and functionality.
- Surveying: Accurate angle measurement is critical for land surveying and mapping.
- Navigation: Angles are used extensively in navigation, both on land and sea, to determine directions and positions.
- Computer Graphics: In computer graphics and animation, understanding angles is fundamental for creating realistic images and movements.
- Astronomy: Angles are used extensively to measure the positions and movements of celestial objects.
Frequently Asked Questions (FAQs)
- Q: What happens if I have more than one unknown angle?
A: If you have multiple unknown angles, you’ll need multiple equations to solve the problem. These equations might come from the properties of specific shapes (like triangles adding up to 180 degrees), or from the relationships between angles (like supplementary or complementary angles). Often, a combination of geometric theorems and algebraic manipulation will be required.
- Q: Can I use a protractor to find the measure of angles?
A: Yes, a protractor is a useful tool for measuring angles directly. However, it is important to note that a protractor offers an approximate measurement, whereas mathematical calculations will provide a precise value. Protractors are best suited for practical applications where perfect accuracy is not always required.
- Q: Are there any online tools or calculators that can help me calculate angles?
A: Many online calculators and geometry software packages can assist in angle calculations. These tools can significantly aid in solving complex problems and checking your work. However, understanding the underlying principles is crucial to effectively use these tools and to gain a deeper understanding of geometry.
Conclusion
Calculating the measures of angles B and C, whether in simple triangles or more complex polygons, relies on a thorough understanding of fundamental geometric principles and their applications. By mastering the concepts of complementary, supplementary, and vertical angles, the triangle angle sum theorem, and utilizing trigonometry when appropriate, you can confidently solve for unknown angles in a variety of situations. Remember that practice is key – the more you work with these concepts, the more intuitive they become. As you progress, you will develop a strong foundation in geometry and an appreciation for the elegance and power of mathematical problem-solving. This ability extends far beyond the classroom, proving valuable in various real-world applications and disciplines. Remember to always double-check your work and consider using multiple methods to verify your results. Geometry, while sometimes challenging, is a rewarding field to explore.
Latest Posts
Latest Posts
-
Greatest Common Factor Of 54 And 27
Sep 08, 2025
-
How To Find R In A Scatter Plot
Sep 08, 2025
-
Finding Amplitude Period And Phase Shift
Sep 08, 2025
-
A Playground Ride Consists Of A Disk Of Mass
Sep 08, 2025
-
Which Is A Set Of Valid Quantum Numbers
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about What Are The Measures Of Angles B And C . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.