V Pie R 2h Solve For R
faraar
Sep 15, 2025 · 6 min read
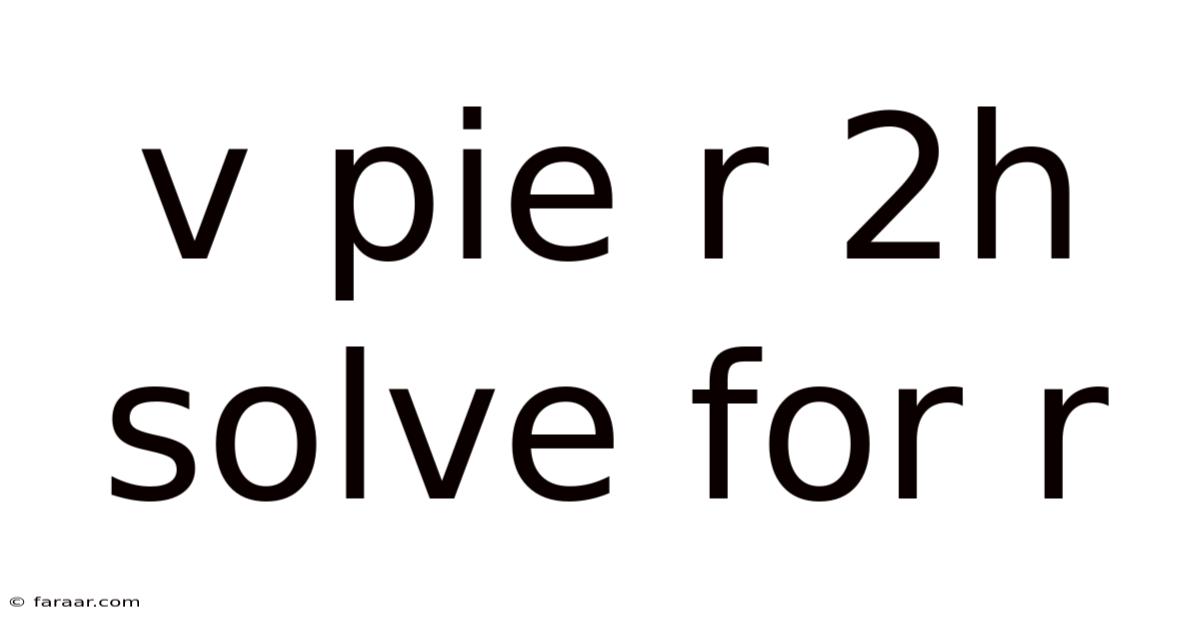
Table of Contents
Solving for r: Unveiling the Radius in the Volume of a Cylinder
Understanding the formula for the volume of a cylinder, V = πr²h, is fundamental in various fields, from engineering and architecture to mathematics and physics. This equation relates the volume (V) of a cylinder to its radius (r) and height (h). Often, you'll need to rearrange this formula to solve for a specific variable, particularly the radius (r). This article provides a comprehensive guide on how to solve for r in V = πr²h, explaining the steps, the underlying mathematical principles, and offering practical examples to solidify your understanding. We'll also explore common mistakes and address frequently asked questions.
Understanding the Volume of a Cylinder Formula
Before diving into the solution, let's clarify the components of the formula: V = πr²h
-
V: Represents the volume of the cylinder, typically measured in cubic units (e.g., cubic centimeters, cubic meters). Volume indicates the amount of three-dimensional space occupied by the cylinder.
-
π (Pi): A mathematical constant, approximately equal to 3.14159. Pi represents the ratio of a circle's circumference to its diameter and is crucial in calculating the area of a circle, which forms the base of the cylinder.
-
r: Represents the radius of the cylinder's circular base. The radius is the distance from the center of the circle to any point on the circle's edge.
-
h: Represents the height of the cylinder. The height is the perpendicular distance between the two circular bases.
The formula itself indicates that the volume of a cylinder is the product of the area of its circular base (πr²) and its height (h).
Solving for r: A Step-by-Step Guide
To solve for 'r' in the equation V = πr²h, we need to isolate 'r' on one side of the equation. This involves a series of algebraic manipulations. Here's the step-by-step process:
Step 1: Divide both sides by πh
Our goal is to isolate r². To do this, we begin by dividing both sides of the equation by πh. This maintains the equality of the equation.
V / (πh) = (πr²h) / (πh)
This simplifies to:
V / (πh) = r²
Step 2: Take the square root of both sides
Now that we have r², we need to find 'r'. To do this, we take the square root of both sides of the equation. Remember that when taking the square root, we consider both the positive and negative roots. However, since 'r' represents a radius (a physical distance), we only consider the positive square root.
√(V / (πh)) = √(r²)
This simplifies to:
r = √(V / (πh))
Therefore, the solution for 'r' is: r = √(V / (πh))
This formula allows us to calculate the radius of a cylinder if we know its volume and height.
Practical Examples: Applying the Formula
Let's illustrate the process with a few examples:
Example 1:
A cylinder has a volume of 150 cubic centimeters and a height of 10 centimeters. Find its radius.
-
Substitute the known values: V = 150 cm³, h = 10 cm. π ≈ 3.14159
-
Apply the formula: r = √(V / (πh)) = √(150 cm³ / (3.14159 * 10 cm))
-
Calculate: r ≈ √(4.7746) cm ≈ 2.18 cm
Therefore, the radius of the cylinder is approximately 2.18 centimeters.
Example 2:
A cylindrical water tank has a volume of 5000 liters and a height of 2 meters. Find its radius. (Note: 1 cubic meter = 1000 liters)
-
Convert units: First, convert the volume to cubic meters: 5000 liters / 1000 liters/m³ = 5 m³
-
Substitute the known values: V = 5 m³, h = 2 m. π ≈ 3.14159
-
Apply the formula: r = √(V / (πh)) = √(5 m³ / (3.14159 * 2 m))
-
Calculate: r ≈ √(0.79577) m ≈ 0.89 m
Therefore, the radius of the water tank is approximately 0.89 meters.
Mathematical Explanation: Understanding the Steps
The solution process relies on fundamental algebraic principles:
-
Equality: Any operation performed on one side of an equation must be performed on the other side to maintain the equality. This is crucial in steps 1 and 2 where we divide and take the square root of both sides.
-
Inverse Operations: We use inverse operations to isolate the variable 'r'. Division is the inverse of multiplication (to get rid of 'h'), and the square root is the inverse of squaring (to get rid of the exponent 2).
-
Order of Operations (PEMDAS/BODMAS): Remember the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) when performing calculations. This ensures accurate results.
Common Mistakes and How to Avoid Them
Several common mistakes can occur when solving for 'r':
-
Incorrect Order of Operations: Forgetting the order of operations, especially when dealing with multiple operations in the formula, can lead to incorrect results. Always follow PEMDAS/BODMAS.
-
Errors in Calculation: Careless mistakes in arithmetic calculations (division, square root) are frequent. Use a calculator and double-check your work.
-
Forgetting the Square Root: Failing to take the square root in step 2 leads to finding r² instead of r.
-
Unit Conversion Errors: Inconsistent or incorrect unit conversions (e.g., mixing centimeters and meters) can significantly affect the accuracy of your answer. Always ensure consistent units throughout the calculation.
Frequently Asked Questions (FAQs)
Q1: What if the volume or height is zero?
If either the volume (V) or height (h) is zero, the formula becomes undefined. A cylinder cannot exist with zero volume or zero height.
Q2: Can the radius be negative?
No. The radius represents a physical distance, and distance cannot be negative. We only consider the positive square root.
Q3: What if I have a cylinder with an oblique height (not perpendicular to the base)?
The formula V = πr²h only applies to right circular cylinders where the height is perpendicular to the base. For oblique cylinders, a more complex calculation is needed involving trigonometry.
Q4: How accurate are the results?
The accuracy of the results depends on the accuracy of the input values (V and h) and the precision used for π. Using more decimal places for π will increase accuracy.
Q5: Are there any other ways to find the radius of a cylinder?
Yes, if you know the circumference (C) of the base, you can use the formula C = 2πr to find the radius. Other methods might involve measuring the diameter (d) and using the relationship r = d/2.
Conclusion
Solving for the radius (r) in the volume of a cylinder formula, V = πr²h, is a straightforward process once you understand the underlying algebraic principles and follow the steps carefully. This formula has wide-ranging applications in various fields. By mastering this calculation, you'll enhance your problem-solving skills in mathematics and improve your understanding of geometrical concepts. Remember to double-check your calculations, pay attention to units, and always consider the physical meaning of the results. Consistent practice with different examples will solidify your understanding and improve your proficiency in solving for the radius of cylinders.
Latest Posts
Latest Posts
-
Half Of 5 1 2 Inches
Sep 15, 2025
-
How To Shut Up In Spanish
Sep 15, 2025
-
How Do You Calculate The Mass Of Water
Sep 15, 2025
-
A 9y 3yx Solve For Y
Sep 15, 2025
-
Use Synthetic Division To Find The Quotient And The Remainder
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about V Pie R 2h Solve For R . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.