V 1 3 Πr2h Solve For H
faraar
Sep 09, 2025 · 5 min read
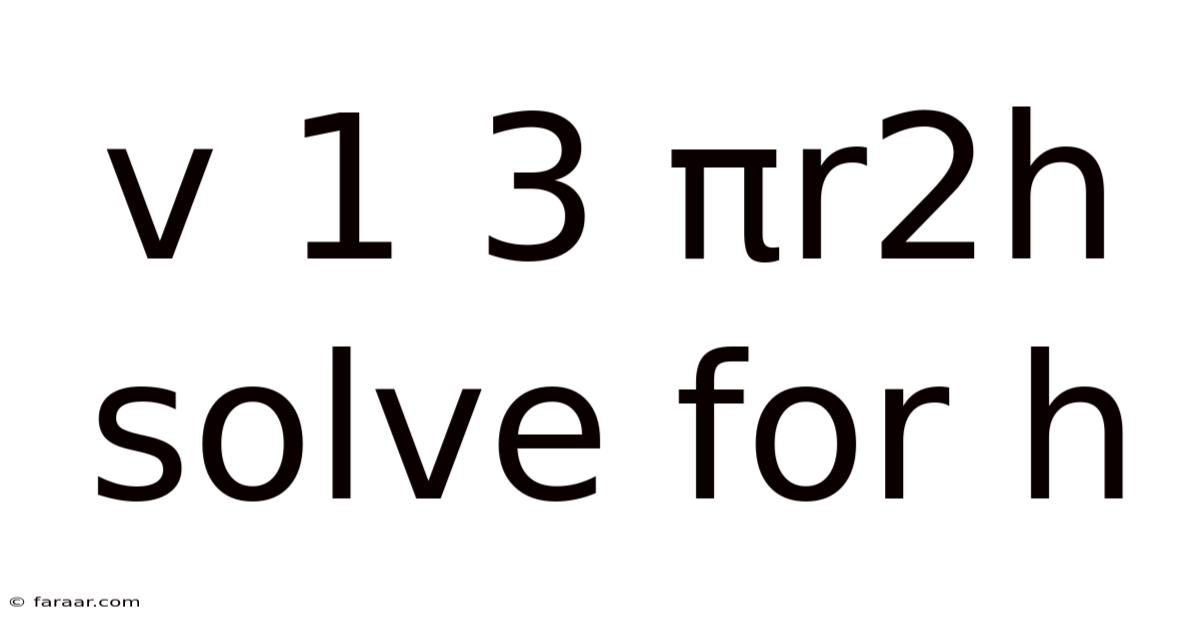
Table of Contents
Solving for h: Unraveling the Volume of a Cylinder
Understanding the formula for the volume of a cylinder, V = πr²h, is a fundamental concept in geometry. This formula allows us to calculate the volume of cylindrical objects—from soda cans to grain silos—given their radius (r) and height (h). But what if we know the volume and radius, and we need to find the height? This article will guide you through the process of solving for 'h' in the equation V = πr²h, providing a step-by-step explanation, scientific underpinnings, and addressing frequently asked questions.
Understanding the Variables
Before diving into the solution, let's clarify the variables in the formula:
-
V: Represents the volume of the cylinder. Volume is the amount of three-dimensional space occupied by an object. It's typically measured in cubic units (e.g., cubic centimeters, cubic meters, cubic inches).
-
π (Pi): A mathematical constant, approximately equal to 3.14159. Pi represents the ratio of a circle's circumference to its diameter and is crucial in many geometrical calculations involving circles and cylinders.
-
r: Represents the radius of the cylinder's circular base. The radius is the distance from the center of the circle to any point on the circumference.
-
h: Represents the height of the cylinder. This is the perpendicular distance between the two circular bases.
The formula V = πr²h essentially states that the volume of a cylinder is found by multiplying the area of its circular base (πr²) by its height (h).
Solving for h: A Step-by-Step Guide
Our goal is to isolate 'h' on one side of the equation. Here's how we do it:
-
Start with the original formula: V = πr²h
-
Divide both sides by πr²: To isolate 'h', we need to get rid of π and r². Since πr² is multiplying 'h', we perform the inverse operation – division. This gives us:
V / (πr²) = h
-
Rearrange the equation: Conventionally, we write the variable we're solving for on the left-hand side. Therefore, the final solution is:
h = V / (πr²)
This formula now allows us to calculate the height (h) of a cylinder if we know its volume (V) and radius (r).
Illustrative Example
Let's solidify our understanding with an example. Imagine a cylindrical water tank with a known volume of 100 cubic meters and a radius of 2 meters. To find the height of the tank, we'll substitute the values into our derived formula:
h = V / (πr²)
h = 100 m³ / (π * (2 m)²)
h ≈ 100 m³ / (3.14159 * 4 m²)
h ≈ 100 m³ / 12.566 m²
h ≈ 7.96 meters
Therefore, the height of the water tank is approximately 7.96 meters.
The Scientific Underpinnings: Derivation from Calculus
The formula V = πr²h isn't just a random equation; it's derived from fundamental principles of calculus. The volume of a cylinder can be visualized as an infinite stack of infinitesimally thin circular disks. The volume of each disk is given by the area of the circle (πr²) multiplied by its infinitesimal thickness (dh). To find the total volume, we integrate this expression over the height of the cylinder:
∫₀ʰ πr² dh
Since πr² is a constant with respect to h, the integral simplifies to:
πr² ∫₀ʰ dh = πr² [h]₀ʰ = πr²h
This integral confirms the validity of the formula V = πr²h, highlighting the connection between geometry and calculus.
Practical Applications
The ability to solve for 'h' in the equation V = πr²h has wide-ranging applications across various fields:
-
Engineering: Calculating the height of cylindrical structures like tanks, silos, pipes, or columns, given their volume and radius.
-
Manufacturing: Determining the height required for cylindrical containers or components based on their volume and radius specifications.
-
Architecture: Designing cylindrical structures with specific volume requirements, such as water towers or cylindrical rooms.
-
Physics: Solving problems related to fluid mechanics involving cylindrical vessels.
-
Everyday Life: Estimating the height of cylindrical objects like cans, bottles, or even trees (approximating them as cylinders).
Frequently Asked Questions (FAQ)
Q1: What if I only know the volume and height, and I need to find the radius?
A1: To solve for the radius (r), you would rearrange the formula as follows:
r = √(V / (πh))
You need to take the square root because the radius is squared in the original equation.
Q2: How do I handle units when using this formula?
A2: Ensure that all your units are consistent. If the volume is in cubic meters, the radius should be in meters, and the resulting height will also be in meters. Using inconsistent units will lead to incorrect results.
Q3: What if the cylinder is not perfectly cylindrical?
A3: The formula V = πr²h only applies to perfect cylinders with uniform radius and height. For irregularly shaped objects, more complex methods, such as integration techniques from calculus, might be necessary.
Q4: Can I use this formula for other shapes?
A4: No, this formula is specifically derived for cylinders. Other shapes, like cones or spheres, have different volume formulas.
Q5: Are there online calculators to help with this?
A5: Yes, many online calculators are available that can quickly calculate the height of a cylinder given its volume and radius. However, understanding the underlying formula is crucial for problem-solving and application beyond simple calculations.
Conclusion
Solving for 'h' in the equation V = πr²h is a straightforward yet essential skill in various scientific and engineering disciplines. This article has provided a comprehensive guide, including a step-by-step solution, illustrative examples, and a glimpse into the underlying scientific principles. By mastering this concept, you will be better equipped to tackle various real-world problems involving cylindrical volumes and geometries. Remember to always maintain consistent units and consider the limitations of the formula when applied to non-ideal cylindrical shapes. The ability to manipulate and understand this fundamental geometrical formula will undoubtedly enhance your problem-solving skills and broaden your understanding of the world around you.
Latest Posts
Latest Posts
-
Is Blood A Compound Or Mixture
Sep 10, 2025
-
One On One Tutors Near Me
Sep 10, 2025
-
What Is The Value Of Y When X 2
Sep 10, 2025
-
Find The Perimeter Of Quadrilateral Abcd
Sep 10, 2025
-
Hazel Eyes And Brown Eyes Parents
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about V 1 3 Πr2h Solve For H . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.