Two More Than 4 Times A Number Is
faraar
Aug 26, 2025 · 5 min read
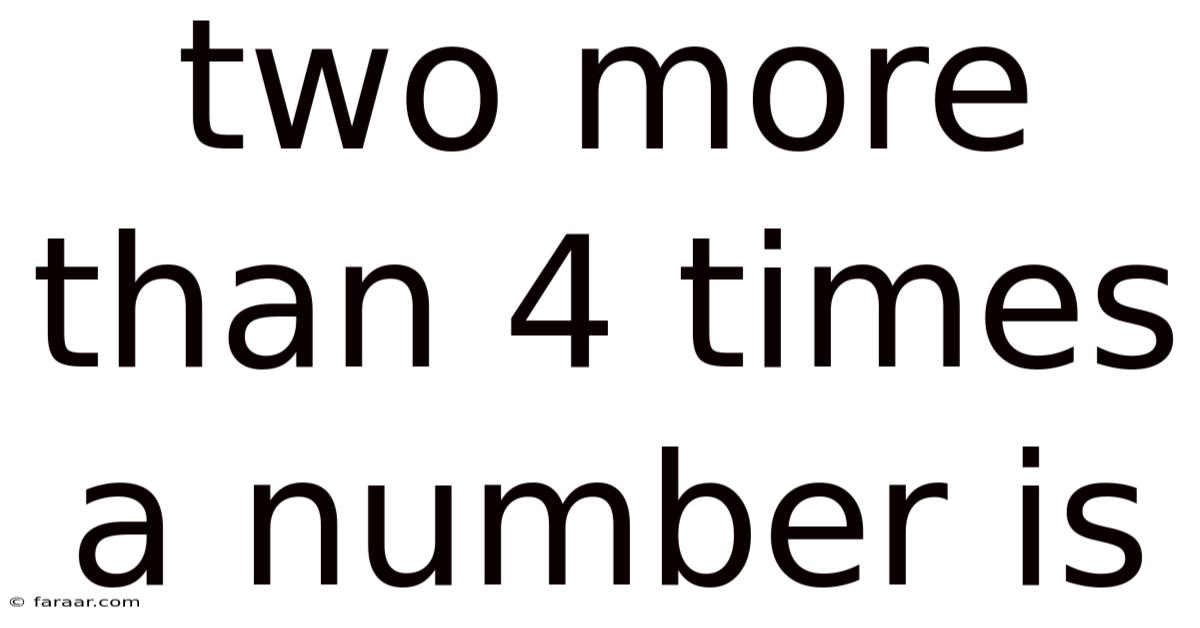
Table of Contents
Two More Than 4 Times a Number: Unraveling the Mystery of Algebraic Expressions
Understanding algebraic expressions is fundamental to success in mathematics. This article delves into the seemingly simple phrase, "two more than 4 times a number," transforming it from a verbal statement into a powerful algebraic equation and exploring its applications. We'll cover how to translate words into mathematical symbols, solve equations related to this expression, and finally, apply this knowledge to real-world problems. By the end, you'll not only comprehend this specific expression but also gain a broader understanding of algebraic manipulation and problem-solving strategies.
Introduction: From Words to Symbols
The phrase "two more than 4 times a number" might seem intimidating at first glance, but it's actually quite straightforward once you break it down. The key is to translate each part of the phrase into mathematical symbols. Let's dissect it step-by-step:
-
"a number": This represents an unknown value, which we typically denote with a variable, such as x, y, or n. For simplicity, let's use x.
-
"4 times a number": This translates directly to 4 * x, or more concisely, 4x. This means we're multiplying the unknown number (x) by 4.
-
"two more than": This indicates addition. We're adding 2 to the result of "4 times a number."
Therefore, the complete algebraic expression for "two more than 4 times a number" is 4x + 2. This simple expression forms the foundation for many mathematical problems.
Building and Solving Equations
Now that we've translated the phrase into an algebraic expression, we can use it to create and solve equations. An equation is a statement that shows two expressions are equal. Let's consider a few examples:
Example 1: Finding the Number
Suppose "two more than 4 times a number is 14." This translates into the equation:
4x + 2 = 14
To solve for x, we follow these steps:
-
Subtract 2 from both sides: This isolates the term with x. 4x + 2 - 2 = 14 - 2 4x = 12
-
Divide both sides by 4: This solves for x. 4x / 4 = 12 / 4 x = 3
Therefore, the number is 3. We can check our answer by substituting x = 3 back into the original equation: 4(3) + 2 = 14, which is true.
Example 2: A More Complex Scenario
Let's consider a slightly more complex problem: "Two more than 4 times a number is equal to 3 less than 7 times the same number." This translates to:
4x + 2 = 7x - 3
Solving this equation involves several steps:
-
Subtract 4x from both sides: This moves all terms with x to one side. 4x + 2 - 4x = 7x - 3 - 4x 2 = 3x - 3
-
Add 3 to both sides: This isolates the term with x. 2 + 3 = 3x - 3 + 3 5 = 3x
-
Divide both sides by 3: This solves for x. 5 / 3 = 3x / 3 x = 5/3 or 1.666...
In this case, the number is 5/3 (or approximately 1.67).
Real-World Applications: Putting it into Practice
The expression "two more than 4 times a number" isn't just an abstract mathematical concept; it has numerous real-world applications. Consider these examples:
-
Pricing and Discounts: A store might offer a discount where the final price is "two dollars more than four times the discounted price." If the final price is $22, you could set up an equation to find the discounted price.
-
Geometry: The perimeter of a rectangle might be expressed as "two more than four times its width," allowing you to solve for the width given the perimeter.
-
Physics: Certain physics problems, particularly those involving motion or forces, might involve expressions similar to "two more than four times a certain velocity."
-
Finance: Simple interest calculations sometimes involve expressions of this form, relating principal, interest rate, and time.
Expanding the Concept: Variations and Extensions
The core concept of "two more than 4 times a number" can be expanded to include more complex scenarios. We can alter the numbers, introduce additional operations, or incorporate multiple variables. For example:
-
"Five more than three times a number": This would be represented by the expression 3x + 5.
-
"Two less than twice a number": This would be represented by the expression 2x - 2.
-
"The sum of two numbers, where one is two more than four times the other": This would involve two variables, say x and y, with y = 4x + 2.
Understanding the Order of Operations (PEMDAS/BODMAS)
It's crucial to remember the order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). In our expression 4x + 2, multiplication (4x) is performed before addition (+2). Ignoring the order of operations would lead to incorrect results.
Frequently Asked Questions (FAQs)
Q1: What if the phrase was "four times a number more than two"?
A1: This is a subtly different phrasing. It would be represented as 2 + 4x, which is equivalent to 4x + 2 because addition is commutative (the order doesn't matter).
Q2: Can this expression be used with negative numbers?
A2: Absolutely! The variable x can represent any real number, including negative values.
Q3: How can I improve my skills in solving algebraic equations?
A3: Practice is key! Work through various problems of increasing difficulty, focusing on understanding each step and checking your answers. Use online resources, textbooks, or seek help from a tutor if needed.
Q4: Are there any other ways to represent "two more than 4 times a number"?
A4: While 4x + 2 is the most straightforward representation, you could also write it as 2 + 4x, or even as 4(x + 1/2) – although this latter form isn't as intuitive.
Conclusion: Mastering Algebraic Expressions
Understanding how to translate verbal phrases into algebraic expressions is a vital skill in mathematics and beyond. The seemingly simple phrase "two more than 4 times a number" provides a perfect starting point for developing this crucial skill. By breaking down the phrase, building equations, solving for unknowns, and applying this knowledge to real-world examples, we’ve demonstrated the power and practicality of algebraic manipulation. Remember to practice consistently, and you'll soon master the art of translating words into mathematical symbols and solving the resulting equations with confidence. This foundational understanding will pave the way for tackling more complex mathematical problems and unlocking a deeper appreciation for the elegance and power of algebra.
Latest Posts
Latest Posts
-
How Do You Solve X 2
Aug 26, 2025
-
Is 2 3 Cups More Than 1 2
Aug 26, 2025
-
Pressure Of Water At 20 C
Aug 26, 2025
-
Can You Use A Calculator On The Teas Test
Aug 26, 2025
-
How Many Gram Sugar In A Teaspoon
Aug 26, 2025
Related Post
Thank you for visiting our website which covers about Two More Than 4 Times A Number Is . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.