The Volume Of The Box Is 18 Cubic Centimeters
faraar
Sep 07, 2025 · 6 min read
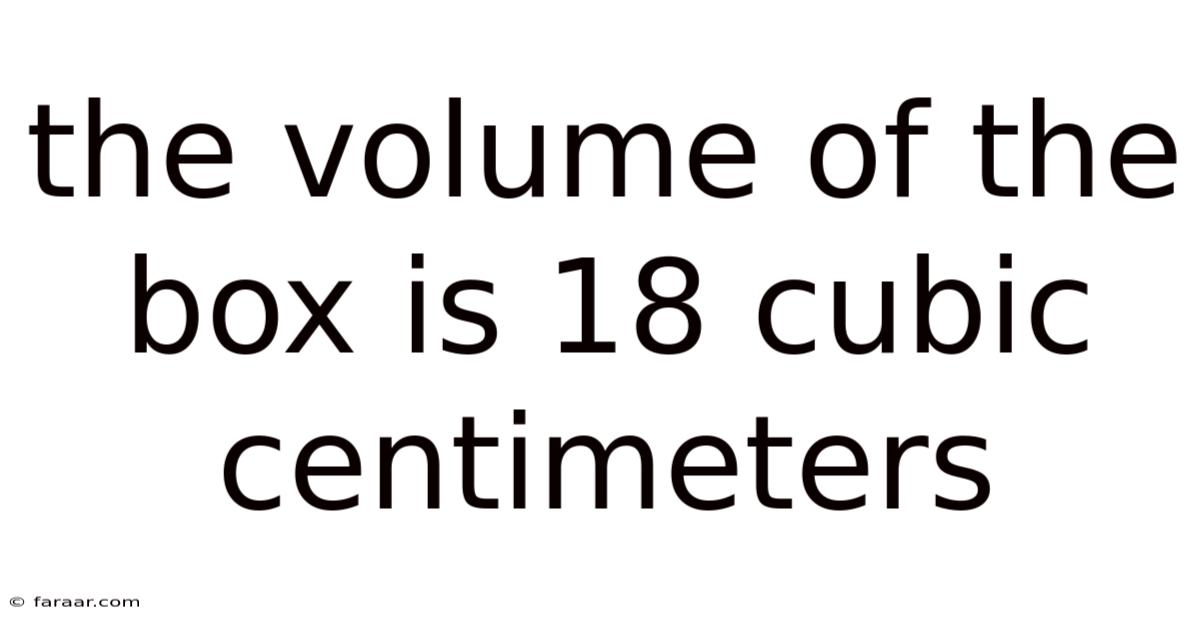
Table of Contents
Unpacking the Mystery: Exploring the Dimensions of a 18 Cubic Centimeter Box
The seemingly simple statement, "the volume of the box is 18 cubic centimeters," opens up a world of mathematical exploration and practical considerations. This seemingly small volume holds within it a surprising range of possibilities and invites us to delve into the fascinating relationship between volume, surface area, and the three dimensions of length, width, and height. This article will explore different approaches to determining the possible dimensions of such a box, discuss the implications of varying dimensions on surface area and material cost, and even touch on the practical applications of such calculations.
Understanding Volume and Cubic Centimeters
Before we embark on our exploration, let's clarify the fundamental concept of volume. Volume is the amount of three-dimensional space occupied by an object or substance. In our case, we're dealing with a box, which is a rectangular prism. The volume of a rectangular prism is calculated by multiplying its length (l), width (w), and height (h): Volume = l × w × h. The unit "cubic centimeters" (cm³) indicates that the volume is measured in cubes with sides of 1 centimeter each. Therefore, a box with a volume of 18 cm³ means it can hold 18 of these 1 cm³ cubes.
Finding the Dimensions: A Mathematical Journey
The challenge lies in the fact that there isn't one unique solution to the equation l × w × h = 18. This simple equation has numerous integer solutions, and even more solutions if we consider decimal values. Let's explore some of these possibilities:
-
Integer Solutions: We can start by looking for whole number solutions. A systematic approach involves listing factors of 18. The factors of 18 are 1, 2, 3, 6, 9, and 18. By systematically combining these factors, we can find several integer solutions:
- 1 cm × 1 cm × 18 cm
- 1 cm × 2 cm × 9 cm
- 1 cm × 3 cm × 6 cm
- 2 cm × 3 cm × 3 cm
-
Decimal Solutions: The possibilities expand dramatically when we consider decimal values for length, width, and height. For instance, we could have dimensions like 1.5 cm × 2 cm × 6 cm, or 2.5 cm × 1.5 cm × 4.8 cm, and countless others. The number of potential decimal solutions is infinite.
-
Visualizing the Possibilities: It's helpful to visualize these different box shapes. Imagine a long, thin box (1 cm × 1 cm × 18 cm) versus a more cube-like box (2 cm × 3 cm × 3 cm). These variations have significant implications for other properties of the box.
Beyond Volume: Exploring Surface Area
While volume tells us the space inside the box, the surface area tells us the total area of its exterior faces. This is crucial when considering the amount of material needed to construct the box or the cost associated with it. The surface area of a rectangular prism is calculated using the formula: Surface Area = 2(lw + lh + wh).
Let's calculate the surface area for a few of our integer solutions:
- 1 cm × 1 cm × 18 cm: Surface Area = 2(1 + 18 + 18) = 74 cm²
- 1 cm × 2 cm × 9 cm: Surface Area = 2(2 + 9 + 18) = 58 cm²
- 1 cm × 3 cm × 6 cm: Surface Area = 2(3 + 6 + 18) = 54 cm²
- 2 cm × 3 cm × 3 cm: Surface Area = 2(6 + 6 + 9) = 42 cm²
Notice that the surface area varies significantly depending on the dimensions, even though the volume remains constant. This illustrates the important trade-off between volume and surface area. A box with a smaller surface area (like the 2 cm × 3 cm × 3 cm box) will generally require less material to construct, leading to lower costs.
Practical Applications and Real-World Considerations
Understanding the relationship between volume and dimensions has numerous practical applications:
-
Packaging and Shipping: Companies must carefully design packaging to minimize material usage while ensuring product protection. Optimizing the dimensions of a box for a given volume can significantly reduce costs and environmental impact.
-
Construction and Engineering: Calculations involving volume are fundamental in construction projects, from estimating the amount of concrete needed for a foundation to determining the capacity of storage tanks.
-
Manufacturing: Manufacturers need to consider volume and dimensions when designing products and molds. Optimizing dimensions can lead to efficiency gains in production and material usage.
-
Chemistry and Physics: Volume is a critical parameter in many scientific experiments and calculations. Understanding volume and its relationship to dimensions is essential in fields such as chemistry, where precise measurements are crucial.
The Importance of Optimization
Given the many possible dimensions for a box with a volume of 18 cm³, the question arises: which dimensions are optimal? The answer depends on the specific application and the criteria for optimization. Some possible criteria include:
-
Minimizing surface area: This is crucial for minimizing material costs and waste. The 2 cm × 3 cm × 3 cm box, with its surface area of 42 cm², is the most efficient in this regard among the integer solutions we've explored.
-
Maximizing length or width: In some applications, one dimension might be more important than others. For example, if the box needs to fit into a specific space, the length or width might need to be maximized.
-
Practical considerations: The dimensions also need to be practically feasible. Very thin or long boxes might be difficult to handle or stack.
Frequently Asked Questions (FAQ)
Q: Are there any limits to the number of possible dimensions for a box with a volume of 18 cm³?
A: No, there are infinitely many possible dimensions if we consider decimal values for length, width, and height.
Q: How does the shape of the box affect its strength?
A: The shape significantly impacts the box's structural strength. A more cube-like shape generally provides greater stability and strength than a long, thin box.
Q: What if the box isn't a perfect rectangular prism?
A: If the box has a different shape (e.g., a triangular prism, cylinder), the volume calculation will be different, and the relationship between volume and dimensions will change accordingly.
Q: Can I use this information to design my own packaging?
A: Yes, this knowledge is a crucial starting point for packaging design. You'll need to consider factors such as product dimensions, shipping requirements, and material costs to optimize the box's dimensions for your specific needs.
Conclusion: Beyond the Numbers
The seemingly simple problem of a box with a volume of 18 cubic centimeters leads us down a path of mathematical exploration, practical considerations, and an appreciation for the interplay between geometry and real-world applications. While there are infinitely many possible solutions, understanding the principles of volume, surface area, and optimization allows us to choose the dimensions that best suit our specific needs. This seemingly small volume, therefore, holds within it a wealth of information and potential applications, reminding us that even simple mathematical problems can have far-reaching implications. The key is to approach the problem systematically, understanding the underlying principles, and adapting the solution to the specific context. By considering these factors, we can move beyond simply finding solutions to truly understanding and optimizing the design of our 18 cubic centimeter box.
Latest Posts
Latest Posts
-
Length Of Diagonal Of A Box
Sep 07, 2025
-
Difference Between Persuasive Essay And Argumentative Essay
Sep 07, 2025
-
What Molecule Absorbs Sunlight For Photosynthesis
Sep 07, 2025
-
What Is The Measure Of Angle Abd
Sep 07, 2025
-
How To Find Secant Line Slope
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about The Volume Of The Box Is 18 Cubic Centimeters . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.