The Sum Of A Number And 12
faraar
Sep 21, 2025 · 5 min read
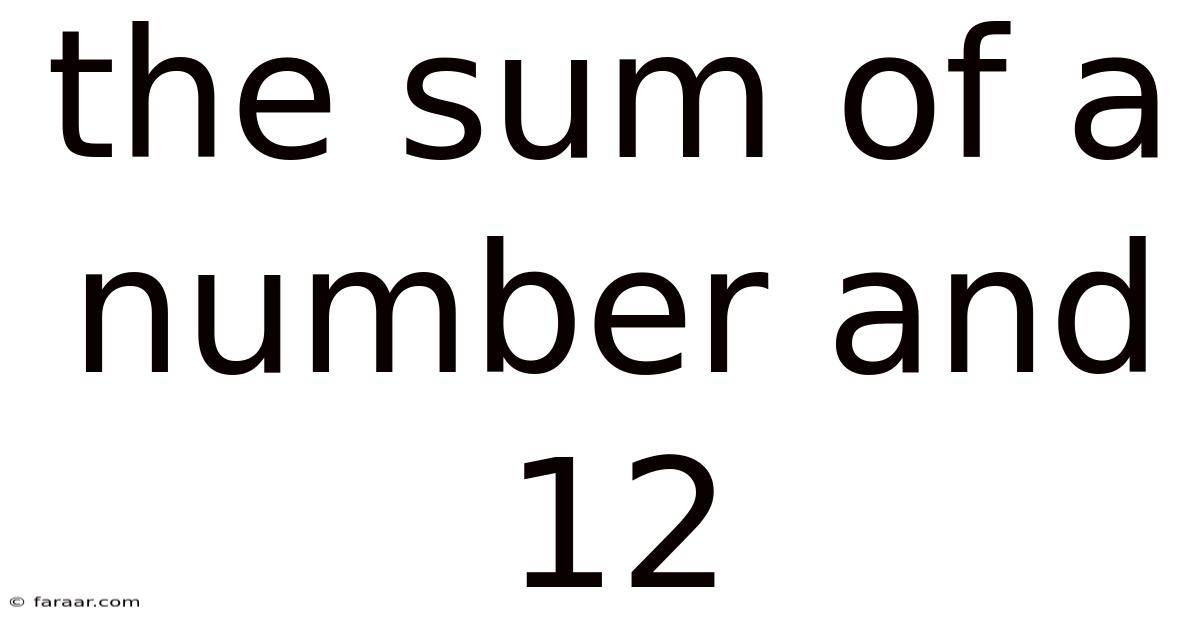
Table of Contents
Exploring the Sum of a Number and 12: A Deep Dive into Addition and its Applications
The seemingly simple concept of "the sum of a number and 12" opens a door to a vast world of mathematical exploration. This seemingly basic arithmetic operation forms the foundation for countless more complex calculations and concepts, spanning from elementary school arithmetic to advanced calculus. This article will delve into this fundamental concept, exploring its practical applications, theoretical underpinnings, and extensions into more advanced mathematical realms. We'll cover various approaches to understanding and solving problems involving this sum, catering to a wide range of mathematical backgrounds.
Introduction: Understanding the Basics
At its core, "the sum of a number and 12" simply means adding 12 to an unknown number. This unknown number is often represented by a variable, typically x. Therefore, the expression can be written algebraically as x + 12. This seemingly straightforward expression provides a springboard for understanding more complex mathematical operations and problem-solving techniques. The beauty of this simple expression lies in its versatility; it can be used to represent a wide array of real-world scenarios.
Representing Real-World Scenarios with x + 12
The power of algebraic representation lies in its ability to model real-world problems. Let's consider a few examples:
-
Scenario 1: Profit Calculation: Imagine a small business owner who earns $12 profit for every item they sell. If they sell x items, their total profit can be represented as x + 12. This assumes a fixed additional profit of $12 regardless of the number of items sold. This scenario can be adapted to include variable costs or other income streams to create more complex profit models.
-
Scenario 2: Temperature Increase: If the current temperature is x degrees Celsius, and it increases by 12 degrees, the new temperature is x + 12 degrees Celsius. This applies to any scenario involving an incremental increase in a measurable quantity.
-
Scenario 3: Collecting Items: Suppose you already have 12 stamps in your collection, and you acquire x more. The total number of stamps you possess is represented by x + 12. This can be extended to any type of collectible or inventory management system.
-
Scenario 4: Age Calculation: If someone is x years old now, their age in 12 years will be x + 12 years. This straightforward expression has implications in various fields like actuarial science and demographics.
These examples highlight the versatility of the expression x + 12 in representing various real-world problems involving addition. The ability to translate these real-world scenarios into mathematical expressions is a crucial skill in applied mathematics.
Solving Equations Involving x + 12
Often, we're not just presented with the expression x + 12, but with an equation involving this expression. This means we need to find the value of x that satisfies the equation. Let’s explore a few examples:
- Example 1: x + 12 = 20
To solve this, we subtract 12 from both sides of the equation to isolate x:
x + 12 - 12 = 20 - 12
x = 8
Therefore, the value of x that satisfies the equation is 8.
- Example 2: x + 12 = -5
Following the same procedure:
x + 12 - 12 = -5 - 12
x = -17
This demonstrates that x can be a negative number.
- Example 3: 2x + 12 = 30
This equation involves a coefficient of 2 before x. We first subtract 12 from both sides:
2x + 12 - 12 = 30 - 12
2x = 18
Then, we divide both sides by 2:
2x / 2 = 18 / 2
x = 9
These examples showcase the fundamental principles of solving linear equations, where the goal is always to isolate the variable x.
Advanced Applications and Extensions
The simple expression x + 12 serves as a building block for more complex mathematical concepts:
-
Functions: We can represent this sum as a function: f(x) = x + 12. This function maps any input value x to its sum with 12. This forms the basis for understanding linear functions and their properties.
-
Sequences and Series: The expression can be used to define arithmetic sequences. For example, the sequence 12, 24, 36, 48... can be represented by the formula a_n = 12n, where a_n is the nth term in the sequence. This connects our simple expression to concepts within number theory.
-
Calculus: The derivative of the function f(x) = x + 12 is simply 1, indicating a constant rate of change. This highlights the connection between elementary algebra and the concepts of differential calculus.
-
Linear Algebra: The expression can be viewed as a simple linear transformation, where a vector is added to a constant vector [12]. This establishes a link between basic arithmetic and the more abstract concepts of linear algebra.
Frequently Asked Questions (FAQs)
-
Q: What if the number added to 12 is a decimal or fraction?
A: The process remains the same. You simply perform the addition according to the rules of decimal or fractional arithmetic. For example, 3.5 + 12 = 15.5 and (1/2) + 12 = 12.5.
-
Q: Can the sum of a number and 12 ever be negative?
A: Yes, if the number is less than -12. For instance, if x = -15, then x + 12 = -3.
-
Q: How can I check if my answer is correct when solving an equation involving x + 12?
A: Substitute the value you found for x back into the original equation. If the equation holds true, your answer is correct.
-
Q: Are there any real-world applications beyond those already mentioned?
A: Many! Think about situations involving budgeting, calculating distances, combining quantities, or any scenario that requires adding a fixed value to a variable quantity.
Conclusion: The Enduring Significance of a Simple Sum
The seemingly simple concept of "the sum of a number and 12" is far more profound than it first appears. It serves as a foundational building block in mathematics, underpinning numerous complex concepts and providing a framework for modeling a wide array of real-world situations. From elementary arithmetic to advanced calculus, this simple addition operation reveals its importance in diverse fields, demonstrating the power and elegance inherent in even the most basic mathematical principles. By understanding this fundamental concept thoroughly, we pave the way for mastering more complex mathematical challenges and enhancing our ability to solve problems in diverse areas of life. The journey from understanding a simple addition to comprehending its advanced applications showcases the fascinating interconnectedness of mathematical concepts and their vast applicability in the real world.
Latest Posts
Latest Posts
-
Does A Rhombus Have Four Congruent Sides
Sep 21, 2025
-
Are The Two Lines Parallel Perpendicular Or Neither
Sep 21, 2025
-
How Many Calories Are In A 16 Inch Pizza
Sep 21, 2025
-
Musical Theater Voice Lessons Near Me
Sep 21, 2025
-
A Conflict Is A Struggle Between
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about The Sum Of A Number And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.