The Sum Of 7 And X
faraar
Sep 14, 2025 · 6 min read
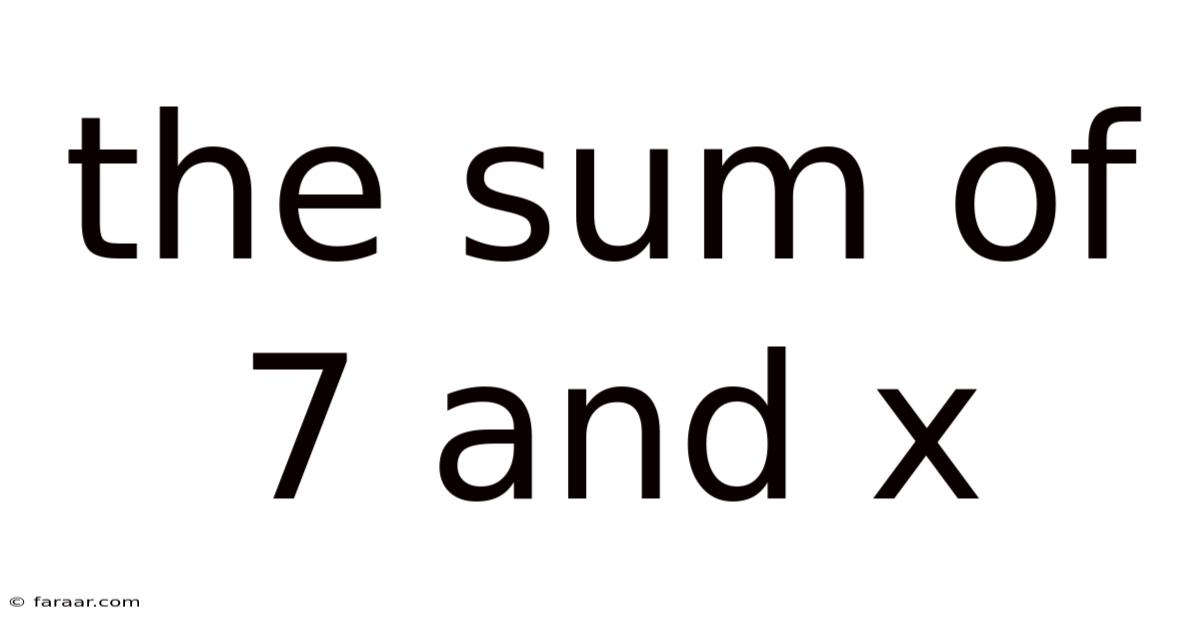
Table of Contents
Exploring the Sum of 7 and x: A Deep Dive into Algebraic Expressions
The seemingly simple expression "the sum of 7 and x" opens a door to a vast world of mathematical concepts. While it might appear rudimentary at first glance, understanding this expression provides a foundational stepping stone to grasping more complex algebraic manipulations, equations, and problem-solving techniques. This article will explore this expression in depth, moving from its basic interpretation to advanced applications, ensuring a comprehensive understanding suitable for learners of all levels.
Introduction: What is the Sum of 7 and x?
At its core, "the sum of 7 and x" represents an algebraic expression. It signifies the result of adding the number 7 to an unknown variable, represented by the letter 'x'. The 'x' can represent any real number – positive, negative, fractional, or even zero. The expression itself, 7 + x, doesn't provide a numerical answer; instead, it offers a formula or a generalized representation of the sum. To obtain a numerical answer, we would need to assign a specific value to 'x'. This simple expression is fundamental to algebra and forms the basis for countless mathematical operations and problem-solving scenarios.
Understanding Variables and Constants
Before delving deeper, let's clarify the difference between a variable and a constant. In our expression, 7 is a constant – its value remains fixed and unchanging. 'x', on the other hand, is a variable – its value can vary or change depending on the context of the problem. Understanding this distinction is crucial for interpreting and manipulating algebraic expressions correctly.
Representing the Sum of 7 and x in Different Forms
The sum of 7 and x can be represented in several ways, all mathematically equivalent:
- 7 + x: This is the most straightforward and commonly used representation.
- x + 7: The commutative property of addition states that the order of the terms doesn't affect the sum. Therefore, x + 7 is identical to 7 + x.
- (7 + x): Parentheses are often used for grouping terms, particularly when dealing with more complex expressions. In this case, the parentheses don't change the value of the expression.
Evaluating the Expression with Specific Values of x
To understand the expression's practical application, let's evaluate it using various values of x:
- If x = 3: 7 + x = 7 + 3 = 10
- If x = -5: 7 + x = 7 + (-5) = 2
- If x = 0: 7 + x = 7 + 0 = 7
- If x = 1/2: 7 + x = 7 + 1/2 = 14/2 + 1/2 = 15/2 = 7.5
- If x = π: 7 + x = 7 + π (approximately 7 + 3.14159 = 10.14159)
These examples illustrate how the value of the expression changes as we change the value of x. This adaptability is what makes algebraic expressions so powerful in representing real-world situations.
Applications of the Sum of 7 and x
The seemingly simple expression, 7 + x, has broad applications in numerous fields:
- Physics: Imagine calculating the total distance traveled. If an object initially travels 7 meters and then travels an additional 'x' meters, the total distance is 7 + x meters.
- Finance: Consider a scenario where you have $7 and earn an additional 'x' dollars. Your total money is represented by 7 + x dollars.
- Computer Science: In programming, this expression could represent the sum of a fixed value (7) and a dynamic value (x) obtained from user input or a calculation.
- Everyday Life: You bake 7 cookies, and your friend bakes x more. The total number of cookies is 7 + x.
These are just a few examples demonstrating the versatility of this fundamental expression. Its applicability extends to any situation where a constant value is added to a variable quantity.
Solving Equations Involving the Sum of 7 and x
Let's move beyond simply evaluating the expression and explore how it's used in solving equations. A common scenario involves setting the expression equal to a specific value and then solving for 'x'.
For instance:
7 + x = 12
To solve for x, we need to isolate 'x' on one side of the equation. We can do this by subtracting 7 from both sides:
7 + x - 7 = 12 - 7
x = 5
Therefore, if the sum of 7 and x is 12, then x must equal 5.
Here's another example:
7 + x = -3
Subtracting 7 from both sides:
7 + x - 7 = -3 - 7
x = -10
These examples demonstrate a fundamental algebraic operation: solving for an unknown variable. The ability to isolate and solve for 'x' is a cornerstone of algebra and opens the door to tackling more complex equations.
Expanding to More Complex Expressions
The sum of 7 and x can be part of a much larger and more complex algebraic expression. For example:
(7 + x) * 2 + 5
To evaluate this expression, we would first calculate the value inside the parentheses (7 + x), then multiply the result by 2, and finally add 5. The order of operations (PEMDAS/BODMAS) is crucial when dealing with such expressions.
Graphical Representation
We can graphically represent the sum of 7 and x using a Cartesian coordinate system. The expression 7 + x can be plotted as a straight line with a slope of 1 and a y-intercept of 7. Every point on this line represents a pair of values (x, y) where y = 7 + x.
Frequently Asked Questions (FAQ)
Q: What if x is a complex number?
A: The expression 7 + x still holds true even if x is a complex number (a number with a real and an imaginary part, represented as a + bi, where 'i' is the imaginary unit). The addition would follow the rules of complex number arithmetic.
Q: Can x be an irrational number?
A: Yes, x can be any real number, including irrational numbers like π (pi) or √2 (the square root of 2). The sum will still be valid, although the result might be an irrational number itself.
Q: Is there a limit to the value of x?
A: No, x can take on any value within the set of real numbers (or complex numbers if you're working with complex numbers). There is no upper or lower bound.
Q: What is the difference between 7 + x and 7x?
A: 7 + x represents the sum of 7 and x, whereas 7x represents the product of 7 and x. The '+' symbol indicates addition, while the implicit multiplication between 7 and x in 7x is implied. These are fundamentally different operations.
Conclusion: The Significance of a Simple Expression
The seemingly simple expression "the sum of 7 and x" serves as a powerful introduction to the world of algebra. By understanding this expression, we grasp the fundamental concepts of variables, constants, algebraic manipulation, and equation solving. Its wide range of applications across various fields underscores its importance as a building block for more complex mathematical concepts. While its initial appearance may seem basic, the underlying principles and its practical implications are profound, making it a cornerstone of mathematical literacy. Mastering this foundational concept is crucial for further advancement in mathematics and its diverse applications.
Latest Posts
Latest Posts
-
Grandma Made 1 5 Times As Many Pancakes And Waffles
Sep 14, 2025
-
A Solution With A Ph Of 2 Is
Sep 14, 2025
-
Track And Field Coaching Near Me
Sep 14, 2025
-
Find Parametric Equations For The Line Through
Sep 14, 2025
-
Which Graph Represents The Solution Set Of The Inequality
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about The Sum Of 7 And X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.