The Poh Of A 0.300 M Solution Of Naoh Is
faraar
Aug 28, 2025 · 6 min read
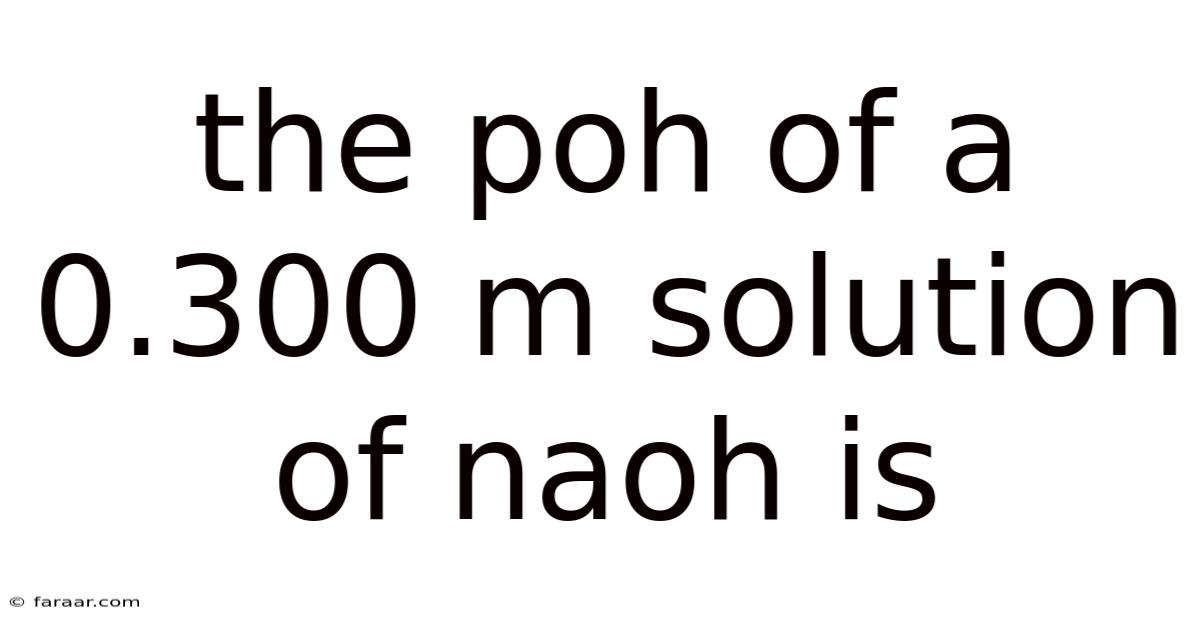
Table of Contents
The pH of a 0.300 M Solution of NaOH: A Deep Dive into Acid-Base Chemistry
Understanding pH is crucial in various fields, from chemistry and biology to environmental science and medicine. This article will explore how to calculate the pH of a 0.300 M solution of NaOH, a strong base, providing a comprehensive explanation suitable for students and anyone interested in learning more about acid-base chemistry. We will delve into the concepts of strong bases, the relationship between pOH and pH, and the importance of understanding these concepts in practical applications. This detailed explanation will cover the necessary calculations and provide insight into the underlying principles.
Introduction to pH and pOH
The pH scale is a logarithmic scale used to specify the acidity or basicity (alkalinity) of an aqueous solution. It ranges from 0 to 14, with 7 being neutral. Solutions with a pH less than 7 are acidic, while solutions with a pH greater than 7 are basic or alkaline. The pH scale is based on the concentration of hydrogen ions (H⁺) in the solution. The lower the pH, the higher the concentration of H⁺ ions.
However, when dealing with basic solutions, it's often more convenient to work with pOH, which is the negative logarithm (base 10) of the hydroxide ion (OH⁻) concentration:
pOH = -log₁₀[OH⁻]
The relationship between pH and pOH is given by:
pH + pOH = 14 (at 25°C)
This equation holds true for aqueous solutions at standard temperature (25°C). This is because the product of the concentrations of H⁺ and OH⁻ ions is always constant (Kw = [H⁺][OH⁻] = 1.0 x 10⁻¹⁴ at 25°C). This constant, Kw, is known as the ion product constant of water.
NaOH: A Strong Base
Sodium hydroxide (NaOH), also known as lye or caustic soda, is a strong base. This means it completely dissociates in water, meaning every molecule of NaOH breaks apart into its constituent ions (Na⁺ and OH⁻). This complete dissociation is key to calculating the pH (or pOH) of the solution. The equation representing this dissociation is:
NaOH(aq) → Na⁺(aq) + OH⁻(aq)
This complete dissociation simplifies the calculation significantly, unlike weak bases which only partially dissociate.
Calculating the pOH of a 0.300 M NaOH Solution
Since NaOH is a strong base and completely dissociates, the concentration of OH⁻ ions is equal to the concentration of the NaOH solution. Therefore, in a 0.300 M NaOH solution:
[OH⁻] = 0.300 M
Now, we can calculate the pOH using the formula:
pOH = -log₁₀[OH⁻] = -log₁₀(0.300)
Using a calculator, we find:
pOH ≈ 0.523
Calculating the pH of a 0.300 M NaOH Solution
Now that we have the pOH, we can easily calculate the pH using the relationship:
pH + pOH = 14
Therefore:
pH = 14 - pOH = 14 - 0.523 ≈ 13.477
Therefore, the pH of a 0.300 M solution of NaOH is approximately 13.48. This high pH value confirms that the solution is strongly basic.
Understanding the Significance of pH Calculations
Calculating the pH of solutions is essential in numerous applications:
- Chemistry: Precise pH control is critical in many chemical reactions and processes, ensuring the desired outcome and preventing unwanted side reactions.
- Biology: Maintaining the correct pH is vital for biological systems. Enzymes, for example, function optimally within a specific pH range. Changes in pH can affect the structure and activity of these enzymes.
- Environmental Science: Monitoring and controlling pH in water bodies is crucial for maintaining the health of aquatic ecosystems. Acid rain, for instance, can drastically lower the pH of lakes and rivers, harming aquatic life.
- Medicine: pH plays a vital role in many physiological processes in the human body. Maintaining the correct blood pH is crucial for survival. Changes in blood pH can indicate medical conditions.
- Agriculture: Soil pH affects nutrient availability to plants. Farmers often monitor and adjust soil pH to ensure optimal plant growth.
Factors Affecting pH Measurements
While the calculation above provides a good approximation, several factors can influence the accuracy of pH measurements in real-world scenarios:
- Temperature: The ion product constant of water (Kw) varies with temperature. The equation pH + pOH = 14 is only strictly true at 25°C. At higher temperatures, Kw increases, affecting both pH and pOH values.
- Ionic Strength: The presence of other ions in the solution can affect the activity of the hydroxide ions, altering the measured pH. This is because ions can interact with each other, affecting their effective concentrations.
- Activity Coefficients: These coefficients account for the deviations from ideal behavior in solutions with high ionic strengths. They are used to correct the calculated pH for the non-ideal behavior of ions.
- Accuracy of Measurement Tools: The accuracy of pH meters and other measurement tools plays a crucial role in obtaining precise pH values. Calibration and proper usage are essential.
Frequently Asked Questions (FAQ)
Q: What is the difference between a strong base and a weak base?
A: A strong base completely dissociates into its ions in water, while a weak base only partially dissociates. This difference significantly impacts the pH calculation because a strong base directly contributes the full concentration of hydroxide ions, whereas a weak base requires considering the equilibrium constant (Kb) for calculation.
Q: Can pH be negative?
A: Yes, although rare, pH can be negative. This occurs in highly concentrated solutions of strong acids where the concentration of hydrogen ions is extremely high.
Q: How is pH measured?
A: pH is typically measured using a pH meter, a device with a special electrode that senses the hydrogen ion concentration. Alternatively, pH indicators (like litmus paper) can provide a less precise estimation.
Q: What is the significance of the ion product constant of water (Kw)?
A: Kw represents the equilibrium constant for the autoionization of water (2H₂O ⇌ H₃O⁺ + OH⁻). It is crucial in relating pH and pOH, as it defines the relationship between hydrogen and hydroxide ion concentrations in aqueous solutions.
Conclusion
Calculating the pH of a 0.300 M NaOH solution involves understanding the concept of strong bases, their complete dissociation in water, and the relationship between pH and pOH. The calculation demonstrates that a 0.300 M NaOH solution has a pH of approximately 13.48, indicating a strongly basic solution. Understanding pH calculations is essential across various scientific disciplines, highlighting the importance of mastering these fundamental concepts in acid-base chemistry. While this calculation provides a good approximation, it's important to consider factors like temperature and ionic strength for more accurate measurements in real-world applications. The detailed explanation provided here aims to equip readers with a deeper understanding of pH and its significance beyond the simple calculation itself.
Latest Posts
Latest Posts
-
Guitar Lessons In Boca Raton Fl
Aug 28, 2025
-
Is The Limiting Reactant The Theoretical Yield
Aug 28, 2025
-
A Quadrilateral With 2 Acute Angles
Aug 28, 2025
-
Nuclear Symbol For Br With 46 Neutrons
Aug 28, 2025
-
How Many 2 3 Cups Are In 4 Cups
Aug 28, 2025
Related Post
Thank you for visiting our website which covers about The Poh Of A 0.300 M Solution Of Naoh Is . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.