Square Root Of X To The 4th Power
faraar
Sep 13, 2025 · 5 min read
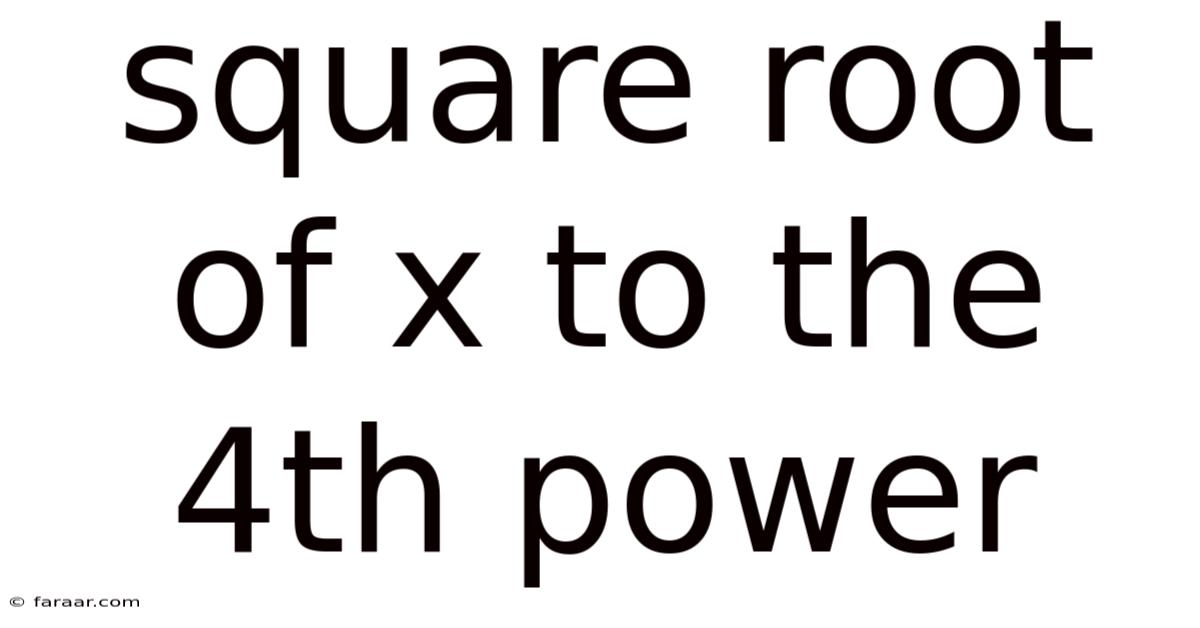
Table of Contents
Understanding the Square Root of x to the 4th Power: A Comprehensive Guide
The expression √(x⁴) – or the square root of x to the fourth power – might seem intimidating at first glance, but it's a concept readily understood with a little explanation. This article will delve into the intricacies of this mathematical expression, exploring its simplification, its implications in various fields, and addressing common queries. We'll break down the concept step-by-step, ensuring a comprehensive understanding, regardless of your current mathematical background. This will cover everything from the basic principles to more advanced applications, making it a valuable resource for students, educators, and anyone curious about the subject.
Introduction: What is √(x⁴)?
At its core, √(x⁴) represents the principal square root of x raised to the power of four. The square root operation (√) finds a number that, when multiplied by itself, equals the number under the radical sign. In this case, we're looking for a number that, when squared, results in x⁴. Understanding this fundamental concept is crucial before delving into the simplification and applications. The key lies in the properties of exponents and how they interact with the square root operation.
Simplifying √(x⁴)
The simplification process hinges on the understanding of exponent rules. Recall that the square root of a number is equivalent to raising that number to the power of 1/2. Therefore, we can rewrite √(x⁴) as (x⁴)^(1/2). Using the power of a power rule – which states that (aᵐ)ⁿ = aᵐⁿ – we can simplify this expression:
(x⁴)^(1/2) = x⁴⁽¹/²⁾ = x²
Therefore, the simplified form of √(x⁴) is x². This simplification holds true for all positive values of x. However, when dealing with negative values of x, the situation becomes slightly more nuanced, as we will explore further below.
The Importance of Absolute Value
While x² is the simplified form for positive x, it's vital to consider the case when x is negative. Let's examine why the absolute value becomes relevant.
Consider the case where x = -2. Then x⁴ = (-2)⁴ = 16. The square root of 16 is 4. However, if we simply substitute x = -2 into the simplified expression x², we get (-2)² = 4, which is correct. Now let's try x = -3. x⁴ = (-3)⁴ = 81, and √81 = 9. Again, substituting into x² gives (-3)² = 9, which is also correct.
It seems that x² works fine even for negative x. However, let's consider the general case. We know that the square root operation always yields a non-negative result (or a complex number if we are working with the complex numbers). If we had simply used x², and substituted a negative value of x, we’d get a positive number as the result, fulfilling this requirement.
Therefore, for all real values of x, the most accurate representation of √(x⁴) is |x²|. While x² will usually give the correct numerical answer, using the absolute value ensures mathematical rigor and accuracy, especially when dealing with further mathematical manipulations or proofs. The absolute value guarantees a non-negative result, consistent with the definition of the square root function in the real numbers.
Extending the Concept: Higher Powers and Roots
The principles discussed above can be extended to higher powers and roots. For example, consider the cube root of x to the sixth power: ∛(x⁶). This can be rewritten as (x⁶)^(1/3) = x⁶⁽¹/³⁾ = x². Notice that we don't need absolute value signs here because the cube root of a number can be negative. This highlights the importance of considering the specific exponent and root involved when simplifying such expressions. The even powers interacting with even roots require absolute values for complete mathematical accuracy.
Applications of √(x⁴) and Related Concepts
The concept of simplifying expressions involving roots and powers has vast applications across numerous fields. Some examples include:
-
Calculus: Derivatives and integrals frequently involve expressions with roots and powers. Simplifying these expressions before performing calculus operations often simplifies the calculation and provides a more elegant solution.
-
Physics: Many physics equations, particularly those concerning motion, energy, and forces, utilize powers and roots in their formulation. Simplifying expressions can provide a clearer understanding of the underlying physical relationships.
-
Engineering: In various engineering disciplines, calculating stress, strain, and other parameters often involves simplifying expressions containing powers and roots.
-
Computer Science: Algorithms and data structures sometimes require optimizing expressions involving powers and roots for efficient processing.
-
Financial Mathematics: Compound interest calculations frequently use exponential functions, and simplifying related expressions is crucial for accurate calculations.
Frequently Asked Questions (FAQ)
Here are some frequently asked questions regarding the square root of x to the fourth power:
-
Q: Is √(x⁴) always equal to x²?
A: While it's numerically equal for many common cases, the mathematically precise and rigorously correct answer is |x²|. This guarantees a non-negative result, consistent with the definition of the principal square root.
-
Q: What happens if x is a complex number?
A: When dealing with complex numbers, the concept of a principal square root becomes more intricate. The square root of a complex number is not a single value but involves multiple branches. In the case of √(x⁴), where x is complex, the result would be a multi-valued function.
-
Q: Can I simplify √(x⁴ + y⁴)?
A: No, there's no general simplification for √(x⁴ + y⁴). It cannot be reduced to a simpler form using elementary mathematical operations.
Conclusion: A Deeper Understanding
Understanding the square root of x to the fourth power goes beyond simple calculation. It requires a solid grasp of exponent rules and the implications of absolute values. While x² might seem like a sufficient simplification for many practical applications, the use of |x²| guarantees mathematical precision and avoids potential ambiguities, particularly when working with negative values of x. The principles discussed here extend to other expressions involving higher powers and roots, underscoring the importance of mastering these fundamental concepts. Through this comprehensive guide, we hope we've clarified the intricacies and applications of this important mathematical expression. By understanding the nuances surrounding this seemingly simple expression, you build a strong foundation for more advanced mathematical concepts and problem-solving. The key lies in understanding the underlying rules and principles, allowing for elegant and accurate solutions across various fields.
Latest Posts
Latest Posts
-
Which Best Explains Why Water Has A High Specific Heat
Sep 14, 2025
-
What Is A Positive Divided By Negative
Sep 14, 2025
-
How Many Moles Of Water Are Produced In This Reaction
Sep 14, 2025
-
Weight Of A Pencil In Grams
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of X To The 4th Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.