Solve For . Give An Exact Answer.
faraar
Sep 21, 2025 · 5 min read
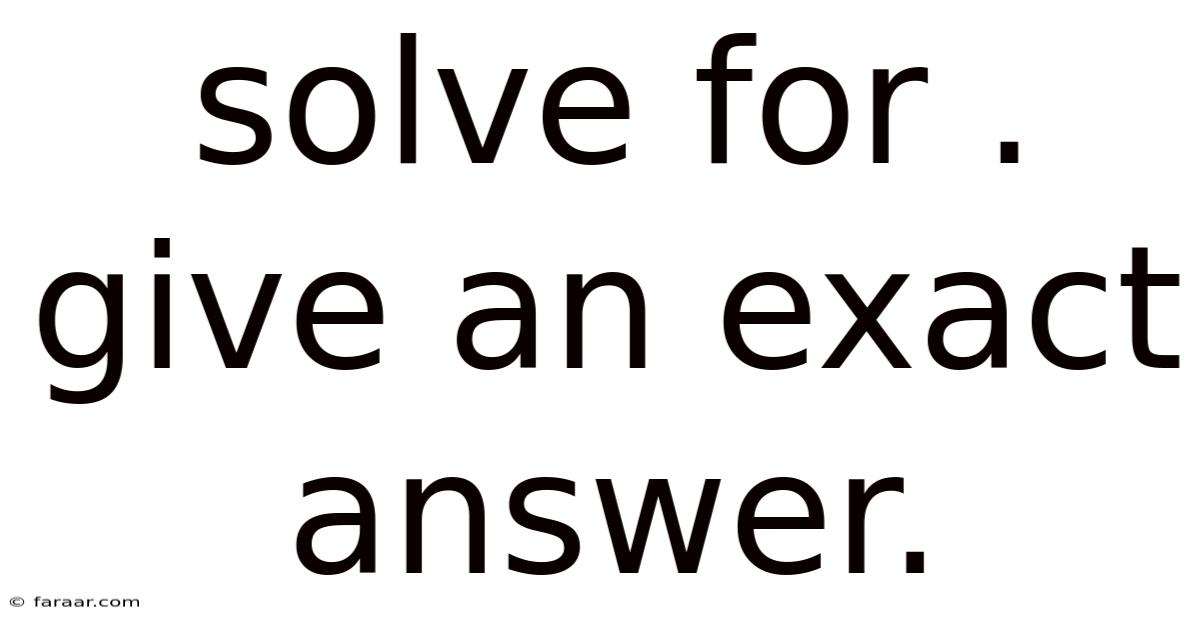
Table of Contents
Solving for x: A Comprehensive Guide to Finding Exact Answers
Finding the value of an unknown variable, often represented by 'x', is a fundamental concept in mathematics. This article provides a comprehensive guide on how to solve for x, covering various methods and scenarios, with a focus on achieving exact answers. We'll delve into different types of equations, from simple linear equations to more complex quadratic and exponential equations, providing clear explanations and worked examples. Mastering these techniques is crucial for success in algebra and beyond, forming the bedrock for more advanced mathematical concepts.
Understanding the Basics: Linear Equations
The simplest type of equation to solve for x is a linear equation. A linear equation is an equation where the highest power of the variable (x) is 1. These equations generally follow the form: ax + b = c, where 'a', 'b', and 'c' are constants.
Solving a Linear Equation: The goal is to isolate 'x' on one side of the equation. This is done by performing inverse operations.
Example 1: Solve for x: 3x + 5 = 14
- Subtract 5 from both sides: 3x + 5 - 5 = 14 - 5 => 3x = 9
- Divide both sides by 3: 3x / 3 = 9 / 3 => x = 3
Therefore, the exact solution for x is 3.
Example 2: Solve for x: 2x - 7 = 11
- Add 7 to both sides: 2x - 7 + 7 = 11 + 7 => 2x = 18
- Divide both sides by 2: 2x / 2 = 18 / 2 => x = 9
The exact solution for x is 9.
Example 3 (with fractions): Solve for x: (1/2)x + 3 = 7
- Subtract 3 from both sides: (1/2)x + 3 - 3 = 7 - 3 => (1/2)x = 4
- Multiply both sides by 2: 2 * (1/2)x = 4 * 2 => x = 8
The exact solution for x is 8.
Example 4 (with decimals): Solve for x: 0.5x - 2.5 = 1.5
- Add 2.5 to both sides: 0.5x - 2.5 + 2.5 = 1.5 + 2.5 => 0.5x = 4
- Divide both sides by 0.5: 0.5x / 0.5 = 4 / 0.5 => x = 8
The exact solution for x is 8. Note that working with decimals can sometimes lead to rounding errors, so it's often beneficial to convert decimals to fractions whenever possible for greater accuracy.
Solving for x in More Complex Equations
Linear equations are straightforward, but many problems involve more complex equations. Let's explore some of these:
Quadratic Equations
Quadratic equations have the general form: ax² + bx + c = 0, where a, b, and c are constants and a ≠ 0. Solving these often requires factoring, using the quadratic formula, or completing the square.
Factoring: This method involves expressing the quadratic as a product of two linear expressions.
Example 5: Solve for x: x² + 5x + 6 = 0
This equation factors to (x + 2)(x + 3) = 0. Therefore, x = -2 or x = -3.
Quadratic Formula: The quadratic formula provides a direct solution for x:
x = [-b ± √(b² - 4ac)] / 2a
Example 6: Solve for x: 2x² - 5x + 2 = 0
Here, a = 2, b = -5, and c = 2. Plugging these values into the quadratic formula:
x = [5 ± √((-5)² - 4 * 2 * 2)] / (2 * 2) = [5 ± √9] / 4 = [5 ± 3] / 4
Therefore, x = 2 or x = 1/2.
Exponential Equations
Exponential equations involve variables in the exponent. Solving these often requires using logarithms.
Example 7: Solve for x: 2ˣ = 16
We can rewrite 16 as 2⁴, so the equation becomes: 2ˣ = 2⁴. Therefore, x = 4.
Example 8: Solve for x: 3ˣ = 27
We can rewrite 27 as 3³, so the equation becomes: 3ˣ = 3³. Therefore, x = 3.
Example 9 (requiring logarithms): Solve for x: eˣ = 10
Taking the natural logarithm (ln) of both sides: ln(eˣ) = ln(10) => x = ln(10). This is the exact answer; a numerical approximation can be obtained using a calculator.
Systems of Equations
Sometimes, you need to solve for x within a system of equations. This usually involves methods like substitution or elimination.
Example 10 (Substitution):
- x + y = 5
- 2x - y = 1
From the first equation, we can express y as y = 5 - x. Substituting this into the second equation:
2x - (5 - x) = 1 => 3x - 5 = 1 => 3x = 6 => x = 2
Substituting x = 2 back into y = 5 - x gives y = 3. Thus, the solution is x = 2, y = 3.
Example 11 (Elimination):
- 3x + 2y = 7
- x - 2y = 1
Adding the two equations eliminates y: 4x = 8 => x = 2. Substituting x = 2 into either of the original equations gives y = 5/4.
Handling Absolute Value Equations
Equations involving absolute values require careful consideration of both positive and negative cases.
Example 12: Solve for x: |x - 2| = 5
This means either x - 2 = 5 or x - 2 = -5. Solving these gives x = 7 or x = -3.
Dealing with Inequalities
Solving for x in inequalities involves similar techniques to solving equations, but with additional considerations regarding the inequality signs.
Example 13: Solve for x: 2x + 3 > 7
- Subtract 3 from both sides: 2x > 4
- Divide by 2: x > 2
Common Mistakes to Avoid
- Incorrect order of operations: Always follow the order of operations (PEMDAS/BODMAS).
- Errors in manipulating equations: Remember to perform the same operation on both sides of the equation.
- Forgetting to consider all possible solutions: Especially relevant for quadratic equations and absolute value equations.
- Rounding errors: Avoid rounding intermediate results, particularly when dealing with decimals and fractions. Aim for exact answers whenever possible.
Conclusion
Solving for x is a fundamental skill in mathematics. By mastering the techniques outlined above—including those for linear, quadratic, and exponential equations, along with systems of equations and absolute value equations—you’ll build a strong foundation for more advanced mathematical concepts. Remember to practice regularly, focusing on understanding the underlying principles rather than just memorizing formulas. With consistent effort and attention to detail, you can confidently solve for x and achieve exact answers in a wide variety of mathematical problems. The key is to break down complex problems into smaller, manageable steps, always double-checking your work for accuracy.
Latest Posts
Latest Posts
-
Is The Autoionization Of Water Exothermic Or Endothermic
Sep 22, 2025
-
Algebra 2 Common Core Homework Answers
Sep 22, 2025
-
How To Find The Y Intercept From 2 Points
Sep 22, 2025
-
For Which Positive Integers K Is The Following Series Convergent
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Solve For . Give An Exact Answer. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.