Six More Than Three Times A Number W
faraar
Aug 27, 2025 · 5 min read
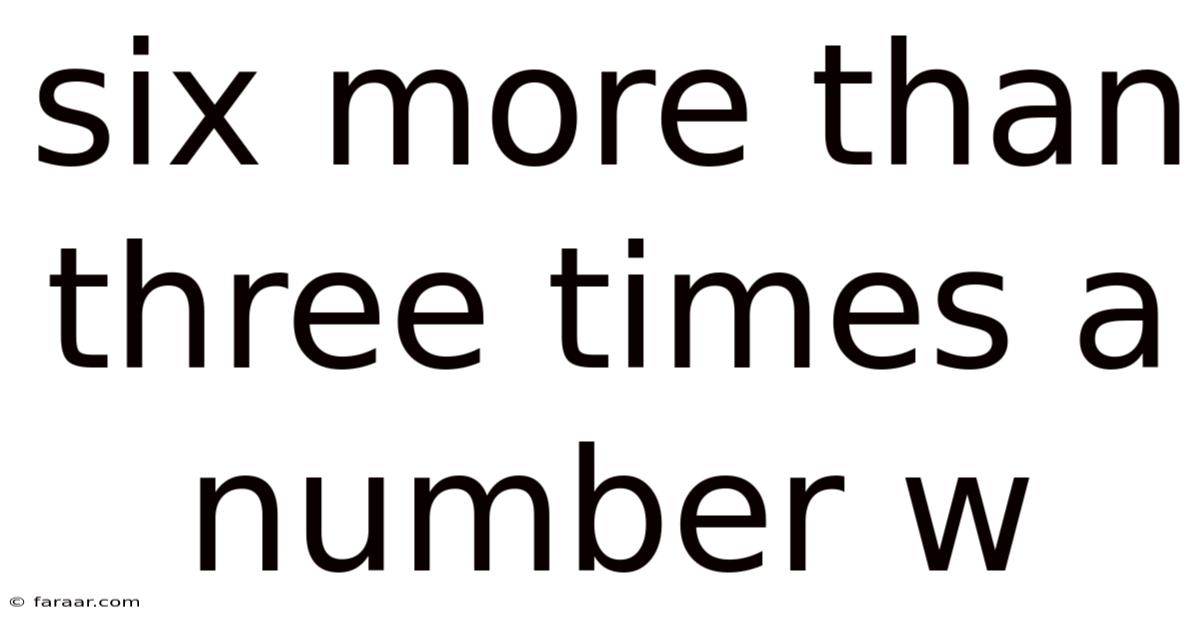
Table of Contents
Six More Than Three Times a Number: Unraveling the Math Behind the Phrase
This article delves into the mathematical expression "six more than three times a number," exploring its translation into algebraic notation, solving related equations, and extending the concept to more complex scenarios. We will cover various methods for solving these types of problems, including practical examples and frequently asked questions. Understanding this seemingly simple phrase unlocks a fundamental skill in algebra and lays the groundwork for more advanced mathematical concepts.
Introduction: From Words to Equations
The phrase "six more than three times a number" might seem intimidating at first glance, but it's a straightforward representation of an algebraic expression. The key to understanding it lies in breaking it down step by step. Let's analyze each component:
- A number: This represents an unknown value, typically denoted by a variable like x, y, or n.
- Three times a number: This translates to 3 multiplied by the number, or 3*x (if we use x as our variable).
- Six more than: This indicates adding 6 to the previous result.
Therefore, the complete algebraic expression for "six more than three times a number" is 3x + 6. This simple equation forms the basis for numerous mathematical problems.
Solving Equations Involving "Six More Than Three Times a Number"
Now that we have the algebraic representation, let's explore how to solve equations involving this expression. Different problems will present this phrase within a larger equation. Let's examine a few examples:
Example 1: Finding the Number
Problem: Six more than three times a number is 15. Find the number.
Solution:
- Translate the problem into an equation: "Six more than three times a number is 15" translates to 3x + 6 = 15.
- Isolate the variable: Subtract 6 from both sides of the equation: 3x = 9.
- Solve for x: Divide both sides by 3: x = 3.
Therefore, the number is 3. We can verify this by substituting x = 3 back into the original equation: 3(3) + 6 = 15, which is true.
Example 2: A More Complex Equation
Problem: Twice the quantity of six more than three times a number is equal to 30. Find the number.
Solution:
- Translate the problem: "Twice the quantity of six more than three times a number" translates to 2(3x + 6). The entire equation becomes 2(3x + 6) = 30.
- Distribute: Expand the parentheses: 6x + 12 = 30.
- Isolate the variable: Subtract 12 from both sides: 6x = 18.
- Solve for x: Divide both sides by 6: x = 3.
Again, the number is 3. This example demonstrates how the original expression can be embedded within a more complex equation.
Example 3: Working with Inequalities
Problem: Six more than three times a number is greater than or equal to 21. Find the possible values of the number.
Solution:
- Translate the problem into an inequality: This translates to 3x + 6 ≥ 21.
- Isolate the variable: Subtract 6 from both sides: 3x ≥ 15.
- Solve for x: Divide both sides by 3: x ≥ 5.
This means the number can be any value greater than or equal to 5.
Expanding the Concept: Variations and Applications
The basic expression "six more than three times a number" can be modified and applied in various ways. Let's consider some variations:
- Changing the constants: Instead of "six more," we could have "ten more," "five less," or any other constant. The core principle of translating words into algebraic expressions remains the same.
- Multiple variables: We could introduce another variable, creating an equation like "six more than three times a number plus twice another number equals 20." This would involve solving a system of equations.
- Word problems: Many word problems in algebra utilize this type of phrasing to describe real-world scenarios involving unknown quantities. For example, a problem might involve the cost of items, distances, or time.
The Scientific Explanation: Why this Matters
The ability to translate word problems into algebraic expressions is fundamental to algebra and beyond. This skill underpins the ability to model real-world situations mathematically, solve problems using logical reasoning, and develop critical thinking skills. This concept isn't just about manipulating numbers; it's about developing the ability to abstract and represent relationships using mathematical symbols. This skill is crucial for fields like:
- Engineering: Designing structures, calculating forces, and predicting behavior.
- Physics: Formulating and solving equations that describe physical phenomena.
- Computer Science: Developing algorithms and writing code that can solve complex problems.
- Economics: Modeling economic systems and predicting market trends.
Moreover, the systematic approach of breaking down complex sentences into smaller, manageable components teaches valuable problem-solving strategies applicable in various aspects of life.
Frequently Asked Questions (FAQs)
-
Q: What if the phrase is "three times a number plus six"? A: This is equivalent to "six more than three times a number" and is expressed algebraically as 3x + 6. The order of addition doesn't affect the result.
-
Q: How do I deal with negative numbers in these types of problems? A: Negative numbers are handled the same way as positive numbers, following the rules of algebra. For example, if the problem were "six less than three times a number," the equation would be 3x - 6.
-
Q: What if the problem involves fractions or decimals? A: Fractions and decimals are handled using the standard rules of arithmetic and algebra. You’ll use the same steps to solve the equation, just with fractions or decimals instead of whole numbers.
-
Q: Can this concept be applied to more than one unknown variable? A: Yes, absolutely. You would need to create a system of equations to solve for multiple unknown variables. For example: "Three times one number plus six more than a second number equals 25, and the sum of the two numbers is 10." This would require solving two simultaneous equations.
Conclusion: Mastering the Fundamentals
Understanding the expression "six more than three times a number" and its algebraic representation is a cornerstone of elementary algebra. By mastering this seemingly simple phrase, you unlock a powerful tool for solving a vast range of mathematical problems and build a solid foundation for more advanced mathematical concepts. The ability to translate words into mathematical symbols is not just about solving equations; it's about developing critical thinking skills and a powerful approach to problem-solving that will benefit you far beyond the classroom. The key lies in consistent practice, breaking down complex problems into smaller steps, and appreciating the interconnectedness of mathematical concepts.
Latest Posts
Latest Posts
-
The Product Of 7 And The Square Of A Number
Aug 28, 2025
-
Is The Nclex The Same In Every State
Aug 28, 2025
-
A Diprotic Acid H2a Has Ka1
Aug 28, 2025
-
Does Distributive Property Come Before Pemdas
Aug 28, 2025
-
How To Determine Whether The Sequence Converges Or Diverges
Aug 28, 2025
Related Post
Thank you for visiting our website which covers about Six More Than Three Times A Number W . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.