Sin X 1 3 Find Cos X
faraar
Sep 23, 2025 · 5 min read
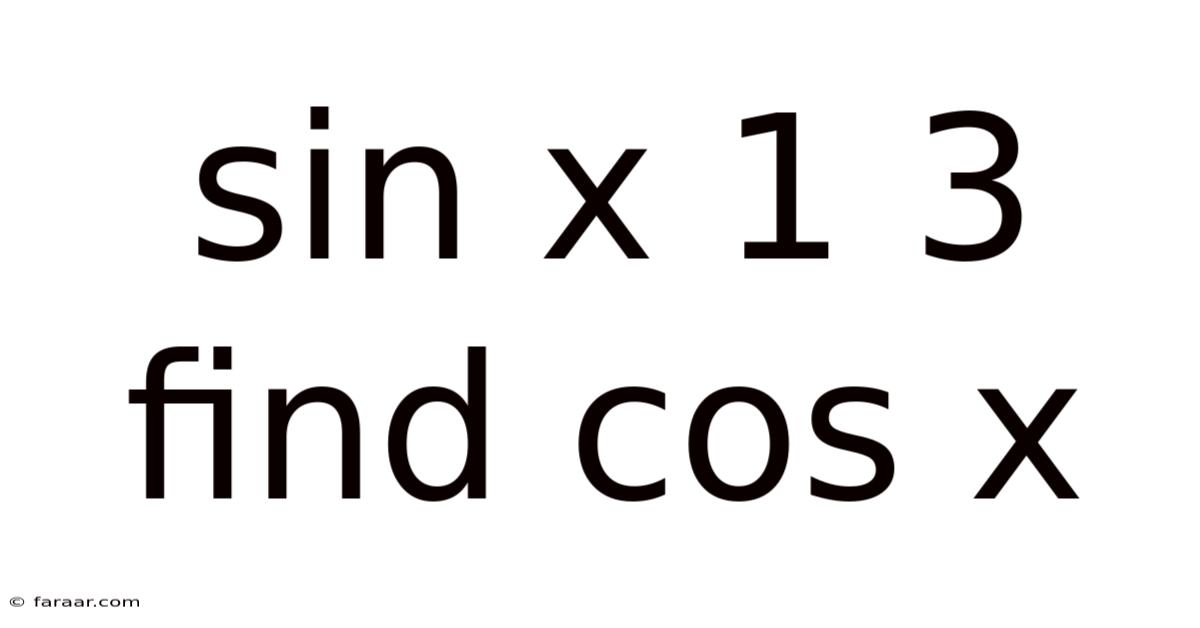
Table of Contents
Finding cos x when sin x = 1/3: A Comprehensive Guide
Determining the value of cos x when given sin x = 1/3 might seem straightforward at first glance, but it requires a nuanced understanding of trigonometric identities and the concept of multiple solutions within a trigonometric function's range. This article will delve into the problem, exploring various approaches and highlighting potential pitfalls. We'll cover the fundamental trigonometric identity, the use of the unit circle, the importance of considering the quadrant, and address frequently asked questions to provide a complete and accessible guide.
Introduction: The Power of Trigonometric Identities
The core of solving this problem lies in the fundamental trigonometric identity: sin²x + cos²x = 1. This equation holds true for all values of x, making it a powerful tool in manipulating trigonometric expressions. Given that sin x = 1/3, we can substitute this value into the identity to solve for cos x. However, the process is not as simple as direct substitution, as we will see. We'll also explore how to visualize this relationship using the unit circle. Understanding these concepts is crucial for mastering trigonometry and solving more complex problems.
Step-by-Step Solution: Utilizing the Fundamental Identity
-
Substitute the known value: We begin with the fundamental identity: sin²x + cos²x = 1. We know that sin x = 1/3, so we substitute this value: (1/3)² + cos²x = 1.
-
Simplify the equation: This simplifies to 1/9 + cos²x = 1.
-
Isolate cos²x: Subtracting 1/9 from both sides gives cos²x = 1 - 1/9 = 8/9.
-
Solve for cos x: Taking the square root of both sides, we get cos x = ±√(8/9) = ±(2√2)/3.
The Crucial Role of Quadrants: Multiple Solutions
Notice the ± sign in our solution for cos x. This highlights a critical point: there are two possible values for cos x. The sign of cos x depends entirely on the quadrant in which the angle x lies.
-
Quadrant I (0° < x < 90°): In this quadrant, both sine and cosine are positive. Therefore, if x is in Quadrant I, cos x = (2√2)/3.
-
Quadrant II (90° < x < 180°): In this quadrant, sine is positive and cosine is negative. Therefore, if x is in Quadrant II, cos x = -(2√2)/3.
-
Quadrants III and IV: Sine is negative in Quadrants III and IV, making it impossible for sin x to equal 1/3 in these quadrants.
Visualizing with the Unit Circle
The unit circle provides a powerful visual representation of this problem. The sine of an angle is the y-coordinate of the point where the terminal side of the angle intersects the unit circle. The cosine is the x-coordinate. If sin x = 1/3, we're looking for points on the unit circle with a y-coordinate of 1/3. There are two such points, one in Quadrant I and one in Quadrant II, each with a different x-coordinate (cosine value).
Further Exploration: Inverse Trigonometric Functions
While the fundamental identity provides a direct solution, we can also utilize inverse trigonometric functions. We can find a reference angle using the arcsine function:
x_ref = arcsin(1/3)
This will give you the angle in Quadrant I. To find the angle in Quadrant II, you would subtract the reference angle from 180°. Remember to account for the periodic nature of trigonometric functions; there are infinitely many angles with a sine of 1/3.
Understanding the Limitations: Ambiguity and Context
The ambiguity in the solution (cos x = ±(2√2)/3) highlights a crucial point in trigonometry: a single trigonometric value (like sin x = 1/3) does not uniquely determine the angle x. Additional information, such as the range of x or the quadrant in which x lies, is necessary to obtain a unique solution.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this directly?
A: Yes, your calculator's arcsin function will give you the reference angle. However, remember to consider the quadrant to determine the correct sign for cos x.
-
Q: What if sin x was a negative value?
A: If sin x were negative, you would only consider Quadrants III and IV, where sine is negative. The procedure for solving for cos x remains the same, but the possible quadrants and thus the sign of cos x would change.
-
Q: How do I check my answer?
A: Substitute both possible values of cos x ((2√2)/3 and -(2√2)/3) back into the fundamental identity (sin²x + cos²x = 1) along with sin x = 1/3. Both should satisfy the equation.
-
Q: Are there any other trigonometric identities that could be used?
A: While the fundamental identity is the most direct approach, you could potentially use other identities, but they would likely lead to a more complex solution. The fundamental identity offers the most straightforward path.
Conclusion: Mastering the Nuances of Trigonometric Solutions
Solving for cos x given sin x = 1/3 requires a solid understanding of the fundamental trigonometric identity, the concept of quadrants, and the implications of multiple solutions. The problem highlights the importance of careful consideration of the context and the use of visual aids like the unit circle to grasp the geometric interpretation of trigonometric functions. By mastering these concepts, you'll be well-equipped to tackle more complex trigonometric problems and deepen your understanding of this crucial area of mathematics. Remember to always check your solutions and consider the possible quadrants to ensure accuracy. The ± sign in our solution is not a mere mathematical detail but a crucial indicator of the richness and complexity within trigonometric relationships.
Latest Posts
Latest Posts
-
The Quotient Of A Number And 4 Is 7
Sep 23, 2025
-
1 3 Cup Twice Is How Much
Sep 23, 2025
-
How Much Cashews At 1 58 Per Pound
Sep 23, 2025
-
Find X Such That The Matrix Is Singular
Sep 23, 2025
-
V E N I In English
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Sin X 1 3 Find Cos X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.