Lcm Of 5 6 And 7
faraar
Sep 09, 2025 · 5 min read
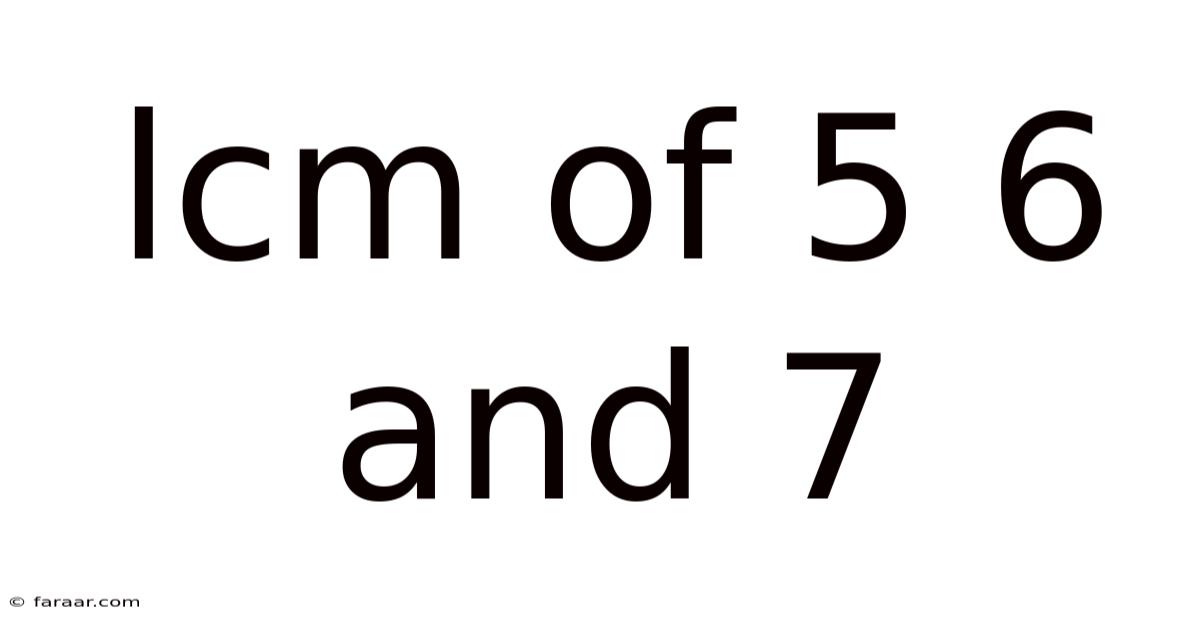
Table of Contents
Finding the LCM of 5, 6, and 7: A Comprehensive Guide
Finding the Least Common Multiple (LCM) of a set of numbers is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving problems involving cycles and timing. This article will provide a thorough understanding of how to find the LCM of 5, 6, and 7, exploring different methods and delving into the underlying mathematical principles. We'll also explore practical applications and address frequently asked questions. By the end, you’ll not only know the LCM of these three numbers but also possess a robust understanding of the concept applicable to any set of numbers.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 5, 6, and 7, let's define the term. The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder. This concept is incredibly useful in various mathematical operations and real-world scenarios.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all three.
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110, 115, 120...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96, 102, 108, 114, 120...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126, 133, 140, 147, 154, 161, 168, 175, 182, 189, 196, 203, 210...
By comparing the lists, we can see that the smallest number common to all three lists is 210. Therefore, the LCM of 5, 6, and 7 is 210. While this method works well for smaller numbers, it can become cumbersome and time-consuming for larger numbers.
Method 2: Prime Factorization
This is a more efficient and systematic method, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from these factors.
-
Find the prime factorization of each number:
- 5 = 5 (5 is a prime number)
- 6 = 2 x 3
- 7 = 7 (7 is a prime number)
-
Identify the highest power of each prime factor present:
- The prime factors are 2, 3, 5, and 7.
- The highest power of 2 is 2¹ = 2
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
- The highest power of 7 is 7¹ = 7
-
Multiply the highest powers together:
- LCM(5, 6, 7) = 2 x 3 x 5 x 7 = 210
Therefore, the LCM of 5, 6, and 7 is 210. This method is generally preferred for its efficiency and accuracy, especially when dealing with larger numbers or a greater number of integers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
This formula can be extended to more than two numbers, although the calculation becomes more complex. While we can use this method, it's generally less efficient than prime factorization for finding the LCM of multiple numbers directly. However, understanding the relationship between LCM and GCD is important for a deeper understanding of number theory.
Explanation of the Mathematical Principles
The success of the prime factorization method lies in the Fundamental Theorem of Arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers (ignoring the order). This unique representation allows us to systematically construct the LCM by taking the highest power of each prime factor present in the numbers. The LCM represents the smallest number that contains all the prime factors of the individual numbers with their highest powers.
Practical Applications of LCM
The concept of LCM has numerous real-world applications:
-
Scheduling: Imagine three buses arrive at a bus stop at intervals of 5, 6, and 7 minutes respectively. The LCM (210 minutes) helps determine when all three buses will arrive simultaneously again.
-
Fraction Operations: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial for finding a common denominator.
-
Cycling Problems: Consider three cyclists cycling on a circular track with lengths that are multiples of 5, 6, and 7 kilometers. The LCM helps determine when they will meet again at the starting point.
-
Gear Ratios: In mechanical engineering, the LCM is used to calculate gear ratios and synchronize the rotations of multiple gears.
Frequently Asked Questions (FAQ)
Q: Is the LCM always greater than the largest number in the set?
A: Yes, the LCM will always be greater than or equal to the largest number in the set. It can be equal if the largest number is a multiple of all the other numbers.
Q: Can the LCM of two numbers be equal to their product?
A: Yes, this occurs when the two numbers are coprime (their greatest common divisor is 1). For example, LCM(5,7) = 35 = 5 x 7.
Q: How do I find the LCM of more than three numbers?
A: You can extend the prime factorization method. Find the prime factorization of each number, identify the highest power of each prime factor present, and multiply these highest powers together.
Q: What if one of the numbers is zero?
A: The LCM is undefined if one of the numbers is zero. The LCM is only defined for positive integers.
Conclusion
Finding the LCM of 5, 6, and 7, whether through listing multiples, prime factorization, or understanding the relationship with the GCD, solidifies the understanding of a critical mathematical concept. The prime factorization method stands out for its efficiency and applicability to a wide range of numbers. Remember, the LCM is more than just a mathematical operation; it's a tool with significant practical applications in various fields. Mastering this concept enhances your problem-solving skills and provides a deeper appreciation for the elegance and interconnectedness of mathematics. The ability to calculate LCM efficiently, using methods appropriate to the situation, is a valuable skill for anyone pursuing further mathematical studies or applying mathematical principles in their chosen field.
Latest Posts
Latest Posts
-
What Is The Product Of 8 And 5
Sep 09, 2025
-
Find The Function R That Satisfies The Following Conditions
Sep 09, 2025
-
Find The Molar Mass Of Ethanol C2h6o
Sep 09, 2025
-
How To Find A 90 Confidence Interval
Sep 09, 2025
-
An Integer Which Is Not A Whole Number
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 5 6 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.