Is 5 6 Greater Than 3 4
faraar
Aug 26, 2025 · 5 min read
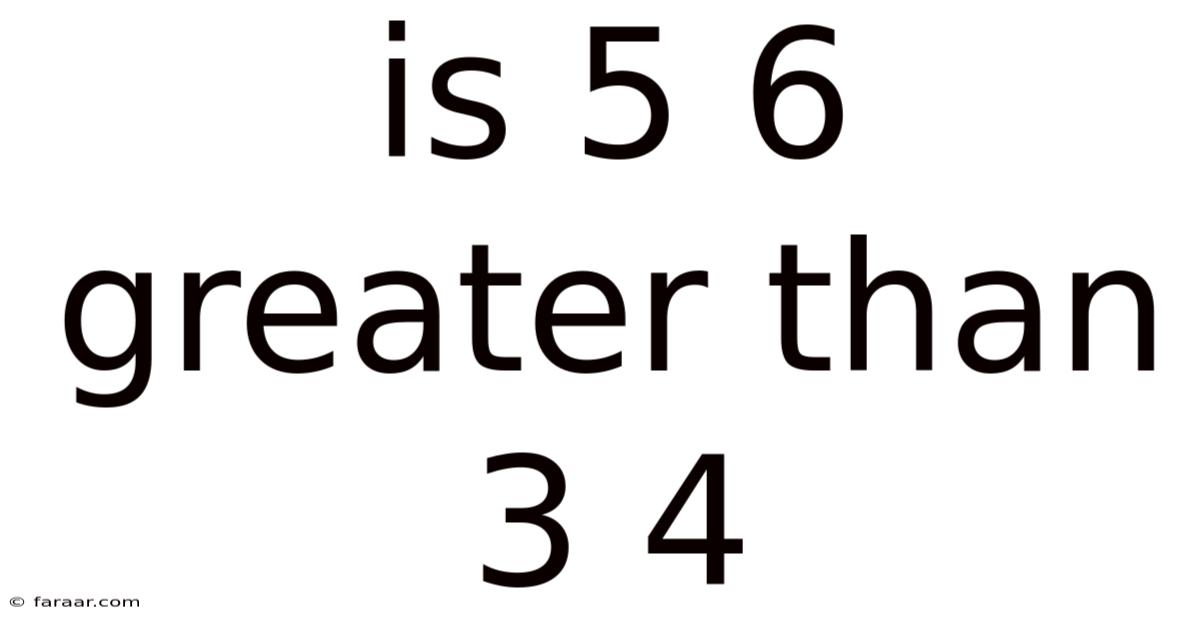
Table of Contents
Is 5/6 Greater Than 3/4? A Deep Dive into Fraction Comparison
Determining whether 5/6 is greater than 3/4 might seem like a simple question, especially for those comfortable with fractions. However, understanding the underlying principles of fraction comparison is crucial for building a strong foundation in mathematics. This article will not only answer the question definitively but also explore various methods for comparing fractions, providing a comprehensive understanding that extends beyond this specific example. We'll delve into the practical applications and the underlying mathematical reasoning, ensuring a thorough grasp of the concept.
Understanding Fractions: A Quick Refresher
Before jumping into the comparison, let's quickly recap what fractions represent. A fraction, like 5/6, represents a part of a whole. The number on top (5) is called the numerator, representing the number of parts we have. The number on the bottom (6) is called the denominator, representing the total number of equal parts the whole is divided into. Therefore, 5/6 signifies that we have 5 out of 6 equal parts of a whole. Similarly, 3/4 means we have 3 out of 4 equal parts.
Method 1: Finding a Common Denominator
The most straightforward method for comparing fractions is to find a common denominator. This means finding a number that is a multiple of both denominators (6 and 4 in this case). The least common multiple (LCM) of 6 and 4 is 12.
-
Convert 5/6: To get a denominator of 12, we multiply both the numerator and denominator of 5/6 by 2: (5 x 2) / (6 x 2) = 10/12. Remember, multiplying the numerator and denominator by the same number doesn't change the value of the fraction; it simply represents the same proportion using different parts.
-
Convert 3/4: To get a denominator of 12, we multiply both the numerator and denominator of 3/4 by 3: (3 x 3) / (4 x 3) = 9/12.
Now that both fractions have the same denominator, we can easily compare them. Since 10/12 > 9/12, we conclude that 5/6 > 3/4.
Method 2: Converting to Decimals
Another effective method is to convert both fractions into decimals. This involves dividing the numerator by the denominator.
-
Convert 5/6 to a decimal: 5 ÷ 6 ≈ 0.8333...
-
Convert 3/4 to a decimal: 3 ÷ 4 = 0.75
By comparing the decimal equivalents, we see that 0.8333... > 0.75, confirming that 5/6 > 3/4. This method is particularly useful when dealing with fractions that are difficult to convert to a common denominator.
Method 3: Visual Representation
For a more intuitive understanding, especially for visual learners, consider representing the fractions visually. Imagine two identical pizzas. One pizza is cut into 6 equal slices, and you have 5 of them (5/6). The other pizza is cut into 4 equal slices, and you have 3 of them (3/4). By visually comparing the amount of pizza you have in each case, it becomes clear that 5/6 represents a larger portion than 3/4.
Method 4: Cross-Multiplication
This method is a shortcut for comparing two fractions without finding a common denominator. Cross-multiply the numerators and denominators:
-
Multiply the numerator of the first fraction (5) by the denominator of the second fraction (4): 5 x 4 = 20
-
Multiply the numerator of the second fraction (3) by the denominator of the first fraction (6): 3 x 6 = 18
Since 20 > 18, it confirms that 5/6 > 3/4.
Why Understanding Fraction Comparison is Important
The ability to compare fractions is fundamental to numerous areas of mathematics and its applications in real life. Here are some examples:
-
Measurement and Conversions: Comparing fractions is essential when dealing with measurements in various units (e.g., inches, centimeters, liters).
-
Data Analysis: Understanding fractions and their comparisons is crucial for interpreting data presented in charts and graphs.
-
Cooking and Baking: Following recipes often involves working with fractions, and comparing them is vital for accurate measurements.
-
Financial Literacy: Understanding percentages (which are essentially fractions out of 100) is crucial for managing finances, understanding interest rates, and interpreting financial data.
-
Probability and Statistics: Fractions play a significant role in probability calculations, where comparing probabilities is essential for decision-making.
Addressing Common Misconceptions
-
Larger Numerator Doesn't Always Mean Larger Fraction: Many students mistakenly assume that a larger numerator automatically means a larger fraction. This is only true if the denominators are the same. For example, 7/10 is smaller than 2/3, even though 7 > 2.
-
Focusing on the Difference Between Numerator and Denominator: Comparing the difference between the numerator and denominator is not a reliable method for comparing fractions.
-
Incorrect Application of Cross-Multiplication: Remember, cross-multiplication only tells you which fraction is larger; it doesn't directly give you the difference between them.
Frequently Asked Questions (FAQ)
-
Q: Are there other methods to compare fractions besides these four?
-
A: Yes, you can also use a number line to visually compare fractions or convert fractions to percentages before comparing them.
-
Q: What if I have more than two fractions to compare?
-
A: You can use any of the above methods, but it's usually most efficient to convert all fractions to a common denominator before comparing them.
-
Q: What if the fractions are negative?
-
A: The principles remain the same, but remember that a smaller negative number is actually greater than a larger negative number. For example, -1/2 > -3/4.
Conclusion
Determining whether 5/6 is greater than 3/4 involves understanding the fundamental concepts of fractions and utilizing effective comparison methods. We have explored four primary approaches: finding a common denominator, converting to decimals, visual representation, and cross-multiplication. Mastering these methods empowers you to confidently compare fractions in any context, solidifying your understanding of this essential mathematical concept. The ability to compare fractions is not just a skill for solving math problems; it's a foundational tool applicable across various disciplines and everyday situations. Remember to choose the method most comfortable and efficient for you, and always double-check your work to ensure accuracy. The more you practice, the more intuitive fraction comparison will become.
Latest Posts
Latest Posts
-
How To Find Dimensions Of Triangle
Aug 27, 2025
-
Write A Conjecture That Relates The Result Of The Process
Aug 27, 2025
-
Lead Ii Nitrate And Potassium Chromate
Aug 27, 2025
-
How To Find The Thickness Of Aluminum Foil
Aug 27, 2025
-
Fraction Divided By Fraction Word Problems
Aug 27, 2025
Related Post
Thank you for visiting our website which covers about Is 5 6 Greater Than 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.