Is 25 Squared A Rational Number
faraar
Aug 27, 2025 · 6 min read
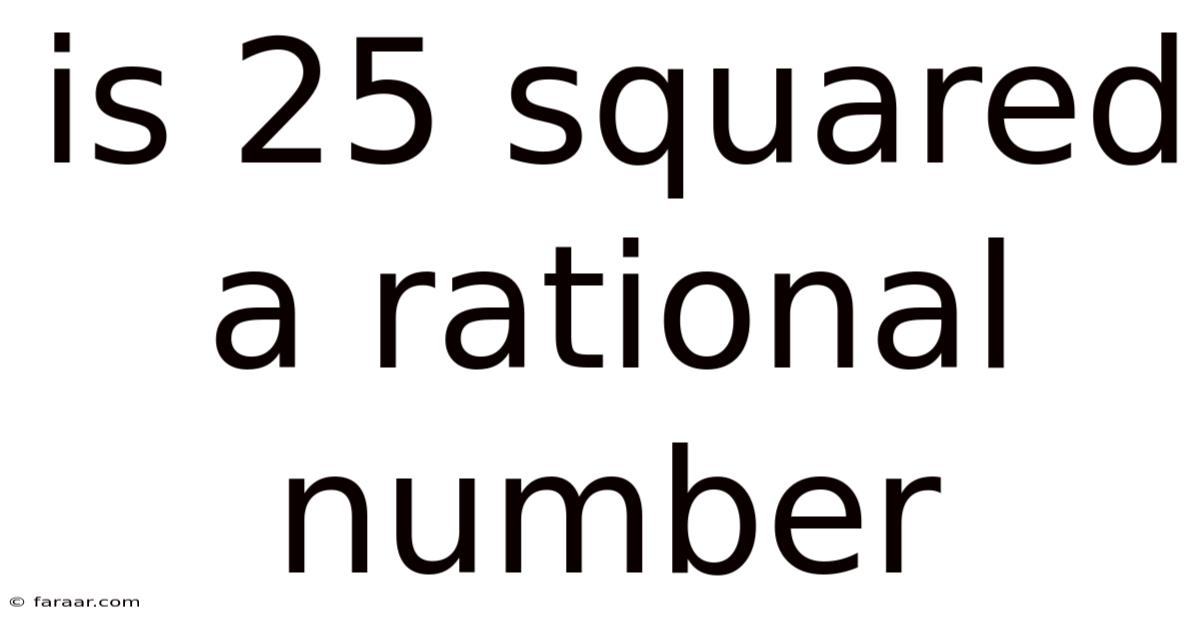
Table of Contents
Is 25 Squared a Rational Number? A Deep Dive into Rationality and Square Roots
This article explores the question: "Is 25 squared a rational number?" While the answer might seem immediately obvious to some, delving into the definition of rational numbers and exploring related concepts provides a valuable opportunity to solidify our understanding of fundamental mathematical principles. We will not only answer the question definitively but also explore the broader context of rational and irrational numbers, including their properties and how they relate to square roots. This exploration will be particularly useful for students learning about number systems and their properties.
Understanding Rational Numbers
Before we tackle the core question, let's clearly define what a rational number is. A rational number is any number that can be expressed as a fraction p/q, where p and q are integers, and q is not equal to zero. Integers include whole numbers (0, 1, 2, 3…) and their negative counterparts (-1, -2, -3…). Crucially, the fraction p/q must be able to represent the number exactly. This means that the decimal representation of a rational number either terminates (ends) or repeats in a predictable pattern.
Examples of rational numbers include:
- 1/2 (0.5) - Terminating decimal
- 2/3 (0.666...) - Repeating decimal
- 4 (4/1) - Integer, also expressible as a fraction
- -3/7 (-0.42857142857...) - Repeating decimal
- 0 (0/1)
Understanding Irrational Numbers
Conversely, an irrational number cannot be expressed as a fraction p/q, where p and q are integers, and q ≠ 0. Their decimal representation neither terminates nor repeats in a predictable pattern. These numbers often arise from operations like taking the square root of non-perfect squares.
Famous examples of irrational numbers include:
- π (pi) ≈ 3.14159...
- e (Euler's number) ≈ 2.71828...
- √2 ≈ 1.41421...
Calculating 25 Squared
Now, let's address the central question: Is 25 squared a rational number? 25 squared (25²) means 25 multiplied by itself: 25 x 25 = 625.
625 is an integer. And as we established earlier, all integers are rational numbers because they can be expressed as a fraction with a denominator of 1 (e.g., 625/1). Therefore, yes, 25 squared is a rational number.
Exploring Square Roots and Rationality
The concept of square roots is closely tied to the rationality of numbers. The square root of a number 'x' (denoted as √x) is a value that, when multiplied by itself, equals x. For example, √25 = 5 because 5 x 5 = 25.
The rationality of a square root depends entirely on the number under the square root sign. If the number is a perfect square (a number that is the square of an integer), then its square root will be an integer and therefore a rational number. However, if the number is not a perfect square, its square root is typically an irrational number.
Here's a breakdown:
-
Perfect Squares and Rationality: √1 = 1 (rational), √4 = 2 (rational), √9 = 3 (rational), √16 = 4 (rational), √25 = 5 (rational), and so on. These all result in integer values, which are rational.
-
Non-Perfect Squares and Irrationality: √2, √3, √5, √6, √7, √8, etc., are all irrational numbers. Their decimal representations are non-terminating and non-repeating.
Proof of Irrationality (for √2 - an example)
Let's illustrate why the square root of a non-perfect square is irrational using a proof by contradiction for the classic example of √2:
-
Assumption: Assume √2 is rational. This means it can be expressed as a fraction p/q, where p and q are integers, q ≠ 0, and the fraction is in its simplest form (meaning p and q have no common factors other than 1).
-
Squaring Both Sides: If √2 = p/q, then squaring both sides gives 2 = p²/q².
-
Rearrangement: This implies 2q² = p². This shows that p² is an even number (because it's equal to 2 times another integer). If p² is even, then p must also be even (because the square of an odd number is always odd).
-
Substituting: Since p is even, we can write it as p = 2k, where k is another integer. Substituting this into the equation 2q² = p², we get 2q² = (2k)² = 4k².
-
Simplifying: Dividing both sides by 2 gives q² = 2k². This shows that q² is also an even number, and therefore q must be even.
-
Contradiction: We've now shown that both p and q are even numbers. This contradicts our initial assumption that p/q is in its simplest form (they share no common factors). This contradiction means our initial assumption that √2 is rational must be false.
-
Conclusion: Therefore, √2 is irrational.
Further Exploration: Decimal Representations and Rationality
The decimal representation of a number offers a practical way to assess its rationality. As mentioned earlier:
-
Terminating Decimals: Decimals that end after a finite number of digits are always rational. For example, 0.75 (3/4), 0.2 (1/5), 0.125 (1/8).
-
Repeating Decimals: Decimals with a repeating pattern of digits are also always rational. For example, 0.333... (1/3), 0.142857142857... (1/7), 0.666... (2/3).
-
Non-Terminating, Non-Repeating Decimals: Decimals that neither terminate nor repeat are irrational. This is the defining characteristic of irrational numbers.
Frequently Asked Questions (FAQs)
Q1: Are all integers rational numbers?
A1: Yes, all integers are rational numbers because they can be expressed as a fraction with a denominator of 1.
Q2: Can a rational number be expressed as a decimal that never ends?
A2: Yes, but if it goes on forever it must repeat a specific pattern of digits. This is different from a non-repeating, infinite decimal which is irrational.
Q3: Are all square roots irrational?
A3: No, only the square roots of non-perfect squares are irrational. The square roots of perfect squares are integers (and therefore rational).
Q4: How can I determine if a number is rational or irrational just by looking at it?
A4: If the number is an integer, it's rational. If it's a simple fraction of integers, it's rational. If it's a non-terminating, non-repeating decimal, it's irrational. For square roots, check if the number under the square root symbol is a perfect square.
Q5: What is the significance of distinguishing between rational and irrational numbers?
A5: The distinction between rational and irrational numbers is fundamental in mathematics. It affects various mathematical operations and plays a crucial role in fields like calculus, geometry, and number theory. Understanding this distinction provides a strong foundation for more advanced mathematical concepts.
Conclusion
In conclusion, the answer to the question "Is 25 squared a rational number?" is a resounding yes. 25 squared (625) is an integer, and all integers are rational numbers. This exploration has gone beyond simply answering the question, however, providing a comprehensive overview of rational and irrational numbers, their properties, and the relationship between square roots and rationality. Understanding these concepts forms a crucial cornerstone of mathematical literacy and provides a solid basis for tackling more complex mathematical problems in the future. The distinction between rational and irrational numbers is not just a theoretical exercise; it’s a fundamental concept that underpins a vast amount of mathematical theory and application.
Latest Posts
Latest Posts
-
Is Acoustic Guitar Easier Than Electric
Aug 27, 2025
-
What Percentage Of 30 Is 20
Aug 27, 2025
-
Does The Comma Go In The Quotation Marks
Aug 27, 2025
-
Convert 34 Degrees Celsius To Fahrenheit
Aug 27, 2025
-
Does A Comma Come Before Or After Quotation Marks
Aug 27, 2025
Related Post
Thank you for visiting our website which covers about Is 25 Squared A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.