Is 2 3 Equal To 1 2
faraar
Sep 09, 2025 · 5 min read
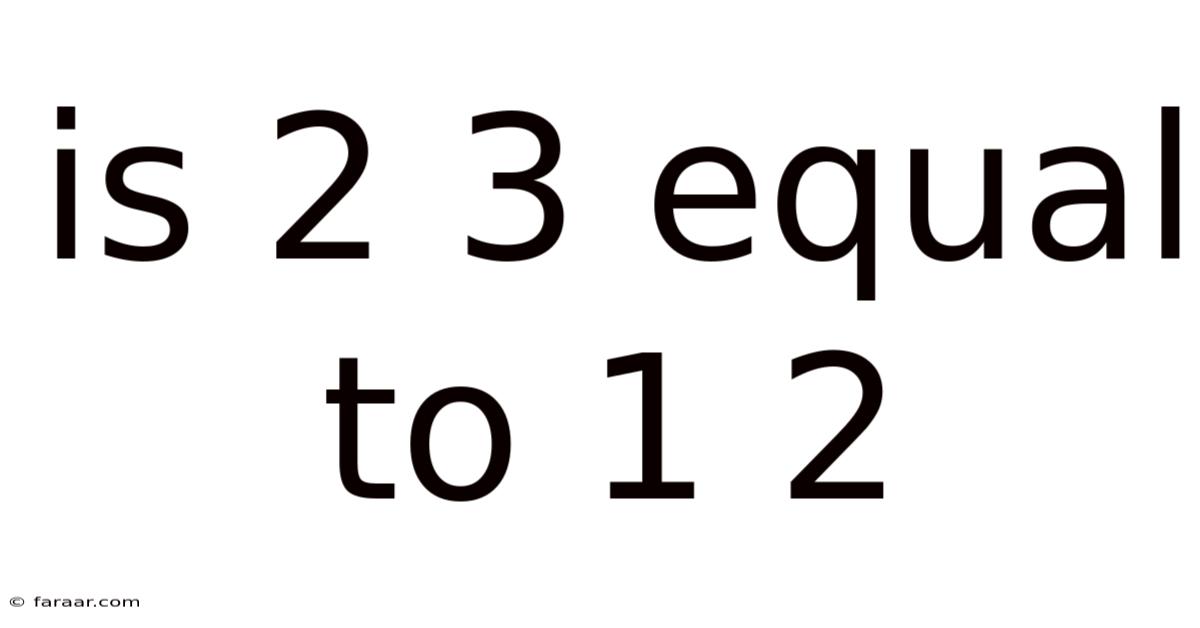
Table of Contents
Is 2/3 Equal to 1/2? Understanding Fractions and Equivalence
The question, "Is 2/3 equal to 1/2?", is a fundamental one in understanding fractions. At first glance, the answer might seem obvious: no. However, a deeper exploration reveals crucial concepts about fraction equivalence, representation, and practical application. This article will not only answer the question definitively but also delve into the underlying mathematical principles, providing a comprehensive understanding of fractions and their manipulations.
Introduction to Fractions
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, in the fraction 2/3, the whole is divided into three equal parts, and we are considering two of those parts.
Understanding the Difference Between 2/3 and 1/2
Visually, the difference becomes clear. Imagine a pizza. If you divide the pizza into three equal slices and take two, you have 2/3 of the pizza. If you divide the same pizza into two equal halves and take one, you have 1/2 of the pizza. Clearly, two slices out of three is a larger portion than one slice out of two.
Numerically, the values are distinct. 2/3 is approximately 0.667, while 1/2 is exactly 0.5. This numerical difference underscores the fact that 2/3 and 1/2 represent different quantities. Therefore, the answer to the initial question is a resounding no, 2/3 is not equal to 1/2.
Equivalent Fractions: The Concept of Simplification and Expansion
While 2/3 and 1/2 are not equal, the concept of equivalent fractions is crucial. Equivalent fractions represent the same proportion or quantity even though they look different. They can be obtained by multiplying or dividing both the numerator and the denominator by the same non-zero number.
For example, 1/2 is equivalent to 2/4 (multiply both by 2), 3/6 (multiply both by 3), 4/8 (multiply both by 4), and so on. All these fractions represent the same half.
Similarly, 2/3 is equivalent to 4/6, 6/9, 8/12, and so forth. These fractions all represent two-thirds of a whole.
Comparing Fractions: Methods and Techniques
To compare fractions effectively, several methods can be used. The simplest approach, if the denominators are the same, is to compare the numerators directly. The fraction with the larger numerator is the larger fraction. However, when the denominators differ, we need to find a common denominator or convert the fractions into decimals.
Method 1: Finding a Common Denominator
This involves finding a common multiple of the denominators. For 2/3 and 1/2, the least common multiple (LCM) of 3 and 2 is 6. We then rewrite each fraction with a denominator of 6:
- 2/3 = (2 x 2) / (3 x 2) = 4/6
- 1/2 = (1 x 3) / (2 x 3) = 3/6
Now, comparing 4/6 and 3/6, it's clear that 4/6 (or 2/3) is greater than 3/6 (or 1/2).
Method 2: Converting to Decimals
Another method is to convert the fractions to decimals by dividing the numerator by the denominator:
- 2/3 ≈ 0.667
- 1/2 = 0.5
Comparing the decimal values confirms that 2/3 is larger than 1/2.
The Importance of Understanding Fraction Equivalence
The concept of equivalent fractions is fundamental in various mathematical operations, including addition, subtraction, multiplication, and division of fractions. It’s essential for simplifying complex fractions, solving equations, and understanding ratios and proportions. Without a solid grasp of equivalent fractions, performing these operations accurately becomes significantly more challenging.
Practical Applications of Fractions
Fractions are ubiquitous in everyday life. We encounter them in:
- Cooking and Baking: Recipes often involve fractional measurements (e.g., 1/2 cup of sugar, 2/3 cup of flour).
- Measurements: Lengths, weights, and volumes are frequently expressed using fractions (e.g., 2 1/2 inches, 1/4 kilogram).
- Money: Dealing with cents involves fractions of a dollar (e.g., $2.50 is $2 and 1/2).
- Probability: Calculating probabilities often involves fractions (e.g., the probability of flipping heads is 1/2).
- Data Representation: Fractions are essential in visualizing and analyzing data, particularly in charts and graphs.
Frequently Asked Questions (FAQ)
Q1: How can I simplify fractions?
To simplify a fraction, find the greatest common divisor (GCD) of the numerator and the denominator. Then, divide both the numerator and the denominator by the GCD. For example, to simplify 6/9, the GCD of 6 and 9 is 3. Dividing both by 3 gives 2/3.
Q2: How do I add or subtract fractions?
To add or subtract fractions, they must have the same denominator. If they don't, find a common denominator first. Then, add or subtract the numerators and keep the denominator the same. For example: 1/2 + 1/3 = (3/6) + (2/6) = 5/6
Q3: How do I multiply fractions?
Multiply the numerators together and multiply the denominators together. For example: (1/2) x (2/3) = (1 x 2) / (2 x 3) = 2/6 = 1/3
Q4: How do I divide fractions?
To divide a fraction by another fraction, invert the second fraction (reciprocal) and then multiply. For example: (1/2) ÷ (1/3) = (1/2) x (3/1) = 3/2
Q5: What is an improper fraction?
An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 5/3, 7/4). These can be converted to mixed numbers (e.g., 1 2/3, 1 3/4).
Conclusion: Mastering Fractions for a Brighter Future
Understanding fractions is crucial for success in mathematics and numerous real-world applications. While the simple question of whether 2/3 equals 1/2 has a straightforward answer (no), exploring the concepts of fraction equivalence, comparison, and manipulation provides a deeper appreciation of this fundamental mathematical concept. Mastering these skills will equip you with essential problem-solving tools and enhance your ability to navigate various quantitative challenges in your academic and professional life. Remember, practice is key! The more you work with fractions, the more comfortable and proficient you will become. Don't hesitate to seek help from teachers, tutors, or online resources if you encounter difficulties. With consistent effort and a willingness to learn, you can confidently conquer the world of fractions.
Latest Posts
Latest Posts
-
Even And Odd Properties Of Trigonometric Functions
Sep 09, 2025
-
How Many Times Greater Is The Value
Sep 09, 2025
-
What Happens When You Add A Negative To A Positive
Sep 09, 2025
-
12 Rounded To The Nearest Tenth
Sep 09, 2025
-
Which Category Do Both Shapes Belong To
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Is 2 3 Equal To 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.