Is 1 3 Plus 1 3 2 3
faraar
Sep 16, 2025 · 6 min read
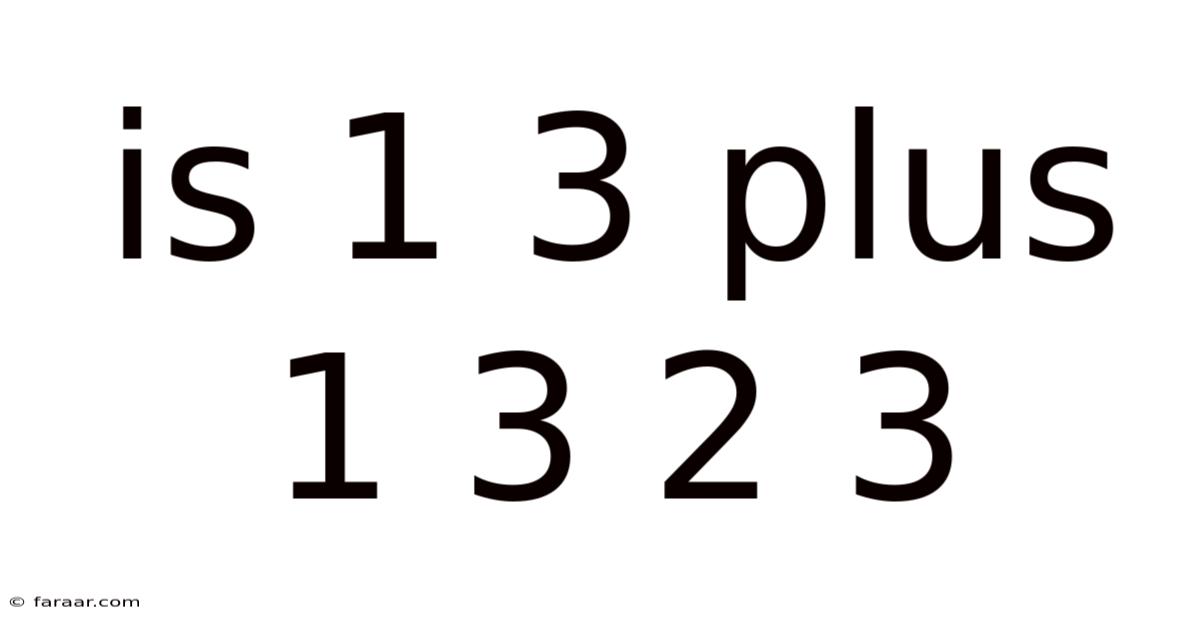
Table of Contents
Is 1/3 Plus 1/3 = 2/3? A Deep Dive into Fraction Addition
This article explores the seemingly simple equation, 1/3 + 1/3 = 2/3, delving into the underlying principles of fraction addition, common misconceptions, and practical applications. We'll unravel the fundamental concepts, providing a clear and comprehensive understanding suitable for learners of all levels. Understanding fraction addition is a crucial building block in mathematics, impacting various fields from baking to engineering. Let's explore why 1/3 + 1/3 truly equals 2/3 and how this knowledge empowers us in everyday life.
Understanding Fractions: A Refresher
Before diving into the addition, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a numerator (the top number) over a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/3, the numerator is 1, and the denominator is 3. This signifies one part out of three equal parts.
Adding Fractions with Common Denominators
The key to adding fractions is to have a common denominator. This means the bottom numbers (denominators) of the fractions being added must be the same. Fortunately, in our example, 1/3 + 1/3, both fractions already share the common denominator of 3. When denominators are the same, adding fractions is straightforward:
- Add the numerators: Add the top numbers (1 + 1 = 2).
- Keep the denominator the same: The denominator remains unchanged (it stays as 3).
Therefore, 1/3 + 1/3 = 2/3.
Visualizing the Addition
Visual representations can make abstract concepts like fractions much easier to grasp. Imagine a pie cut into three equal slices. 1/3 represents one slice. Adding another 1/3 means taking another slice. Together, you have two slices out of three, which is visually represented as 2/3. This simple visualization solidifies the understanding of the equation's result.
Adding Fractions with Unlike Denominators
While our example used fractions with a common denominator, let's expand our understanding to include situations where the denominators differ. For instance, consider adding 1/2 and 1/4. These fractions have unlike denominators. To add them, we must find a least common denominator (LCD).
The LCD is the smallest number that both denominators can divide into evenly. In this case, the LCD of 2 and 4 is 4. We convert each fraction to an equivalent fraction with the LCD as the denominator:
- 1/2 is equivalent to 2/4 (multiply both numerator and denominator by 2)
Now we can add:
2/4 + 1/4 = 3/4
The Importance of Common Denominators
The concept of a common denominator is paramount. Without it, we're essentially adding unlike units. You can't directly add apples and oranges; you need a common unit of measurement (like fruit) to combine them meaningfully. Similarly, fractions must have a common denominator before we can add their numerators.
Real-World Applications of Fraction Addition
Fraction addition isn't just a classroom exercise; it's a practical skill used in various everyday scenarios:
- Cooking and Baking: Recipes often involve fractions. Adding ingredients, such as 1/2 cup of flour and 1/4 cup of sugar, requires accurate fraction addition.
- Construction and Engineering: Precise measurements are essential in these fields, frequently using fractions of inches or meters.
- Finance: Calculating portions of budgets, understanding interest rates, or dividing shares often involve fractions and their addition.
- Data Analysis: Representing data using fractions and performing calculations often involves adding fractions to arrive at meaningful results.
Common Misconceptions about Fraction Addition
Even seemingly simple operations like adding fractions can lead to misunderstandings. Some common misconceptions include:
- Adding numerators and denominators directly: A common mistake is adding the numerators and denominators separately (e.g., believing 1/3 + 1/3 = 2/6). This is incorrect. Remember, only the numerators are added; the denominator remains unchanged when the denominators are common.
- Forgetting to find a common denominator: When adding fractions with unlike denominators, failing to find the least common denominator leads to an incorrect result. Always ensure you have a common denominator before adding.
- Incorrect simplification: After adding fractions, it's crucial to simplify the result to its lowest terms. For example, 2/4 should be simplified to 1/2.
Advanced Fraction Operations
Beyond simple addition, understanding fractions extends to more complex operations like subtraction, multiplication, and division.
- Subtraction: Similar to addition, fractions must have a common denominator before subtraction can be performed. The numerators are then subtracted, and the denominator remains the same.
- Multiplication: To multiply fractions, multiply the numerators together and multiply the denominators together. Simplification is often required after multiplication.
- Division: To divide fractions, invert the second fraction (reciprocal) and then multiply.
Addressing Potential Queries (FAQ)
Q: What if the fractions have different denominators?
A: Find the least common denominator (LCD) for the fractions and convert each fraction into an equivalent fraction with that denominator before adding.
Q: How do I simplify a fraction?
A: Find the greatest common divisor (GCD) of the numerator and denominator. Divide both the numerator and denominator by the GCD to simplify the fraction to its lowest terms. For example, to simplify 6/9, the GCD is 3. Dividing both by 3 gives 2/3.
Q: Is there a way to check if my answer is correct?
A: Estimating the answer before calculation can help. For example, you know that 1/3 is slightly less than 1/2. Therefore, 1/3 + 1/3 should be slightly less than 1. This estimation helps to identify gross errors. Using visual representations, like dividing a pie or circle, can also serve as a check.
Q: Why is understanding fractions important?
A: Fractions are fundamental to many areas of mathematics and crucial for solving real-world problems involving parts of wholes, proportions, ratios, and more. They form the foundation for more advanced mathematical concepts.
Conclusion: The Power of Understanding Fractions
The seemingly simple equation 1/3 + 1/3 = 2/3 underscores the importance of a firm grasp of fraction fundamentals. While the addition itself is straightforward when the denominators are common, understanding the underlying principles, addressing common misconceptions, and appreciating the broad applications of fractions are key to mathematical proficiency. Mastering fraction addition provides a solid base for tackling more complex mathematical concepts and solving real-world problems across numerous fields. By appreciating the visual and practical aspects of fractions, we can move beyond rote memorization and develop a true, intuitive understanding of these fundamental mathematical building blocks. Remember, a strong foundation in fractions paves the way for future success in mathematics and beyond.
Latest Posts
Latest Posts
-
How To Dilate On A Coordinate Plane
Sep 16, 2025
-
Write The Sentence As An Equation
Sep 16, 2025
-
What Changes In Color When Bromine Reacts With An Alkene
Sep 16, 2025
-
What Is 1 3 Divided By 4 In Fraction Form
Sep 16, 2025
-
Isopropyl Alcohol Density In G Ml
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Is 1 3 Plus 1 3 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.