How To Factor 2x 2 5x 3
faraar
Sep 19, 2025 · 6 min read
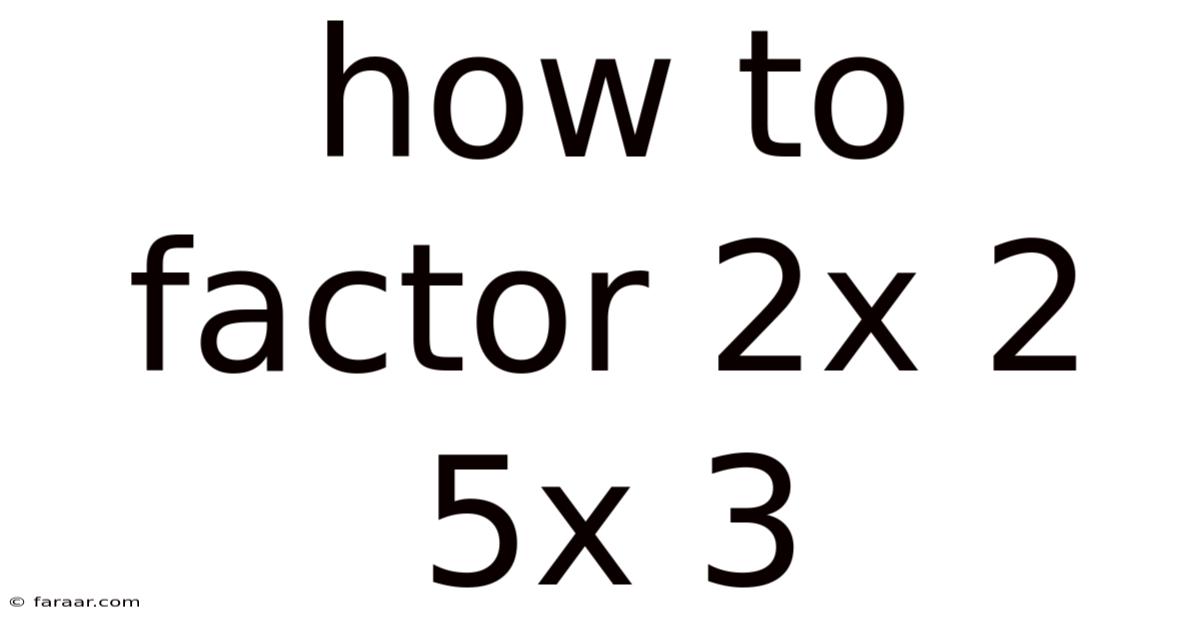
Table of Contents
How to Factor 2x² + 5x + 3: A Comprehensive Guide
Factoring quadratic expressions like 2x² + 5x + 3 is a fundamental skill in algebra. Understanding how to factor these expressions opens doors to solving quadratic equations, simplifying complex algebraic expressions, and grasping more advanced mathematical concepts. This comprehensive guide will walk you through the process step-by-step, explaining the underlying principles and providing various methods to tackle such problems. We'll explore both the trial-and-error method and the AC method, ensuring you develop a strong understanding of factoring quadratic trinomials.
Understanding Quadratic Expressions
Before diving into the factoring process, let's clarify what a quadratic expression is. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually 'x') is 2. It generally takes the form ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. In our example, 2x² + 5x + 3, a = 2, b = 5, and c = 3.
Method 1: Trial and Error (Factoring by Inspection)
This method relies on your intuition and understanding of how binomial multiplication works. We're looking for two binomials that, when multiplied together, result in 2x² + 5x + 3. Let's break it down:
-
Consider the first term (2x²): The only way to obtain 2x² through multiplication is by multiplying 2x and x. Therefore, our binomials will start like this: (2x )(x ).
-
Consider the last term (3): The factors of 3 are 1 and 3. We need to place these numbers in the binomials in a way that, when multiplied using the FOIL method (First, Outer, Inner, Last), will give us the middle term (5x).
-
Testing the possibilities: Let's try both possible arrangements:
- (2x + 1)(x + 3): Using FOIL, we get 2x² + 6x + x + 3 = 2x² + 7x + 3. This is not correct.
- (2x + 3)(x + 1): Using FOIL, we get 2x² + 2x + 3x + 3 = 2x² + 5x + 3. This is correct!
Therefore, the factored form of 2x² + 5x + 3 is (2x + 3)(x + 1).
Method 2: The AC Method (Factoring by Grouping)
The AC method is a more systematic approach that works well even when the trial-and-error method becomes more challenging. It involves these steps:
-
Find the product AC: In our example, a = 2 and c = 3, so AC = 2 * 3 = 6.
-
Find two numbers that add up to B and multiply to AC: We need two numbers that add up to b (which is 5) and multiply to 6. These numbers are 2 and 3 (2 + 3 = 5 and 2 * 3 = 6).
-
Rewrite the middle term: Replace the middle term (5x) with the two numbers we found, using x as a factor: 2x² + 2x + 3x + 3.
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
- 2x² + 2x = 2x(x + 1)
- 3x + 3 = 3(x + 1)
-
Factor out the common binomial: Notice that both terms now have a common factor of (x + 1). Factor this out: (x + 1)(2x + 3).
Therefore, using the AC method, we again arrive at the factored form: (2x + 3)(x + 1).
Why Factoring is Important
The ability to factor quadratic expressions is crucial for several reasons:
-
Solving Quadratic Equations: Many quadratic equations are easily solved by factoring. Once factored, setting each factor equal to zero allows you to find the roots (solutions) of the equation. For example, if 2x² + 5x + 3 = 0, then (2x + 3)(x + 1) = 0, leading to the solutions x = -3/2 and x = -1.
-
Simplifying Expressions: Factoring simplifies complex algebraic expressions, making them easier to manipulate and understand. This is essential in higher-level mathematics and applications.
-
Graphing Parabolas: The factored form of a quadratic expression reveals the x-intercepts of its corresponding parabola (the graph of the quadratic function). The x-intercepts are the points where the parabola crosses the x-axis.
-
Foundation for Advanced Algebra: Factoring is a building block for more advanced algebraic concepts, such as partial fraction decomposition and solving polynomial equations of higher degrees.
Dealing with More Complex Quadratic Expressions
The methods discussed above can be adapted to factor more complex quadratic expressions. However, some expressions might require more advanced techniques or might not be factorable using integers.
-
Expressions with a negative leading coefficient: If 'a' is negative, it's often helpful to factor out a -1 first to simplify the expression.
-
Expressions with a greatest common factor (GCF): Always look for a GCF among the terms before attempting to factor the quadratic itself. For instance, in the expression 6x² + 15x + 9, the GCF is 3. Factoring out 3 leaves us with 3(2x² + 5x + 3), which we already know how to factor.
-
Unfactorable quadratics: Not all quadratic expressions can be factored using integers. In such cases, the quadratic formula or other numerical methods are required to find the roots.
-
Quadratics with irrational or complex roots: Some quadratic equations have roots that are irrational numbers (like √2) or complex numbers (involving the imaginary unit 'i'). These require more advanced techniques to solve and often cannot be factored using simple integers.
Frequently Asked Questions (FAQ)
-
Q: What if the quadratic expression is not in standard form (ax² + bx + c)?
A: Before factoring, always rearrange the expression into standard form. This makes it easier to identify the coefficients a, b, and c.
-
Q: Can I use a calculator or software to factor quadratic expressions?
A: While calculators and software can help, understanding the underlying principles and methods is crucial for developing a strong mathematical foundation. Use these tools to verify your answers, but prioritize learning the manual methods.
-
Q: What if I get stuck while using the trial-and-error method?
A: The AC method provides a more systematic approach. If you're struggling with trial and error, switch to the AC method. Practice is key; the more you practice, the faster and more intuitive the trial-and-error method will become.
-
Q: Is there only one correct way to factor a quadratic expression?
A: No. While the order of the factors might differ (e.g., (x+1)(2x+3) is equivalent to (2x+3)(x+1)), the factored form will always be equivalent.
Conclusion
Factoring quadratic expressions is a vital skill in algebra. This guide has presented two effective methods – trial and error and the AC method – empowering you to factor a wide range of quadratic trinomials. Remember to practice regularly to build your proficiency. Mastering this skill will lay a solid foundation for tackling more complex algebraic problems and unlocking a deeper understanding of mathematical concepts. Through consistent practice and understanding of the underlying principles, you'll confidently approach any quadratic expression and successfully factor it. Don't be afraid to explore different methods and find the one that best suits your learning style. The journey to mastering algebra is a rewarding one, and factoring is a crucial step along the way!
Latest Posts
Latest Posts
-
Draw A Square That Is Not A Rhombus
Sep 19, 2025
-
How To Graph 3x Y 1
Sep 19, 2025
-
How To Factor X 2 X
Sep 19, 2025
-
The Sarbanes Oxley Act Of 2002 Is A Governmental Response To
Sep 19, 2025
-
Graph The Set On The Number Line
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about How To Factor 2x 2 5x 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.