How Much Is Half Of 2/3
faraar
Sep 17, 2025 · 5 min read
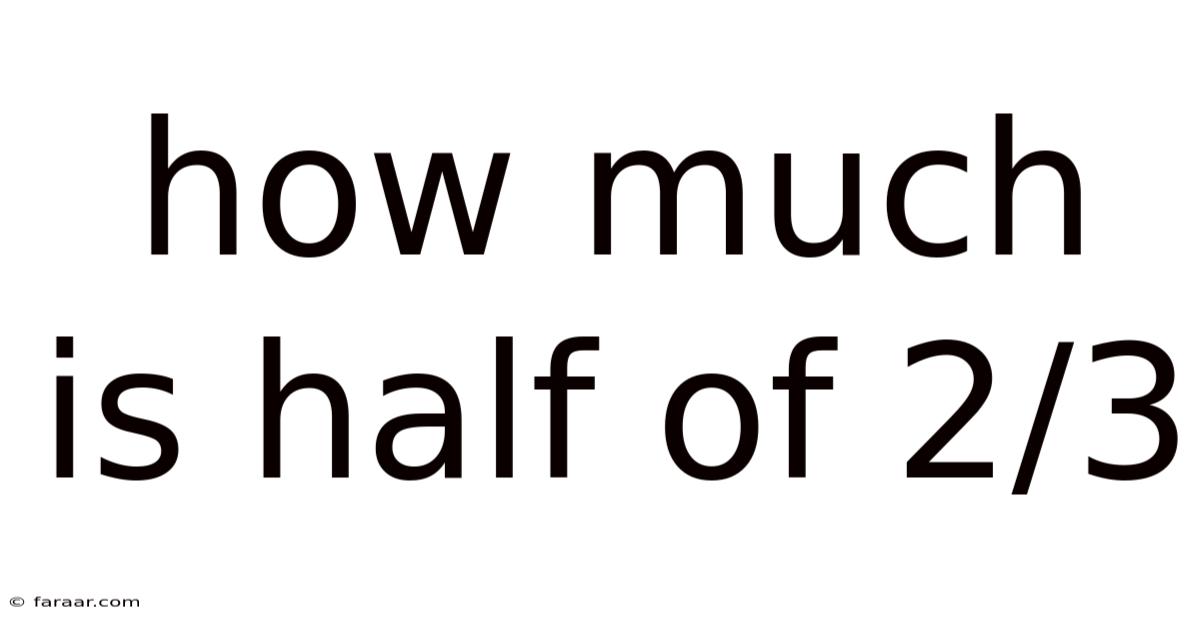
Table of Contents
How Much is Half of 2/3? A Deep Dive into Fractions
Finding half of 2/3 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding this seemingly basic calculation opens the door to a broader understanding of fractions, their manipulation, and their importance in various aspects of mathematics and everyday life. This article will not only provide the answer but also delve into the underlying principles, explore different methods of solving the problem, and extend the concept to more complex scenarios. We'll also address common misconceptions and frequently asked questions.
Introduction: Understanding Fractions
Before we tackle the problem of finding half of 2/3, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 2/3, the numerator is 2, and the denominator is 3. This means we have 2 out of 3 equal parts of a whole.
Finding Half of 2/3: The Calculation
The problem asks us to find half of 2/3. This can be expressed mathematically as (1/2) * (2/3). There are several ways to solve this:
Method 1: Multiplication of Fractions
The simplest method involves directly multiplying the numerators and the denominators.
- Multiply the numerators: 1 * 2 = 2
- Multiply the denominators: 2 * 3 = 6
This gives us the fraction 2/6. However, this fraction can be simplified.
Method 2: Simplification of Fractions
To simplify a fraction, we find the greatest common divisor (GCD) of the numerator and the denominator and divide both by it. The GCD of 2 and 6 is 2.
- Divide the numerator by the GCD: 2 / 2 = 1
- Divide the denominator by the GCD: 6 / 2 = 3
Therefore, the simplified fraction is 1/3. So, half of 2/3 is 1/3.
Method 3: Visual Representation
Imagine a circle divided into three equal parts. Shading two of these parts represents the fraction 2/3. Now, divide each of the three parts in half. You will now have six equal parts. Half of the original shaded area (2/3) will encompass one out of these six parts, which is represented by the fraction 1/3. This visual approach helps to solidify the understanding of the mathematical calculation.
Extending the Concept: Working with More Complex Fractions
The principles applied to finding half of 2/3 can be extended to more complex scenarios involving different fractions and operations. For instance, let's consider finding 3/4 of 2/3.
(3/4) * (2/3) = (32) / (43) = 6/12
This fraction can be simplified to 1/2 by dividing both the numerator and the denominator by their GCD, which is 6. This demonstrates the consistent application of fraction multiplication and simplification.
Real-World Applications of Fractions
Fractions are not merely abstract mathematical concepts; they are integral to various aspects of daily life. Consider these examples:
- Cooking: Recipes often call for fractional amounts of ingredients, like 1/2 cup of sugar or 2/3 cup of flour.
- Measurements: Construction, engineering, and other trades heavily rely on precise measurements involving fractions of inches or centimeters.
- Finance: Understanding fractions is crucial for calculating interest rates, discounts, and proportions in financial transactions.
- Data Analysis: Fractions are fundamental in representing and interpreting data, such as percentages and proportions.
Common Misconceptions and Pitfalls
A common misconception when working with fractions is the incorrect application of operations. Remember that multiplying fractions involves multiplying the numerators and denominators separately, while adding or subtracting fractions requires a common denominator. Failing to simplify fractions after calculations can lead to inaccurate results and make further computations more complicated.
Frequently Asked Questions (FAQ)
-
Q: Can I divide 2/3 by 2 to find half of it?
- A: Yes, dividing by 2 is equivalent to multiplying by 1/2. Both methods will yield the same result: 1/3.
-
Q: What if I have a mixed number instead of a simple fraction?
- A: Convert the mixed number into an improper fraction before performing any operations. For example, to find half of 1 1/2, first convert 1 1/2 to 3/2, then multiply by 1/2: (1/2) * (3/2) = 3/4.
-
Q: How can I improve my understanding of fractions?
- A: Practice is key. Work through various problems involving different fractions and operations. Utilize visual aids like diagrams and charts to solidify your understanding.
Conclusion: Mastering Fractions - A Foundation for Mathematical Success
Finding half of 2/3, while seemingly straightforward, serves as a gateway to a deeper understanding of fractional arithmetic. Mastering the principles of fraction manipulation is not only essential for solving mathematical problems but also for navigating various real-world situations that involve proportions, measurements, and data interpretation. Through consistent practice and a clear grasp of the underlying concepts, one can build a strong foundation in mathematics and confidently tackle more complex challenges involving fractions. Remember to always simplify your answers to their lowest terms for clarity and accuracy. By understanding these fundamental concepts, you'll be well-equipped to approach more complex mathematical problems with confidence and ease. The seemingly simple act of finding half of 2/3 opens the door to a world of mathematical possibilities.
Latest Posts
Latest Posts
-
What Is The Value Of 0 In 302
Sep 17, 2025
-
How Many Inches Are In 3 5 Yards
Sep 17, 2025
-
What Is The Measurement Of Angle L
Sep 17, 2025
-
Mass Of 4 Moles Of Helium
Sep 17, 2025
-
Find The Average Velocity Over The Interval
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about How Much Is Half Of 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.