How Many 2 5 Are In 4
faraar
Sep 23, 2025 · 5 min read
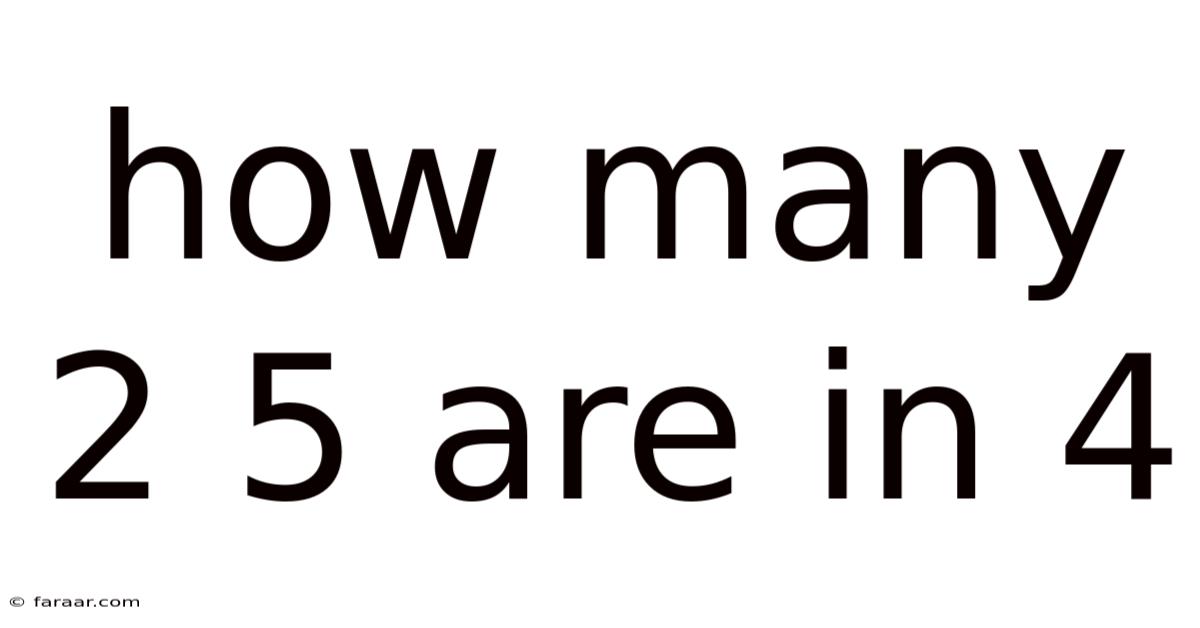
Table of Contents
How Many 2.5s Are in 4? A Deep Dive into Division and Fractions
This seemingly simple question – "How many 2.5s are in 4?" – opens the door to a deeper understanding of division, fractions, and decimals. While the answer might seem immediately obvious to some, exploring the different ways to solve this problem reveals fundamental mathematical concepts crucial for more advanced studies. This article will guide you through various methods, explain the underlying principles, and even touch upon real-world applications.
Understanding the Question: Division as Repeated Subtraction
At its core, the question "How many 2.5s are in 4?" is asking how many times you can subtract 2.5 from 4 before reaching zero (or a number less than 2.5). This is the essence of division. Division is simply repeated subtraction.
Let's visualize this:
Imagine you have 4 pizzas. Each person eats 2.5 pizzas. How many people can you feed? This is the same question as how many 2.5s are in 4.
Method 1: Long Division
The most straightforward method is long division. This method is a systematic way to perform division, especially when dealing with decimals.
-
Set up the division: Write the problem as 4 ÷ 2.5.
-
Adjust for decimals: To make the division easier, we can multiply both the dividend (4) and the divisor (2.5) by 10 to remove the decimal point. This gives us 40 ÷ 25.
-
Perform long division:
1.6 25 | 40.0 -25 --- 150 -150 --- 0 -
The answer: The result is 1.6. Therefore, there are 1.6 instances of 2.5 in 4.
Method 2: Converting to Fractions
Another approach involves converting the numbers into fractions. This method offers a deeper understanding of the relationship between decimals and fractions.
-
Express 2.5 as a fraction: 2.5 can be written as 2 ½ or 5/2.
-
Rewrite the problem: The question becomes "How many 5/2 are in 4?" This is equivalent to 4 ÷ (5/2).
-
Invert and multiply: When dividing by a fraction, we invert the second fraction (the divisor) and multiply. This becomes 4 x (2/5).
-
Simplify: 4 x (2/5) = 8/5.
-
Convert back to decimal: 8/5 = 1.6
Again, we arrive at the answer: 1.6.
Method 3: Using Proportions
Proportions provide a different perspective on the problem. We can set up a proportion to solve for the unknown number of 2.5s in 4.
Let 'x' represent the number of 2.5s in 4. We can set up the proportion:
2.5 / 1 = 4 / x
Cross-multiplying, we get:
2.5x = 4
Solving for x:
x = 4 / 2.5 = 1.6
Understanding the Result: The Significance of 1.6
The answer, 1.6, might seem unusual at first. It's not a whole number, indicating that there isn't a whole number of 2.5s contained perfectly within 4. The 1 represents one complete instance of 2.5, while the .6 represents 6/10 or 3/5 of another 2.5. This highlights that division doesn't always yield whole numbers.
Real-World Applications
Understanding how to solve problems like "How many 2.5s are in 4?" is essential in many real-world scenarios:
-
Resource Allocation: Imagine you have 4 liters of paint and each coat requires 2.5 liters. You can apply only 1.6 coats.
-
Financial Calculations: If you have $4 and each item costs $2.50, you can afford 1.6 items.
-
Measurement Conversions: Many unit conversions involve dividing or finding proportions, similar to this problem.
Expanding the Concept: Variations and Extensions
The core concept explored here – finding how many times one number fits into another – extends to many other mathematical problems:
-
Dividing larger numbers: The same techniques (long division, fractions, proportions) can be applied to divide larger numbers with decimals.
-
Dividing by fractions: Mastering the process of dividing by fractions (inverting and multiplying) is crucial for various mathematical operations.
-
Working with different units: The principles can be applied to problems involving different units of measurement (e.g., converting kilometers to miles).
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Absolutely! A calculator provides a quick and efficient way to solve 4 ÷ 2.5.
Q: What if the numbers were more complex, involving more decimal places?
A: The same methods would apply. Long division might become more involved, but the principles remain the same. Using a calculator would be particularly helpful in these cases.
Q: Is there a specific formula for this type of problem?
A: There's no single formula, but the core concept is division. You can express the problem as a ÷ b, where 'a' is the number you're dividing (4 in this case) and 'b' is the number you're dividing by (2.5 in this case).
Q: Why is understanding this concept important?
A: This fundamental concept underpins many areas of mathematics and its real-world applications. A strong grasp of division is critical for various fields, including science, engineering, and finance.
Conclusion
The seemingly simple question "How many 2.5s are in 4?" provides a rich opportunity to explore core mathematical concepts. Through long division, fraction conversion, and proportions, we arrive at the answer 1.6, demonstrating the importance of understanding that division doesn't always result in whole numbers. Mastering this concept strengthens your foundation in mathematics and prepares you to tackle more complex problems in various fields. The methods explored here are applicable to a wide range of division problems, emphasizing the importance of understanding the underlying principles rather than just memorizing procedures. Remember to practice and explore different methods to build a solid understanding of division and its applications.
Latest Posts
Latest Posts
-
Which Sequence Has A Common Ratio Of 3
Sep 23, 2025
-
1 Kilo Of Rice Is How Many Cups
Sep 23, 2025
-
Choose The Three Parts Of A Nucleotide
Sep 23, 2025
-
How To Find Equation Of A Vertical Line
Sep 23, 2025
-
Common Denominator For 3 4 5
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about How Many 2 5 Are In 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.