How Many 1/6 Are In 2/3
faraar
Sep 12, 2025 · 5 min read
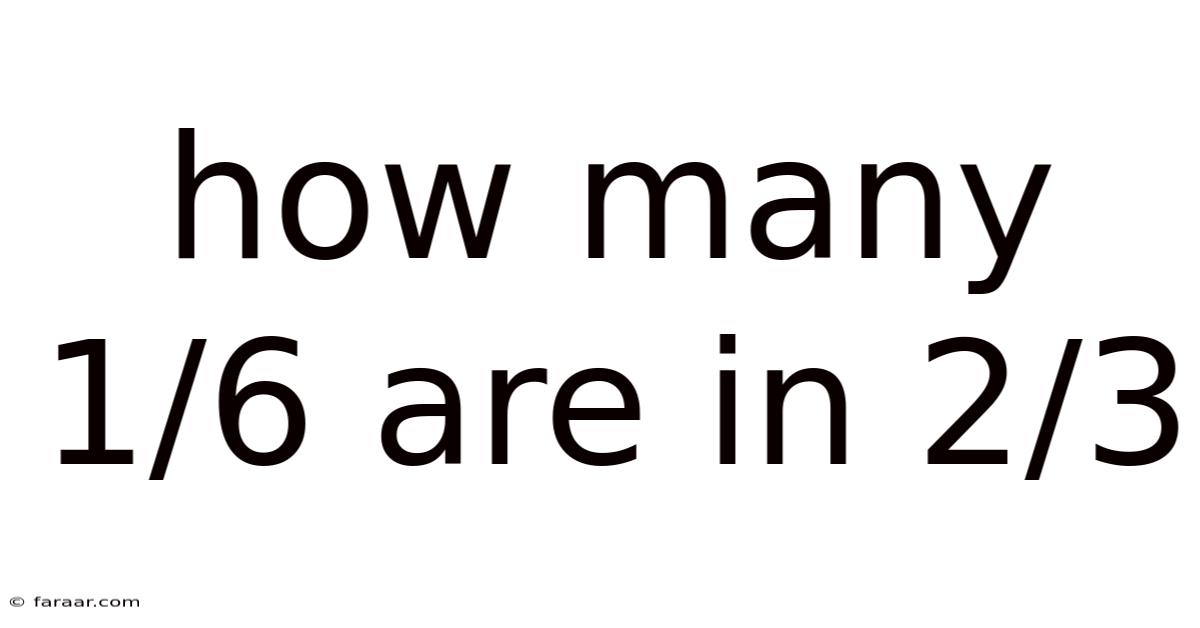
Table of Contents
How Many 1/6s Are in 2/3? A Deep Dive into Fractions
Understanding fractions is fundamental to mathematics, and mastering them unlocks a world of possibilities in various fields. This article will guide you through the process of determining how many 1/6s are in 2/3, not just providing the answer, but also explaining the underlying concepts and offering different approaches to solve similar problems. We'll explore various methods, from simple visualization to the more formal mathematical techniques, ensuring a thorough understanding for learners of all levels.
Introduction: Understanding the Question
The question, "How many 1/6s are in 2/3?" essentially asks us to find how many times the fraction 1/6 goes into the fraction 2/3. This involves a crucial understanding of fraction division. We’re not simply comparing two fractions but rather looking at one fraction as a divisor and the other as a dividend. This is a common problem encountered in various mathematical contexts, from simple arithmetic to more complex algebraic equations.
Method 1: Visual Representation Using Fraction Bars
A visual approach is often the most intuitive way to grasp the concept. Imagine two fraction bars representing the fractions 1/6 and 2/3.
-
Fraction Bar for 1/6: This bar is divided into six equal parts, with one part shaded to represent 1/6.
-
Fraction Bar for 2/3: This bar is divided into three equal parts, with two parts shaded to represent 2/3.
To compare, we need a common denominator. Observe that if we divide the 2/3 bar into six equal parts (by dividing each of the three existing parts in half), we would have 4 shaded parts out of 6. This means 2/3 is equivalent to 4/6.
Therefore, we can see visually that there are four 1/6s in 2/3. Each of the four shaded sections in the 2/3 bar is equal in size to the one shaded section in the 1/6 bar.
Method 2: Converting to a Common Denominator
This method utilizes the fundamental principle of fraction equivalence. To compare or operate on fractions, they need to have the same denominator.
-
Find a Common Denominator: The denominators are 6 and 3. The least common multiple (LCM) of 6 and 3 is 6.
-
Convert Fractions:
- 1/6 already has a denominator of 6.
- To convert 2/3 to have a denominator of 6, we multiply both the numerator and denominator by 2: (2 * 2) / (3 * 2) = 4/6
-
Compare: Now we have 4/6 and 1/6. It's clear that there are four 1/6s in 4/6.
Therefore, there are four 1/6s in 2/3.
Method 3: Fraction Division
This is the most formal mathematical approach. Dividing fractions involves multiplying the first fraction by the reciprocal of the second fraction.
-
Rewrite the Problem as a Division: The problem can be written as (2/3) ÷ (1/6).
-
Find the Reciprocal: The reciprocal of 1/6 is 6/1 (or simply 6).
-
Multiply: Multiply 2/3 by the reciprocal of 1/6: (2/3) * (6/1) = (2 * 6) / (3 * 1) = 12/3
-
Simplify: Simplify the resulting fraction: 12/3 = 4
Therefore, there are four 1/6s in 2/3.
Method 4: Using Decimal Equivalents
This method involves converting the fractions to their decimal equivalents before comparison.
-
Convert to Decimals:
- 1/6 = 0.1666... (repeating decimal)
- 2/3 = 0.6666... (repeating decimal)
-
Divide: Divide the decimal equivalent of 2/3 by the decimal equivalent of 1/6: 0.6666... ÷ 0.1666... ≈ 4
This method might introduce slight inaccuracies due to rounding with repeating decimals, but it provides a reasonable approximation. The exact answer remains 4.
The Mathematical Explanation: Why This Works
The success of these methods hinges on the fundamental properties of fractions and the concept of division. When we ask "How many 1/6s are in 2/3?", we are essentially asking: "What number, when multiplied by 1/6, equals 2/3?" This is represented mathematically as:
x * (1/6) = 2/3
To solve for x, we employ the principles of algebra:
x = 2/3 ÷ 1/6 = 2/3 * 6/1 = 12/3 = 4
This reinforces that the answer is indeed four.
Expanding the Concept: Solving Similar Problems
The methods explained above can be applied to solve similar problems involving different fractions. For instance:
- How many 1/4s are in 3/2? (Answer: 6)
- How many 2/5s are in 4/10? (Answer: 2)
- How many 3/8s are in 9/16? (Answer: 3/2 or 1.5)
Remember to always:
- Find a common denominator (for visual or comparison methods).
- Use the reciprocal when dividing fractions (for the formal division method).
- Simplify your final answer.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this? A: Yes, most calculators can handle fraction division. However, understanding the underlying concepts is crucial for problem-solving and deeper mathematical comprehension.
-
Q: Why is finding a common denominator important? A: A common denominator allows you to directly compare the sizes of the fractions, making it easier to visualize and calculate how many times one fraction "fits" into the other.
-
Q: What if the fractions don't have a common denominator? A: You will need to find one before you can effectively compare or divide the fractions. You can find the least common multiple (LCM) of the denominators to determine the appropriate common denominator.
-
Q: Are there other ways to solve this problem? A: While the methods mentioned are the most common and straightforward, more advanced techniques using algebraic manipulation might be employed for more complex scenarios.
Conclusion: Mastering Fraction Division
Understanding how many 1/6s are in 2/3, and more broadly, mastering fraction division, is a cornerstone of mathematical literacy. By applying the different methods explained in this article – visualization, common denominator conversion, formal fraction division, and decimal conversion – you gain a comprehensive understanding of the underlying principles. Remember, practicing different approaches enhances your problem-solving skills and builds a strong foundation for more advanced mathematical concepts. This seemingly simple question opens the door to a deeper understanding of fractions, their manipulation, and their application in various mathematical fields. Through practice and a firm grasp of these techniques, you'll confidently tackle similar fraction problems and build your mathematical prowess.
Latest Posts
Latest Posts
-
Swimming Coaching For Adults Near Me
Sep 12, 2025
-
How To Find The Perimeter Of Pentagon
Sep 12, 2025
-
How Long Does It Take For Sedimentary Rocks To Form
Sep 12, 2025
-
How Many 1 2 Cup In 1 4
Sep 12, 2025
-
How Long Is 10 Miles In Minutes Driving
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about How Many 1/6 Are In 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.