How Many 1/4 To Make 3/4
faraar
Sep 06, 2025 · 5 min read
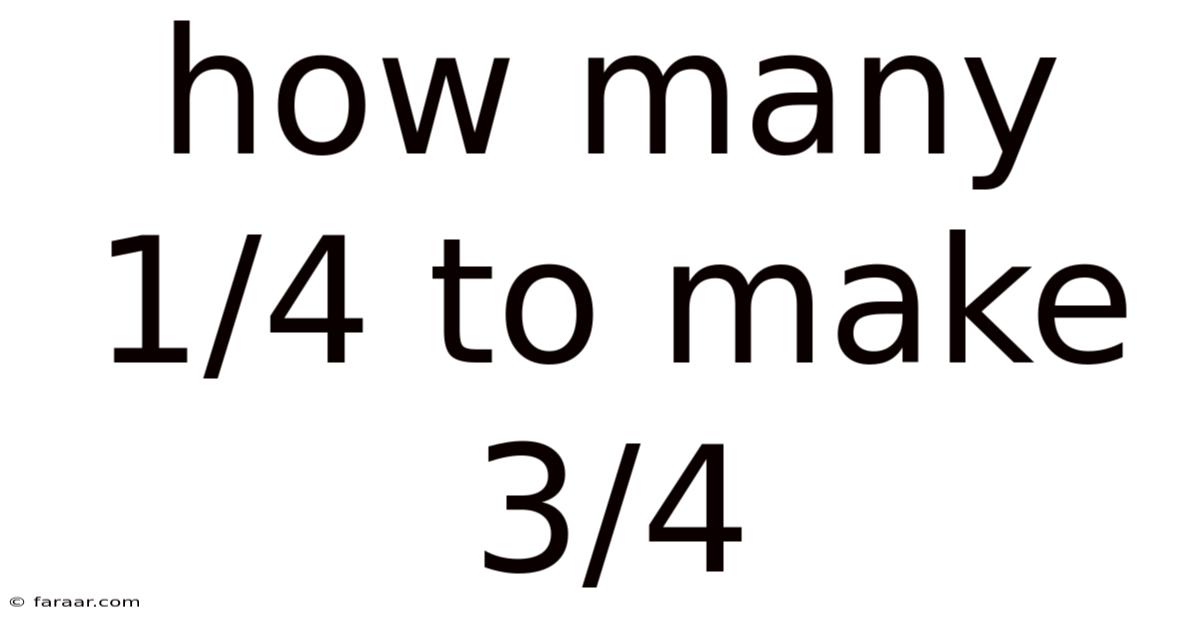
Table of Contents
How Many 1/4s Make 3/4? A Deep Dive into Fractions
Understanding fractions is a fundamental skill in mathematics, crucial for everyday life and more advanced studies. This article will explore the seemingly simple question, "How many 1/4s make 3/4?", providing a detailed explanation suitable for learners of all levels. We'll go beyond a simple answer, delving into the underlying concepts of fractions, providing practical examples, and addressing common misconceptions. This comprehensive guide aims to solidify your understanding of fractions and empower you to confidently tackle similar problems.
Introduction: Understanding Fractions
Before diving into the specific problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
For example, in the fraction 1/4, the denominator (4) means the whole is divided into four equal parts. The numerator (1) signifies that we're considering only one of those four parts. Similarly, 3/4 means three out of four equal parts.
How Many 1/4s Make 3/4? The Solution
The question "How many 1/4s make 3/4?" is essentially asking how many times 1/4 goes into 3/4. This can be solved in several ways:
1. Visual Representation:
Imagine a pizza cut into four equal slices. Each slice represents 1/4 of the pizza. If you have three slices, you have 3/4 of the pizza. Therefore, you can clearly see that three 1/4 slices make up 3/4 of the pizza.
2. Multiplication:
We can solve this using multiplication. We want to find the number 'x' such that x * (1/4) = 3/4. To solve for x, we can multiply both sides of the equation by 4:
4 * x * (1/4) = 4 * (3/4)
This simplifies to:
x = 3
Therefore, three 1/4s make 3/4.
3. Division:
Alternatively, we can approach this using division. We can divide 3/4 by 1/4:
(3/4) / (1/4) = (3/4) * (4/1) = 12/4 = 3
Again, this confirms that three 1/4s are equal to 3/4.
Expanding the Concept: Working with Different Fractions
The principle illustrated above extends to other fractions. Let's consider a few examples:
-
How many 1/8s make 3/8? Using the same logic as above, we can see that three 1/8s make 3/8.
-
How many 1/5s make 2/5? Two 1/5s make 2/5.
-
How many 1/10s make 7/10? Seven 1/10s make 7/10.
The pattern is clear: to find out how many fractions of the form 1/x make up a fraction of the form y/x, the answer is simply 'y'.
A Deeper Dive: The Mathematical Explanation
The solution hinges on the concept of equivalent fractions. Equivalent fractions represent the same proportion or value, even though they have different numerators and denominators. For instance, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions because they all represent one-half.
In our original problem, we're dealing with equivalent fractions of 3/4. We can express 3/4 as a sum of three 1/4s:
3/4 = 1/4 + 1/4 + 1/4
This clearly demonstrates that three 1/4s equal 3/4.
Practical Applications: Real-World Examples
Understanding fractions is vital in various real-world situations. Here are a few examples:
-
Cooking: Recipes often require fractional measurements of ingredients (e.g., 1/2 cup of flour, 3/4 teaspoon of salt). Knowing how to work with fractions ensures accurate measurements.
-
Measurement: In construction, carpentry, or engineering, accurate measurements are paramount. Fractions are frequently used to express precise dimensions.
-
Finance: Understanding fractions is essential for managing finances, calculating percentages, and understanding interest rates.
-
Data Analysis: In various fields, data is often presented in fractions or percentages. A firm understanding of fractions allows for accurate interpretation and analysis of this data.
Common Misconceptions and How to Avoid Them
While the concept seems straightforward, several common misconceptions can hinder a proper understanding of fractions. Let's address some of these:
-
Confusing Numerator and Denominator: Remember, the denominator represents the total number of parts, and the numerator represents the number of parts you're considering. Confusing these two leads to incorrect calculations.
-
Difficulty Visualizing Fractions: Using visual aids like pizza slices, pie charts, or fraction bars can significantly improve understanding and make the concept more intuitive.
-
Incorrectly Adding or Subtracting Fractions: Remember that you can only add or subtract fractions with the same denominator. If they have different denominators, you need to find a common denominator before performing the operation.
-
Misunderstanding Fraction Multiplication and Division: Multiplying fractions involves multiplying the numerators together and the denominators together. Dividing fractions involves inverting the second fraction (reciprocal) and then multiplying.
Frequently Asked Questions (FAQ)
Q: Can I solve this problem using decimals?
A: Yes, you can. 3/4 is equivalent to 0.75, and 1/4 is equivalent to 0.25. Dividing 0.75 by 0.25 also gives you 3.
Q: What if the question involved different fractions, for example, how many 2/5s make 6/5?
A: In this case, you would divide 6/5 by 2/5: (6/5) / (2/5) = (6/5) * (5/2) = 30/10 = 3. So three 2/5s make 6/5.
Q: Are there any online resources or tools that can help me practice working with fractions?
A: Yes, many websites and educational apps offer interactive exercises and tutorials on fractions. These resources can provide valuable practice and reinforcement.
Q: How does this relate to more advanced mathematical concepts?
A: Understanding fractions lays the foundation for more complex mathematical concepts, including algebra, calculus, and even advanced statistics. Mastering fractions is crucial for success in these areas.
Conclusion: Mastering Fractions for Future Success
This article thoroughly explored the question, "How many 1/4s make 3/4?", providing multiple approaches to solve the problem and emphasizing the underlying principles of fractions. We've gone beyond the simple answer, delving into the conceptual understanding, practical applications, and common misconceptions associated with working with fractions. By mastering the basics of fractions, you build a solid foundation for future success in mathematics and its various real-world applications. Remember to practice regularly using different methods and visualize the concepts to solidify your understanding. With consistent effort and the right approach, mastering fractions becomes achievable and even enjoyable!
Latest Posts
Latest Posts
-
What Is The Volume Of Water In A Graduated Cylinder
Sep 07, 2025
-
Which Of The Following Is True About Dna
Sep 07, 2025
-
Angles That Form A Linear Pair Add Up To
Sep 07, 2025
-
The Si Base Unit Of Mass Is The
Sep 07, 2025
-
Factoring Trinomials Where X2 Has A Coefficient
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about How Many 1/4 To Make 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.