How Many 1/3 Is In 3/4
faraar
Sep 19, 2025 · 5 min read
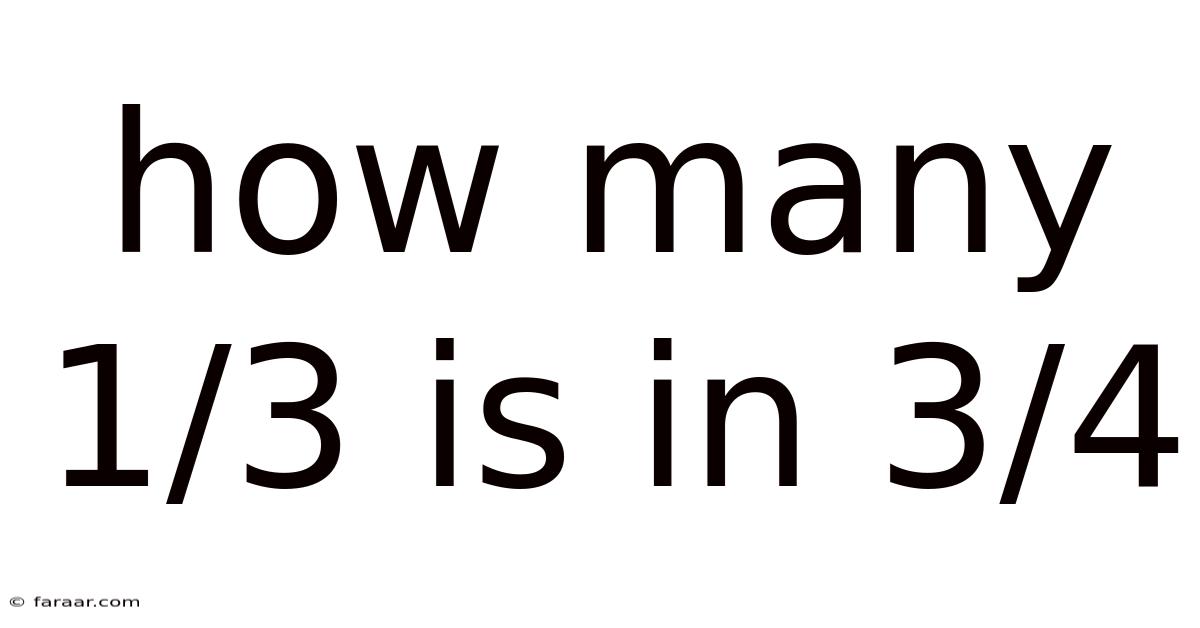
Table of Contents
How Many 1/3s are in 3/4? A Deep Dive into Fraction Division
This article will explore the seemingly simple question: "How many 1/3s are in 3/4?". While the answer might seem straightforward at first glance, delving into the process reveals fundamental concepts in fraction arithmetic, offering valuable insights into mathematical reasoning and problem-solving strategies. We'll cover the core calculation, explore different approaches, explain the underlying mathematical principles, and address common misconceptions. This comprehensive guide aims to equip you with a solid understanding of fraction division, applicable to various mathematical challenges.
Understanding the Problem: Fractions and Division
The question "How many 1/3s are in 3/4?" essentially asks us to divide 3/4 by 1/3. This is a classic example of fraction division, a topic crucial for understanding more complex mathematical concepts. Before tackling the solution, let's refresh our understanding of fractions.
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into.
Division, in its essence, asks: "How many times does one number fit into another?" When we divide fractions, we are essentially determining how many times one fractional part fits into another.
Method 1: The "Keep, Change, Flip" Method
This widely used method simplifies fraction division. It involves three steps:
- Keep: Keep the first fraction (the dividend) as it is: 3/4.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second fraction (the divisor) – find its reciprocal. The reciprocal of 1/3 is 3/1 (or simply 3).
Therefore, the problem becomes: (3/4) × (3/1) = 9/4.
This means there are 9/4 (or 2 1/4) 1/3s in 3/4.
Method 2: Visual Representation
Visualizing the problem can provide a clearer understanding. Imagine a circle representing a whole.
- 3/4: Divide the circle into four equal parts and shade three of them. This represents 3/4.
- 1/3: Now, consider another circle divided into three equal parts. One part represents 1/3.
The question is: How many times can we fit the 1/3 section (from the second circle) into the shaded 3/4 section (from the first circle)? This visual approach helps to intuitively grasp the concept, although it might not be practical for more complex fractions. To accurately determine the number of 1/3 sections that fit, the calculation (3/4) ÷ (1/3) = 9/4 is still necessary.
Method 3: Converting to Decimals
Another approach involves converting the fractions to decimals.
- 3/4 = 0.75
- 1/3 = 0.333... (a repeating decimal)
Dividing 0.75 by 0.333... gives approximately 2.25. This decimal representation aligns with our earlier answer of 9/4 (which is also equal to 2.25). However, using decimals can introduce rounding errors, especially with repeating decimals. Therefore, working with fractions directly is often preferred for accuracy.
The Mathematical Principle Behind Fraction Division
The "Keep, Change, Flip" method isn't just a trick; it's a consequence of the mathematical definition of division. Dividing by a fraction is the same as multiplying by its reciprocal. This can be proven algebraically.
Let's say we want to divide a/b by c/d. This can be written as:
(a/b) ÷ (c/d)
Using the definition of division (a ÷ b = a × (1/b)), we can rewrite this as:
(a/b) × (d/c) = (a × d) / (b × c)
Notice how this mirrors the "Keep, Change, Flip" method. We keep a/b, change division to multiplication, and flip c/d to d/c.
Addressing Common Misconceptions
A frequent error is simply dividing the numerators and denominators separately: (3 ÷ 1) / (4 ÷ 3) = 3/ (4/3) = 9/4. While this coincidentally leads to the correct answer in this specific case, it's not a valid method for general fraction division.
Another common mistake is to incorrectly flip both fractions. Remember, only the divisor (the second fraction) is flipped.
Expanding the Understanding: Applications and Further Exploration
Understanding fraction division extends beyond simple arithmetic. It's foundational to various mathematical concepts and real-world applications:
- Recipe scaling: Adjusting ingredient quantities in a recipe requires dividing or multiplying fractions.
- Measurement conversions: Converting units like inches to centimeters or liters to gallons involves fraction operations.
- Geometry: Calculating areas and volumes often involves fractional values.
- Algebra: Solving equations with fractions requires a solid understanding of fraction arithmetic.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Yes, most calculators can handle fraction division. However, understanding the underlying mathematical principles is crucial for problem-solving beyond simple calculations.
Q: Why is the "Keep, Change, Flip" method valid?
A: The method is a shortcut derived from the mathematical definition of division and the properties of reciprocals. It's a concise way to perform fraction division accurately.
Q: What if the fractions are mixed numbers (e.g., 2 1/2)?
A: Convert the mixed numbers into improper fractions before applying any of the methods described above. For example, 2 1/2 becomes 5/2.
Q: Are there other methods to solve this type of problem?
A: While the methods discussed are the most common and efficient, you could also use long division with decimals or find a common denominator before performing division. However, these methods are typically less straightforward.
Conclusion: Mastering Fraction Division
The question "How many 1/3s are in 3/4?" serves as an excellent example for understanding and mastering fraction division. By employing the "Keep, Change, Flip" method or visual representations, we determined that there are 9/4 (or 2 1/4) 1/3s in 3/4. This seemingly simple problem unveils fundamental mathematical concepts crucial for solving more complex problems in various fields. Remember to practice regularly, explore different approaches, and always strive for a deep understanding of the underlying principles to build a strong foundation in mathematics. Through consistent effort and a curious mindset, you can confidently navigate the world of fractions and conquer more challenging mathematical tasks.
Latest Posts
Latest Posts
-
Electric Guitar Lessons Near Me For Beginners
Sep 19, 2025
-
Distributive Property And Order Of Operations
Sep 19, 2025
-
Which Statement Describes A Chemical Reaction
Sep 19, 2025
-
How Many Cups Is 1 Pound Of Pecans
Sep 19, 2025
-
Give The Products Of The Reaction
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about How Many 1/3 Is In 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.