How Do You Graph Y 2 3x 1
faraar
Sep 21, 2025 · 7 min read
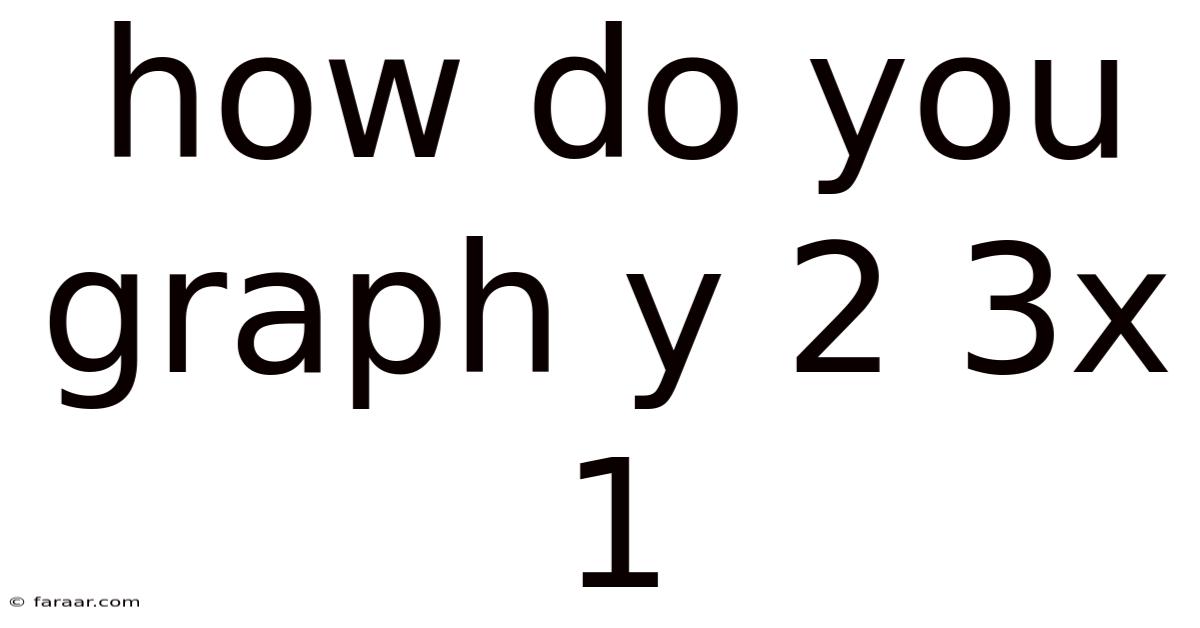
Table of Contents
How Do You Graph y = 2(3ˣ) + 1? An In-Depth Guide to Exponential Functions
Understanding how to graph exponential functions like y = 2(3ˣ) + 1 is crucial for anyone studying algebra, precalculus, or calculus. This equation represents an exponential growth function, a type of function that describes scenarios where a quantity increases at a constant percentage rate over time. This detailed guide will walk you through the process step-by-step, explaining the underlying principles and providing practical tips for accurate graphing. We'll cover everything from identifying key features to using different techniques for plotting the graph.
Understanding the Components of the Equation
Before we dive into graphing, let's break down the equation y = 2(3ˣ) + 1 and understand what each component means:
y: This represents the dependent variable, the output of the function. Its value depends on the value ofx.x: This represents the independent variable, the input of the function. We choose values forxand calculate the corresponding values ofy.3ˣ: This is the core of the exponential function. The base, 3, represents the constant multiplier, and the exponent,x, indicates how many times the base is multiplied by itself. For example, if x = 2, then 3ˣ = 3² = 9.2: This is the coefficient multiplying the exponential term. It vertically stretches the graph by a factor of 2. Each y-value will be twice as large as it would be without this coefficient.+1: This is the constant term, which represents a vertical shift. The entire graph is shifted upward by 1 unit.
Steps to Graph y = 2(3ˣ) + 1
Here's a step-by-step guide on how to graph the function y = 2(3ˣ) + 1:
1. Create a Table of Values:
The easiest way to graph any function is by plotting several points. Start by choosing a range of x-values. For exponential functions, it's helpful to include both positive and negative values, and zero. Let's choose x-values from -2 to 2:
| x | 3ˣ | 2(3ˣ) | y = 2(3ˣ) + 1 |
|---|---|---|---|
| -2 | 1/9 | 2/9 | 11/9 ≈ 1.22 |
| -1 | 1/3 | 2/3 | 5/3 ≈ 1.67 |
| 0 | 1 | 2 | 3 |
| 1 | 3 | 6 | 7 |
| 2 | 9 | 18 | 19 |
2. Plot the Points:
Using the table of values, plot each (x, y) coordinate on a Cartesian coordinate plane. Remember to label your axes (x and y) and choose appropriate scales for both axes to accommodate the range of your data.
3. Draw the Curve:
Exponential functions are characterized by their smooth, continuous curves. Connect the plotted points with a smooth curve. Do not simply connect the dots with straight lines. The curve should be gradually increasing, getting steeper as x increases. It will approach, but never quite reach, a horizontal asymptote.
4. Identify Key Features:
Once you've drawn the curve, identify and label the following key features:
- y-intercept: This is the point where the graph intersects the y-axis (where x = 0). In this case, the y-intercept is (0, 3).
- Horizontal Asymptote: This is a horizontal line that the graph approaches as x approaches negative infinity. Because of the +1, the horizontal asymptote for this function is y = 1. The graph will get increasingly closer to this line as x becomes more and more negative, but it will never actually touch it.
- Increasing or Decreasing: This function is increasing because as x increases, y also increases.
5. Interpret the Graph:
The graph visually represents the exponential growth of the function. You can use the graph to estimate the value of y for any given x, or vice versa. For example, you can visually see that when x is approximately 1.5, y is around 10.
Using a Graphing Calculator or Software
Graphing calculators (like TI-84) and graphing software (like Desmos or GeoGebra) provide an efficient way to graph functions. Simply input the equation y = 2(3ˣ) + 1 and the software will generate the graph automatically. These tools are invaluable for checking your hand-drawn graph and exploring the function's behavior over a wider range of x-values. They also allow for precise determination of key features like the y-intercept and the asymptote.
Further Exploration: Transformations of Exponential Functions
Understanding the graph of y = 2(3ˣ) + 1 provides a foundation for understanding transformations of exponential functions. The equation is a transformation of the basic exponential function y = 3ˣ. The 2 stretches the graph vertically, and the +1 shifts it vertically upwards. Consider these other transformations:
- Vertical Stretch/Compression: A coefficient greater than 1 (like the 2 in our example) stretches the graph vertically. A coefficient between 0 and 1 compresses it vertically.
- Vertical Shift: Adding a constant to the function (like the +1) shifts the graph vertically upwards. Subtracting a constant shifts it downwards.
- Horizontal Shift: Adding or subtracting a constant inside the exponent (e.g., y = 2(3ˣ⁻¹)+1) shifts the graph horizontally. Adding shifts it to the right, and subtracting shifts it to the left.
- Reflection: A negative coefficient reflects the graph across the x-axis, and a negative exponent reflects it across the y-axis.
By understanding these transformations, you can quickly sketch the graph of many different exponential functions without needing to create extensive tables of values.
The Scientific Explanation: Exponential Growth
The function y = 2(3ˣ) + 1 exemplifies exponential growth. This type of growth is characterized by a constant percentage increase over equal intervals. In this case, for every unit increase in x, the value of 3ˣ is multiplied by 3. This leads to increasingly rapid growth as x increases. Many real-world phenomena exhibit exponential growth, including population growth (under ideal conditions), compound interest, and the spread of certain diseases.
Frequently Asked Questions (FAQ)
Q: What is the domain of the function y = 2(3ˣ) + 1?
A: The domain of an exponential function is all real numbers. You can substitute any real number for x and get a corresponding real number for y.
Q: What is the range of the function y = 2(3ˣ) + 1?
A: The range of this function is (1, ∞). This means the y-values are greater than 1, but never actually reach 1 (due to the horizontal asymptote).
Q: How does changing the base (the 3) affect the graph?
A: A larger base results in faster growth. For example, if we changed the base to 4 (y = 2(4ˣ) + 1), the graph would increase much more steeply. A smaller base (but still greater than 1) would result in slower growth. If the base were between 0 and 1, the function would exhibit exponential decay (decreasing values).
Q: What if the equation was y = -2(3ˣ) + 1? How would that change the graph?
A: The negative coefficient (-2) would reflect the graph across the x-axis. The graph would start high, decrease, and approach a horizontal asymptote at y=1 from above.
Q: Can I use logarithms to solve for x if I know the value of y?
A: Yes. If you know the value of y, you can solve for x using logarithms. First, isolate the exponential term, then take the logarithm (usually base 10 or the natural logarithm) of both sides of the equation.
Conclusion
Graphing exponential functions like y = 2(3ˣ) + 1 might seem daunting at first, but by breaking down the equation, creating a table of values, plotting the points, and understanding the underlying principles of exponential growth, the process becomes manageable and even insightful. Remember to identify key features like the y-intercept, horizontal asymptote, and the overall increasing or decreasing nature of the function. Using graphing tools can help verify your work and explore the function's behavior more extensively. Mastering this skill provides a strong foundation for further studies in mathematics and its applications to real-world problems. The ability to visualize and interpret exponential functions is a valuable asset in many fields, from finance and biology to engineering and computer science.
Latest Posts
Latest Posts
-
How To Calculate Turnover Number Of Enzyme
Sep 21, 2025
-
Write The Perimeter Of The Rectangle As A Simplified Expression
Sep 21, 2025
-
Design A Positive Ion With A Charge Of 2
Sep 21, 2025
-
Ap English Language And Composition Tutor
Sep 21, 2025
-
Potassium Hydroxide Sulfuric Acid Balanced Equation
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about How Do You Graph Y 2 3x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.