Graph Of Y 1 2x 3
faraar
Sep 11, 2025 · 6 min read
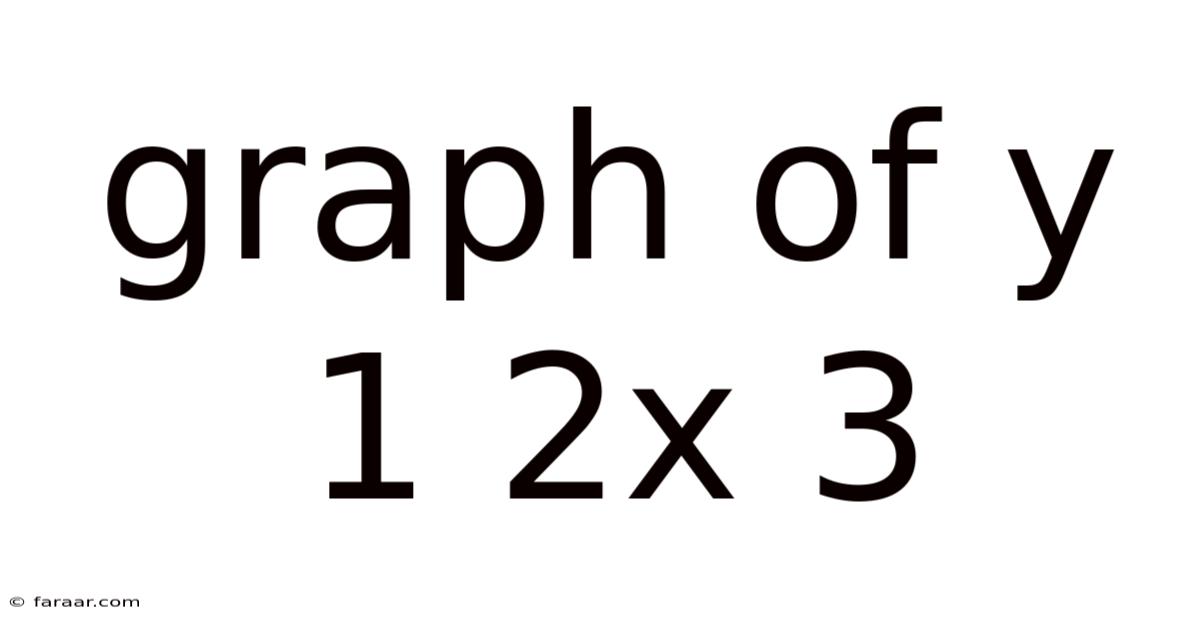
Table of Contents
Unveiling the Secrets of the Graph y = 1/(2x + 3)
Understanding the graph of y = 1/(2x + 3) involves exploring several key aspects of its behavior: its domain and range, asymptotes, intercepts, and overall shape. This seemingly simple equation reveals a rich tapestry of mathematical concepts crucial for a strong foundation in algebra and calculus. This article will guide you through a comprehensive analysis of this function, explaining its properties in a clear and accessible manner. We'll uncover the secrets behind its shape, its limitations, and its behavior as x approaches certain values.
Understanding the Basics: Domain and Range
Before diving into the complexities of the graph, let's first define the domain and range of the function y = 1/(2x + 3).
-
Domain: The domain represents all possible input values (x-values) for which the function is defined. In this case, the function is undefined when the denominator is zero. Therefore, we set the denominator equal to zero and solve for x:
2x + 3 = 0 2x = -3 x = -3/2
This means that the function is undefined at x = -3/2. Consequently, the domain of the function is all real numbers except x = -3/2. We can express this in interval notation as: (-∞, -3/2) U (-3/2, ∞).
- Range: The range represents all possible output values (y-values) the function can produce. Since the numerator is a constant (1), the function can take on any value except 0. As x approaches -3/2, the denominator approaches zero, and the function approaches positive or negative infinity depending on whether x approaches -3/2 from the left or the right. Therefore, the range of the function is all real numbers except y = 0. In interval notation, this is: (-∞, 0) U (0, ∞).
Asymptotes: The Invisible Boundaries
The graph of y = 1/(2x + 3) exhibits two types of asymptotes: vertical and horizontal.
-
Vertical Asymptote: A vertical asymptote occurs where the function approaches infinity or negative infinity as x approaches a certain value. In our case, this occurs at x = -3/2, as we've already established. The graph will approach this vertical line but never actually touch it. This is because the function is undefined at x = -3/2.
-
Horizontal Asymptote: A horizontal asymptote describes the behavior of the function as x approaches positive or negative infinity. To find the horizontal asymptote, we examine the limit of the function as x approaches infinity:
lim (x→∞) 1/(2x + 3) = 0
Similarly, as x approaches negative infinity:
lim (x→-∞) 1/(2x + 3) = 0
This tells us that the function approaches 0 as x becomes very large (positive or negative). Therefore, the horizontal asymptote is y = 0. The graph will get arbitrarily close to this horizontal line but never actually touch it.
Intercepts: Where the Graph Crosses the Axes
-
x-intercept: The x-intercept is the point where the graph crosses the x-axis (where y = 0). However, since the range of the function excludes y = 0, there is no x-intercept.
-
y-intercept: The y-intercept is the point where the graph crosses the y-axis (where x = 0). To find this, we substitute x = 0 into the equation:
y = 1/(2(0) + 3) = 1/3
Therefore, the y-intercept is (0, 1/3).
Sketching the Graph: Bringing it All Together
Now that we've identified the key features – domain, range, asymptotes, and intercepts – we can sketch the graph.
-
Draw the asymptotes: Begin by drawing the vertical asymptote at x = -3/2 and the horizontal asymptote at y = 0. These lines act as guides for the graph.
-
Plot the y-intercept: Mark the point (0, 1/3) on the graph.
-
Consider the behavior near the asymptotes: As x approaches -3/2 from the left (values slightly less than -3/2), the denominator becomes a small negative number, resulting in a large negative y-value. As x approaches -3/2 from the right (values slightly greater than -3/2), the denominator becomes a small positive number, resulting in a large positive y-value.
-
Sketch the curves: Based on the behavior near the asymptotes and the y-intercept, sketch two separate curves. One curve will be in the region x < -3/2, approaching the asymptotes but never touching them. The other curve will be in the region x > -3/2, also approaching the asymptotes.
A Deeper Dive: Transformations and the Parent Function
Understanding the graph of y = 1/(2x + 3) can be simplified by relating it to its parent function, y = 1/x. This parent function is a hyperbola with branches in the first and third quadrants. The given equation is a transformation of this parent function.
Let's break down the transformations:
-
Horizontal Shift: The "+3" in the denominator indicates a horizontal shift of -3/2 units (to the left). This shifts the vertical asymptote from x = 0 (in the parent function) to x = -3/2.
-
Horizontal Compression: The "2" in the denominator represents a horizontal compression by a factor of 1/2. This makes the graph narrower than the parent function.
There is no vertical stretching or shifting in this particular case.
Analyzing the Function's Behavior: Limits and Derivatives (Advanced)
For those with a background in calculus, we can further analyze the function's behavior using limits and derivatives.
-
Limits: We've already used limits to find the horizontal asymptote. We can also use limits to analyze the behavior near the vertical asymptote:
lim (x→(-3/2)⁻) 1/(2x + 3) = -∞ lim (x→(-3/2)⁺) 1/(2x + 3) = ∞
These limits confirm the behavior we observed when sketching the graph.
- Derivatives: The first derivative of the function provides information about its slope and increasing/decreasing intervals. The second derivative gives information about concavity. Calculating these derivatives and analyzing their signs can offer a more rigorous understanding of the graph's shape. However, this is beyond the scope of a basic introduction and requires knowledge of calculus.
Frequently Asked Questions (FAQ)
Q: What is the significance of the vertical asymptote?
A: The vertical asymptote at x = -3/2 represents a value where the function is undefined. The function approaches positive or negative infinity as x approaches this value, indicating a discontinuity.
Q: Can the graph ever touch the asymptotes?
A: No, the graph will approach the asymptotes arbitrarily close but will never actually touch or cross them.
Q: How does changing the coefficients in the equation affect the graph?
A: Changing the coefficient of x in the denominator will affect the horizontal compression/stretching and the position of the vertical asymptote. Changing the constant term in the denominator will affect the horizontal shift. The numerator, if it were a constant other than 1, would affect the vertical stretching.
Conclusion: A Comprehensive Understanding
The graph of y = 1/(2x + 3) serves as a valuable example illustrating key concepts in function analysis. Understanding its domain, range, asymptotes, intercepts, and transformations provides a strong foundation for analyzing more complex functions. By breaking down the equation and examining its behavior, we've gained a thorough understanding of this seemingly simple yet insightful mathematical representation. This detailed exploration reinforces the importance of visualizing mathematical relationships and highlights the power of analytical tools in understanding function behavior. The principles discussed here are applicable to a wide range of functions, making this analysis a crucial stepping stone in your mathematical journey.
Latest Posts
Latest Posts
-
Density Of Water In Gm Cc
Sep 11, 2025
-
How To Find Zeros Of Polynomial Functions
Sep 11, 2025
-
Find Any Domain Restrictions On The Given Rational Equation
Sep 11, 2025
-
10 Gallons To 24 Gallons Find The Percent Of Change
Sep 11, 2025
-
Average Rate Of Change Instantaneous Rate Of Change
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Graph Of Y 1 2x 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.